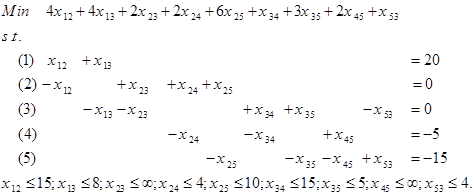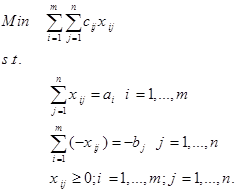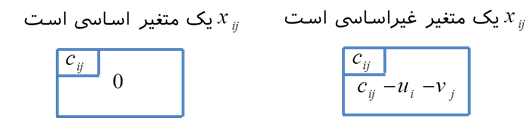مسئله حمل و نقل
برای دانلود خلاصه آموزش مسئله حمل و نقل لطفا ایمیل خود را وارد کنید تا این آموزش برای شما ارسال شود. این آموزش شامل فیلم، جزوه، پادکست و فایل ارایه است.
درس 5: مسئله حمل و نقل
تهیه شده توسط گروه بهینهیاب
تا کنون به بررسی مسئله برنامه ریزی خطی به صورت کلی پرداختیم. در این بخش به بررسی انواع خاص مسئله برنامه ریزی خطی خواهیم پرداخت. در این بخش ابتدا به بررسی مدل عمومی جریان در شبکه پرداختیم. سپس به بررسی مدل های خاص جریان در شبکه مانند مسئله حمل و نقل، مسیر بحرانی، مسئله جریان بیشین و مسئله کوتاه ترین مسیر خواهیم پرداخت.
مسئله عمومی جریان در شبکه
در مسئله جریان در شبکه، به دنبال توزیع محصول همگن از کارخانه (مبادی) به بازار فروش (مقاصد) هستیم. فرض کنید تعداد کل واحدهای محصول تولید شده در هر کارخانه و تعداد کل محصول مورد نیاز معلوم است. همچنین لازم نیست که محصول مستقیما به مقاصد ارسال شود بلکه امکان دارد که از طریق سایر نقاط به مراکز توزیع ارسال شود. به علاوه، قیدهای ظرفیت بعضی از خطوط حملونقل را محدود میکند. هدف در این مسئله کمینه کردن هزینه حمل محصولها است.
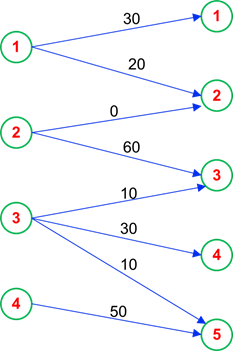
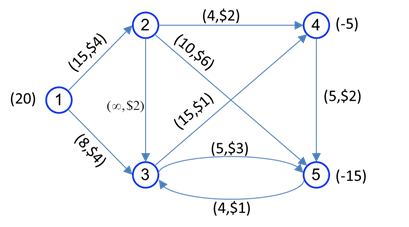
مثال عددی از مسئله جریان در شبکه در شکل زیر را در نظر بگیرید. گرهها با دایره های شماره دار و کمانها با کمانها نشان داده شده اند. کمانها جهت دار هستند. مثلا مواد میتوانند از گره 1 به گره 2 فرستاده شود ولی از گره 2 به گره 1 این امکان وجود ندارد. کمان از گره i به گره j را به صورت i-j نشان میدهیم.
در مسئله جریان در شبکه، هدف یافتن الگوی جریان با هزینه کمینه است. برای تبدیل مسئله به صورت برنامهریزی خطی، فرض کنید:
xij : تعداد واحدهای حمل شده از گره i به گره j با استفاده از کمان i-j است.
مدل برنامهریزی خطی جریان در شبکه به صورت زیر ارایه میشود.
معادلات 1 تا 5، معادلات توازن جریان در شبکه است. برای مثال معادله جریان تعادل در گره 1 به صورت زیر میشود.
معادله فوق این نکته را بیان میکند که جریان خروجی از گره 1 ( x12+x13 )، باید برابر با میزان عرضه گره 1 (20) باشد. معادله توازن در گره 2، بیان میکند که جریان ورودی به گره 2 ( x12 ) برابر جریان خروجی از گره 2 ( x24+x25+x23) است.
مدل جریان در شبکه دارای ساختار خاصی است که برای ارایه دستور حل از آن مورد استفاده قرار میگیرد. متغیرهای جریان xij در معادلات توازن فقط ضریب 0، 1+ و 1- اخذ میکنند. به علاوه دقیقا در دو معادله توازن ظاهر میشوند: یک بار با ضریب 1+ مربوط به گرهای که از آن سرچشمه میگیرند و 1- مربوطه به گرهای که به آن وارد میشوند. با توجه به موارد فوق، فرم عمومی مسئله کمترین جریان در شبکه را به n گره به صورت زیر بیان میشود.
مدل فوق، مدل عمومی مسئله جریان کمینه در شبکه است. برای شرایط خاص، مدل فوق قابل تبدیل به فرم های ساده تری است که در ادامه برخی از این مدل های خاص را بیان میکنیم.
مسئله حمل و نقل
مسئله حمل و نقل نوعی مدل جریان در شبکه است که در آن نقطه واسط (مانند گره های 2 و 3 در شکل فرم عمومی) وجود ندارد. برای بیان فرم ریاضی مسئله حملونقل، پارامترهای زیر تعریف میشود.
ai : تعداد واحدهای موجود در منبع i-ام (i=1,…,m)
bj : تعداد واحدهای مورد نیاز در مقصد j-ام (j=1,…,n)
cij : هزینه حملونقل هر واحد از منبع i-ام به مقصد j -ام ( i=1,…,m و j=1,…,n )
فرض میشود که مجموع کل تعداد واحدهای موجود در منابع با تعداد واحدهای مورد نیاز در مقاصد برابر باشند، یعنی:
اگر فرض فوق برقرار نباشد، با اعمال تغییراتی میتوان فرض فوق را برقرار کرد که بعدا به آن خواهیم پرداخت.
اگر xij برابر تعداد واحدهایی که از منبع i به مقصد j حمل میشود در نظر گرفته شود، آنگاه مسئله حمل و نقل را میتوان به صورت زیر فرمول بندی کرد:
مثال: محصولات یک شرکت بزرگ کنسرو سازی در سه کارخانه تولید میشود و به وسیله کامیون به چهار انبار مستقر میشوند. چون هزینه انتقال مبلغ قابل توجهی است، لذا مدیریت به دنبال کمینه کردن این هزینهها است. اطلاعات مربوط به هزینه حمل در جدول زیر آمده است:
مدل برنامهریزی خطی مسئله فوق به صورت زیر بیان میشود.
ارایه دستور حل سیمپلکس برای مسئله حمل و نقل
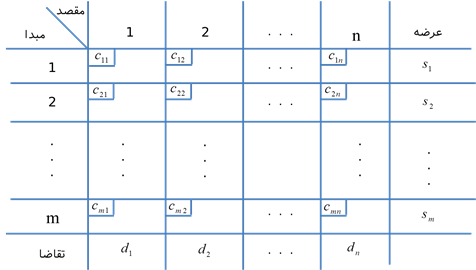
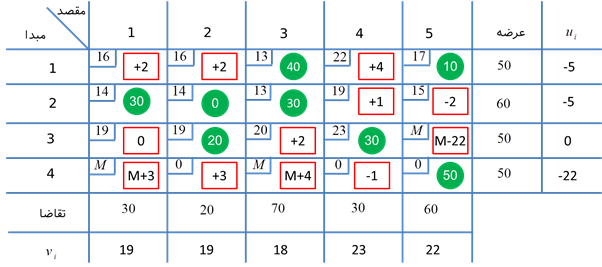
از آنجایی که مسئله حمل و نقل حالتی خاص از مسئله برنامه ریزی خطی است، لذا میتوان با استفاده از روش سیمپلکس حل کرد. ولی از آن جایی که ساختار مسئله حمل و نقل خاص است میتوان از روش ساده تری جواب بهینه را بدست آورد. به جای این که از جدول سیمپلکس برای یافتن جواب بهینه استفاده کرد، میتوان از جدول زیر ذخیره اطلاعات جدول سیمپلکس در مسئله حمل و نقل استفاده کرد.
در صورتی که متغیر اساسی یا غیراساسی باشد، اطلاعات هر خانه به صورت زیر تعیین میشود.
قدم ابتدایی:
در این قدم یک جواب اساسی موجه بدست میآوریم. در مسئله حمل و نقل روش های مختلفی برای تولید جواب اولیه وجود دارد که در ادامه دو روش معروف ارایه میگردد.
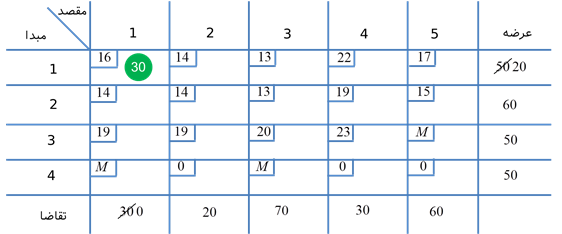
روش گوشه شمال غربی (north west corner rule):
ابتدا متغیر x11 را انتخاب کنید که به عنوان متغیر اساسی در نظر میگیریم. در ادامه اگر xij متغیر اساسی باشد و حال چنانچه عرضه مبدا i تمام نشده باشد، متغیر xij+1 و در غیر این صورت متغیر xi+1j را به عنوان متغیر اساسی انتخاب میکنیم.
برای مثال جدول سیمپلکس زیر را در نظر بگیرید. با توجه به این قاعده جواب اساسی اولیه به صورت زیر تولید میشود.
جواب اساسی اولیه به صورت زیر است.
روش تخمین فوگل (Vogel’s Approximation)
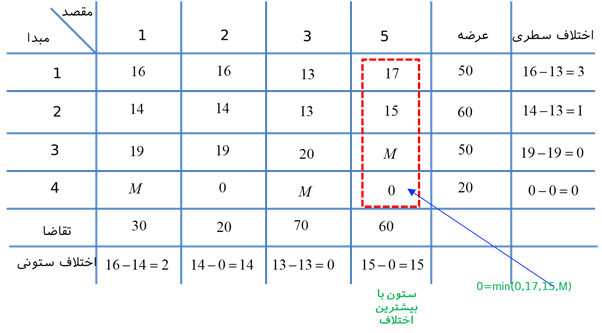
روش قبلی هزینه را در نظر نمیگیرد، اما روش هایی که هزینه را در نظر نمیگیرد میتواند به جواب های منجر شود که هزینه کل بسیار زیاد شود. روش تخمین فوگل برای رفع این مشکل پیشنهاد شده است و آنقدر اثر بخش است که گاهی برای بدست آوردن جواب بهینه تقریبی مورد استفاده قرار میگیرد. روش تخمین فوگل به این صورت عمل میکند که به ازای هر سطر یا ستونی که هنوز تحت بررسی است، تفاوت بین کوچکترین و ما قبل کوچکترین هزینه واحد cij محاسبه کنید. در سطر یا ستونی که تفاوت آن از همه بزرگتر است، متغیر که هنوز حذف نشده است و هزینه واحد ان از همه کمتر است را انتخاب میکند.
برای روشن شدن موضوع، جواب اساسی اولیه جدول سیمپلکس زیر را با استفاده از روش تخمین فوگل بدست آورید.
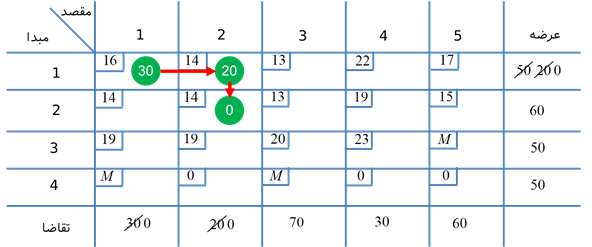
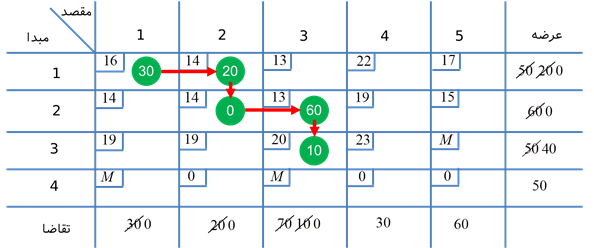
تکرار 1:
ستون 4 حذف میشود و x44 = 30 در نظر گرفته میشود.
تکرار 2:
سطر 4 حذف میشود و x45 = 20 در نظر گرفته میشود.
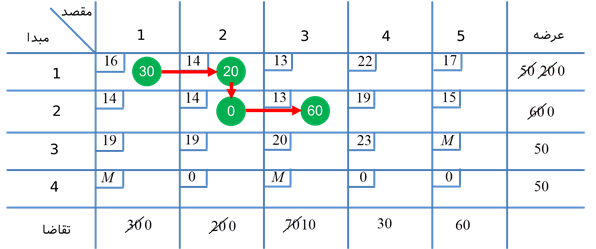
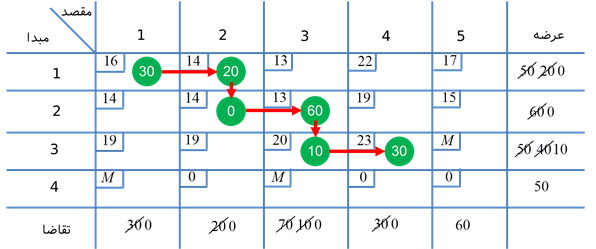
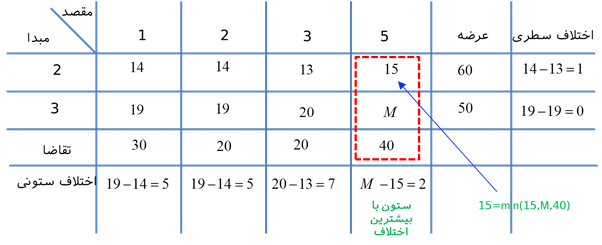
تکرار 3:
سطر 1 حذف میشود و x13 = 50 در نظر گرفته میشود.
تکرار 4:
ستون 5 حذف میشود و x25 = 40 در نظر گرفته میشود.
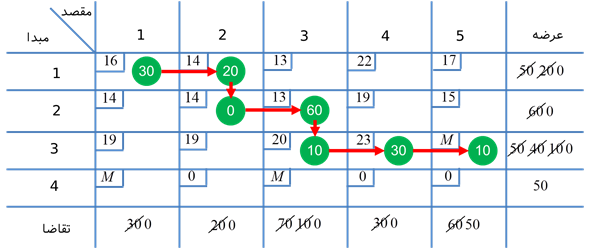
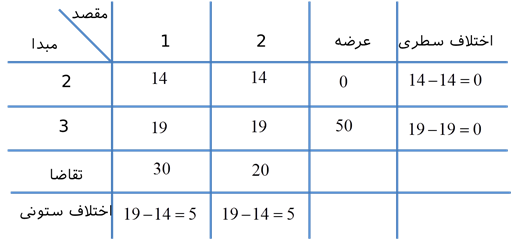
تکرار 5:
ستون 3 حذف میشود و x23 = 20 در نظر گرفته میشود.
تکرار 6:
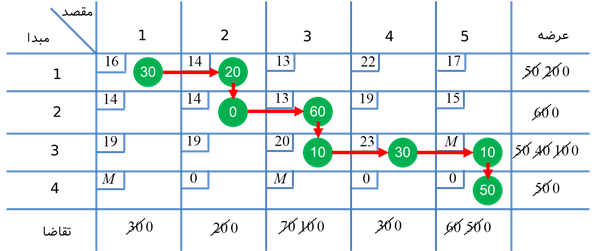
جدول فوق، جدول نهایی است و داریم: x33 = 0 , x32 = 20 , x31 = 30. لذا جواب اساسی اولیه برای مسئله حمل و نقل به صورت زیر میشود.
دستور توقف
هدف دستور توقف، آزمون بهینگی جواب اساسی موجه فعلی است. یک جواب اساسی موجه بهینه است اگر و فقط اگر به ازای کلیه متغیرهای غیر اساسی xij رابطه زیر برقرار باشد.
0≤ cij-ui-vj
برای کنترل شرایط بالا باید مقدار ui و vj را محاسبه کرد. در صورتی که متغیر xij اساسی باشد آنگاه cij-ui-vj = 0 خواهد بود. از حل دستگاه معادلات برای متغیرهای اساسی میتوان ui و vj را محاسبه کرد. به دلیل این که تعداد معادلات یک واحد از تعداد متغیرها کمتر است. لذا میتوان برای یافتن جواب این دستگاه معادلات، یکی از متغیرها را مساوی با مقدار دلخواه گرفت و با توجه به ساختار ساده دستگاه معادلات، مقدار سایر متغیرها را بدست آورد.
برای نشان دادن این موضوع، اگر متغیرهای اساسی x31، x32 ، x34 ، x21 ، x23 ، x13 ، x15 و x45 باشند، آنگاه داریم:
اگر u3 = 0 قرار دهیم (چون u3 بیشترین حضور در معادلات را دارد)، مقادیر سایر متغیرها به صورت زیر بدست میآید.
با در اختیار داشتن مقدار متغیرهای همزاد میتوان شرایط بهینگی را کنترل کرد.
قدم تکراری
در این قدم، متغیر اساسی ورودی و متغیر اساسی خروجی را تشخیص میدهیم. در روش سیمپلکس مسئله حمل و نقل، متغیری که منفی ترین مقدار cij-ui-vj را داشته باشد، به عنوان متغیر اساسی ورودی در نظر میگیریم. بر اساس مقادیر و از مرحله قبل، جدول سیمپلکس مسئله حمل و نقل به صورت زیر میشود.
در جدول فوق، متغیر x25 دارای کمترین مقدار cij-ui-vj است و به عنوان متغیر ورودی استفاده میشود. برای یافتن متغیر اساسی خروجی از پایه یک سری کارهای زنجیره ای نسبتا ساده به صورت زیر انجام میشود.
در شکل فوق، مقدار θ تا اندازهای باید افزایش یابد که هزینه کمان منفی نشود لذا خواهیم داشت:
قبل از حل چند مثال، بیان رسمی روش سیمپلکس برای مسئله حمل و نقل را ادامه خواهیم داشت:
قدم ابتدایی:
جواب اساسی موجه ابتدایی را با استفاده از یکی از دو روش، روش شمال غربی یا روش تخمین فوگل بدست آورید.
دستور توقف:
دستگاه معادله cij = ui + vj را برای متغیرهای اساسی حل کنید. مقدار متغیرهای همزاد ui و vj را بدست آورید. در صورتی که برای تمامی متغیرهای غیراساسی رابطه زیر برقرار باشد، آنگاه جواب اساسی موجه فعلی بهینه است:
0≤ cij-ui-vj
در غیر این صورت به قدم تکراری بروید.
قدم تکراری:
قسمت 1: متغیر غیر اساسی xij که منفی ترین مقدار cij – ui – vj را به عنوان متغیر اساسی ورودی در نظر بگیرید.
قسمت 2: متغیر اساسی خروجی را بر اساس عکس العمل های زنجیره ای تعیین کنید.
قسمت 3: جواب اساسی موجه جدید را مشخص کنید.
برو به قدم توقف.