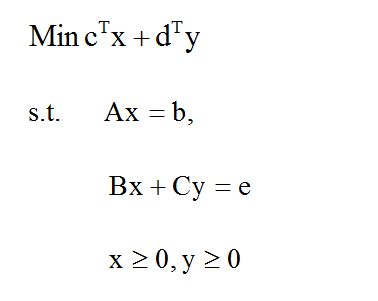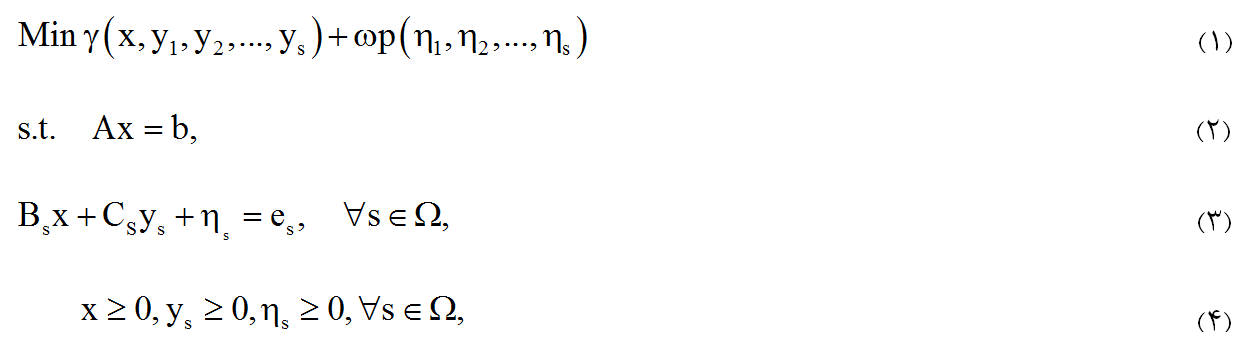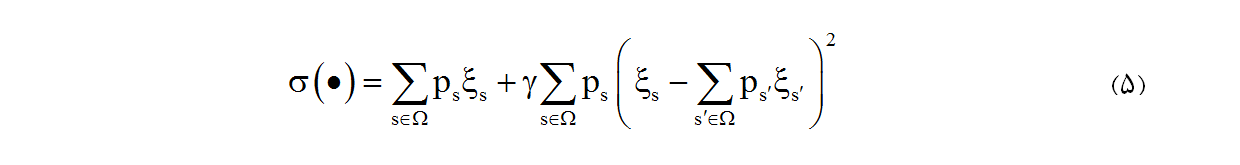برای دانلود خلاصه آموزش بهینه سازی استوار لطفا ایمیل خود را وارد کنید تا این آموزش برای شما ارسال شود. این آموزش شامل فیلم، جزوه، پادکست و فایل ارایه است.
دانلود بسته طلایی آموزش بهینه سازی استوار و حل تمرین های تشریحی
درس 29: بهینه سازی استوار
تهیه شده توسط گروه بهینه یاب
آ
مقدمه
در برنامهریزی ریاضی معمولا مسائل با پیش فرض قطعی بودن داده ها مدل سازی و حل می شوند. پیش فرض اصلی برنامهریزی ریاضی در شرایط اطمینان، توسعه مدل بر اساس داده های معین و برابر با مقادیر اسمی است؛ در این گونه مدل ها اثر عدم اطمینان داده ها در کیفیت و امکان پذیری جواب ها تأثیری ندارد، در نتیجه در مسائل دنیای واقعی ممکن است با تغییر یکی از داده ها، تعداد زیادی از محدودیت ها نقض و جواب به دست آمده غیر بهینه یا حتی غیر ممکن شود. از این رو، چالش اصلی در این گونه مسائل، رسیدن به پاسخ مسئله است که در مقابل عدم اطمینان داده ها استوار باشد؛ به اصطلاح این جواب ها را جواب های استوار و این دسته از مسائل بهینه سازی ها را مسائل بهینه سازی استوار می نامند. نظریه برنامهریزی یا بهینه سازی استوار روش ریسک گریزی را برای مواجهه با عدم اطمینان فراهم می سازد.
استواری به این مفهوم است که خروجی مدل نباید حساسیت زیادی به مقادیر دقیق پارامترهای ورودی داشته باشد. اهمیت این ویژگی در مدل ها باعث شده است که کاربرد بحث استواری در سال های اخیر در حوزه های مختلف با رشد فزاینده ای همراه شود. برنامهریزی استوار در مباحث زمان بندی، مدیریت کیفیت، تخصیص منابع، طراحی سیستم های تولیدی، مدیریت زنجیره تأمین، تدوین استراتژی، حمل و نقل و مسائل مالی چشمگیر شده است. به طور کلی می توان مدل های معرفی شده در زمینه برنامهریزی استوار را به دو فهرست کلی تقسیم بندی کرد.
دسته اول مدل هایی است که مبتنی بر سناریوهای گسسته تعریف می شود. در این مدل ها مقدار تابع هدف در هر یک از سناریوها باید اختلاف کمی با یکدیگر داشته باشند.
دسته دوم نیز بر اساس مفهوم مجموعه های عدم اطمینان و مبتنی بر نوسان پارامترها در یک بازه است. در این مدل ها، عدم اطمینان در شکل مجموعه های عدم اطمینان کران دار مدل سازی می شود و هدف به دست آوردن جواب است که نسبت به تقریبا تمام پارامترهای عدم اطمینان حساسیت نداشته باشد. در واقع، پارامترهای پیوسته را می توان با رویکرد برنامهریزی استوار در فواصل مشخصی محدود کرد و عدم اطمینان را در یک مجموعه مناسب جای داد.
جواب حاصل از این مدل جوابی است که نسبت به تغییرات داده های ورودی کمتر حساس است. در این نظریه یک راه حل برای یک مسئله بهینه سازی در صورتی استوار است که هم استوار موجه (استواری مدل) و هم استوار بهینه (استواری جواب) باشد.
استواری موجه به این معنی است که راه حل باید در محدودیت های مسئله برای تقریبا تمامی سناریوها موجه باقی بماند؛ برای این منظور در روش مطالعه مالوی و همکاران، ناموجه بودن جواب با یک تابع جریمه اندازه گیری می شود. موجه بودن جواب مستلزم این است که تابع جریمه دارای مقدار پایینی باشد.
استواری بهینگی نیز به این معنی است که مقدار تابع هدف برای جواب مسئله باید نزدیک به مقدار بهینه باقی بماند یا دارای حداقل انحرافات نامطلوب از مقدار بهینه برای هر یک از مقادیر سناریوها باشد.
در تابع هدف مدل مالوی و همکاران برای استواری مدل و استواری جواب دارای جریمه هستیم که با توجه به ترجیح مدل ساز به هر یک از این جريمه ها وزن اختصاص می دهیم. روشن است که در این مدل، با توجه به ترجیحات تصمیم گیرنده، بین استواری جواب و استواری مدل باید تبادل صورت گیرد. نحوه فرموله سازی مدل بهینه سازی استوار مالوی و همکاران در ادامه آورده شده است.
مدل برنامهریزی خطی با پارامترهای تصادفی زیر را در نظر بگیرید:
متغیر x برداری از متغیرهای طراحی و متغیر y نیز برداری از متغیرهای کنترل است. پارامترهای A، B و C ماتریس پارامترها و b و e نیز بردار پارامترها هستند. همچنین A و b مشخص و C ,B و e نادقیق هستند.
تحقق هر مقدار برای پارامتر نادقیق یک سناریو نامیده می شود، که با s نشان داده و احتمال آن با ps آورده می شود ( مجموع ps برای تمامی s ها برابر یک است). برای نمایش مجموعه سناریوها از (Ω={1,2,..,S استفاده می کنیم. ضرایب نادقیق B، C و e را نیز به صورت Cs، Bs و es برای هر سناریو s∈S نشان می دهیم. همچنین، متغیر کنترل y نیز که در زمان تحقق یک سناریو در معرض تعدیل قرار می گیرد، به صورت ys برای سناریو s نشان داده می شود. مدل بهینه سازی استوار تصادفی به صورت زیر فرموله می شود:
به دلیل نادقیق بودن پارامترها، مدل ممکن است برای برخی سناریوها ناموجه باشد. مجموعه {η1,…,ηS} شامل بردار های خطا است که اندازه ناموجه بودن در محدودیت های کنترل (3) برای سناریو s را اندازه گیری می کند. در صورت موجه بودن مدل برای سناریوی s برای ηs برابر با صفر خواهد بود؛ در غیر این صورت، ηs در محدودیت (3) مقدار مثبتی خواهد بود. در مدل بالا، تابع هدف مدل اول (ξ=cTx+dTy) که می تواند تابع سود یا هزینه باشد، تبدیل به متغیر تصادفی به صورت (ξs=cTx+dsTys) می شود که متوسط آن به ازای سناریوها، سود یا هزینه مورد انتظار نامیده می شود.
در مدل بالا، تابع هدف دارای دو قسمت شامل استواری جواب و استواری مدل است که وزن قسمت اول با γ (گاما) و وزن قسمت دوم با ω (امگا) مشخص می شود.
در قسمت اول که استواری جواب را در نظر می گیرد، از ξs برای نمایش تابع هزینه یا سود (f(x,ys استفاده می کنیم. از این رو،(ξs = f(x,ys را برای سناریو s داریم. واریانس یا بزرگ برای متغیر تصادفی به معنی بالا بودن ریسک این جواب خواهد بود. در این صورت، یک تغییر کوچک در مقدار پارامترهای نادقیق مدل می تواند باعث یک تغییر بزرگ در مقدار تابع هدف شود. برای این قسمت، مالوی و همکاران از رابطه زیر استفاده کردند:
γ وزن تغییر پذیری جواب را نشان می دهد. در این عبارت، با عبارت درجه دوم نیاز به عملیات محاسباتی زیادی داریم. برای حل این مشكل، از قدر مطلق انحرافات به جای عبارت بالا می توان استفاده کرد که به صورت زیر بازنویسی می شود:
با توجه به غیر خطی بودن فرم قدر مطلق انحرافات، می توان با معرفی دو متغیر انحرافی غیر منفی از فرم غیر خطی را به فرم خطی تبدیل کرد و به جای حداقل سازی قدر مطلق انحرافات، این دو متغیر را با در نظر گرفتن محدودیت های اصلی و محدودیت های اضافی، حداقل ساخت. این محدودیت اضافی باعث می شود اختلاف درون قدر مطلق مقدار مثبتی بگیرد. بر این اساس، مسئله برنامهریزی غیر خطی بالا به صورت خطی بازنویسی می شود:
به زعم یو و لی (۲۰۰۰)، در روش خطی سازی بالا، با معرفی متغیرهای انحرافی غیر منفی، محدودیت های زیادی به مدل تحمیل می شود. برای این منظور، يو و لی از یک روش کارا برای خطی سازی فرم قدر مطلق انحرافات به صورت زیر استفاده کرده اند:
در قسمت دوم، از تابع جريمه ()ωp، برای دادن جریمه به ناموجه بودن مدل استفاده می شود که استواری مدل را اندازه گیری می کند. ω وزن غير موجه بودن مدل را نشان می دهد و با پارامتر γ تبادل بين استواری جواب و مدل را کنترل می کند. در مسئله ای که در ادامه آورده خواهد شد، ηs که ناموجه بودن مدل را نشان می دهد، تقاضای برآورده نشده در سناریو s خواهد بود. تابع جریمه، مقدار مورد انتظار بردار خطا ηs خواهد بود که به صورت زیر نشان داده می شود:
در نهایت، مدل برنامهریزی استوار تصادفی به صورت زیر فرموله می شود:
مبانی مدل سازی بهینه سازی استوار
نظریه بهینه سازی استوار چهارچوبی را برای مواجهه با عدم اطمینان پارامترها در مسائل بهینه سازی فراهم می سازد، به طوری که می توان جواب بهینه را برای وقوع عدم اطمینان در یک مجموعه عدم اطمینان کران دار معین ایمن نگاه داشت. اولین گام در راستای توسعه نظریه بهینه سازی استوار را سویستر Soyster در سال (۱۹۷۳) برداشته است. رویکرد سویستر برای مواجهه با عدم اطمینان ستون محور در فواصل پیشنهاد شده است؛ این رویکرد بهترین نتایج ممکن را برای هر یک از پارامترهای نادقیق در نظر می گیرد و جواب استواری را ارائه می کند که برای همه داده های نادقیق موجه است؛ با این حال این جواب خیلی محافظه کارانه است و مقدار تابع هدف را خیلی بدتر از تابع هدف با داده های اسمی ارائه می دهد.
بعد از دو دهه، بن تال و نمیروفسکی یا Ben-tal and Nemirovski در سال (۱۹۹۸) و ال قاوی یا El Ghaoui و همکاران در سال (۱۹۹۸) با معرفی مدل هایی برای مسائل خطی نادقیق با عدم اطمینان های بیضی و حال همتای مسائل اسمی در فرم مسائل درجه دوم مخروطی، گامی موثر در این مسیر بر داشتند. بن تال و نمیروفسکی عدم اطمینان سطر محور با ساختار عدم اطمینان بیضی را برای اجتناب از سناریوی بد ترین مورد (که خیلی غیر محتمل است) بررسی کردند و همتای یا Counterpart استواری جدیدی را برای مسئله برنامهریزی خطی توسعه دادند که در آن یک حد بالایی برای تخطی از محدودیت در نظر گرفته می شود. رویکرد پیشنهادی نسبت به رویکرد سویستر کمتر محافظه کارانه، اما مدل حاصله غیر خطی بوده است و در نتیجه برای حل مدل های بهینه سازی گسسته استوار مستقیما کاربردی نیست.
برتسیماس و سیم یا Bertsimas and Sim در سال ۲۰۰۴ رویکرد دیگری برای نمایش عدم اطمینان پارامترها توسعه داده اند. آن ها کران هایی را برای پارامترهای عدم اطمینان در نظر گرفتند که از مقدار اسمی خود متفاوت اند. این رویکرد خانواده ای از همتای استوار را ارائه می کند که ویژگی انعطاف پذیری دارد. رویکرد پیشنهادی این نویسندگان دارای ویژگی های زیر است:
1 – امکان تنظیم سطح حفاظت برای تبادل بین عملکرد و استواری وجود دارد.
2 – امکان محاسبه تضمین احتمال برای ارضای محدودیت ها وجود دارد، به طوری که این ضمانت احتمال به جواب مدل استوار وابسته نیست.
3 – این رویکرد برای مسائل بهینه سازی گسسته قابل استفاده است.
نکته: در بهینه سازی استوار مبتنی بر مجموعه های کران دار، فرض می شود داده های عدم اطمینان در یک مجموعه عدم اطمینان معین توزیع شده اند و هدف انتخاب بهترین جواب از بین جواب هایی است که در برابر عدم اطمینان داده ها مصون یا موجه هستند. توزیع های عدم اطمینان داده ها می تواند یکی از توزیع های پیوسته مانند توزیع یکنواخت، نرمال و گسسته مانند دوجمله ای و پواسن را به خود بگیرد.
مسئله بهینه سازی خطی عدد صحیح زیر را در نظر بگیرید:
متغیرهای x و y به ترتیب متغیرهای پیوسته و عدد صحیح هستند. Mi و Ki زیرمجموعه هایی هستند که به ترتیب متغیرهای پیوسته و گسسته را در بر دارند. ضرایب متغیرهای x و y در معرض عدم اطمینان قرار دارد. ξ پارامترهای نادقیق مستقلی هستند که در بازه [1 ,1-] توزیع می شوند، i-امین محدودیت مسئله اولیه بالا، همان محدودیت (18)، به صورت زیر بازنویسی می شود:
بعد از این گروه بندی، قسمت عدم اطمینان به صورت زیر بازنویسی می شود:
با یک مجموعه عدم اطمینان از پیش تعریف شده U برای متغیرهای تصادفی {ξ={ξi0,ξim,ξik}، به دنبال جوابی هستیم که برای هر ξ در این مجموع موجه باقی بماند تا جواب را در برابر ناموجه بودن ایمن سازیم. یعنی داشته باشیم:
در نهایت با جایگزین کردن محدودیت اولیه iام با محدودیت همتای استوار بالا، همتای استوار مسئله برنامهریزی عدد صحیح مختلط اولیه به دست می آید:
مجموعه های عدم اطمینان
مجموعه عدم اطمینان جعبه ای
مجموعه عدم اطمینان جعبه ای با استفاده از نرم یا Norm بی نهایت بردار داده عدم اطمینان به صورت زیر بیان می شود:
Ψ پارامتر قابل تنظیم است که اندازه مجموعه عدم اطمینان را کنترل می کند.
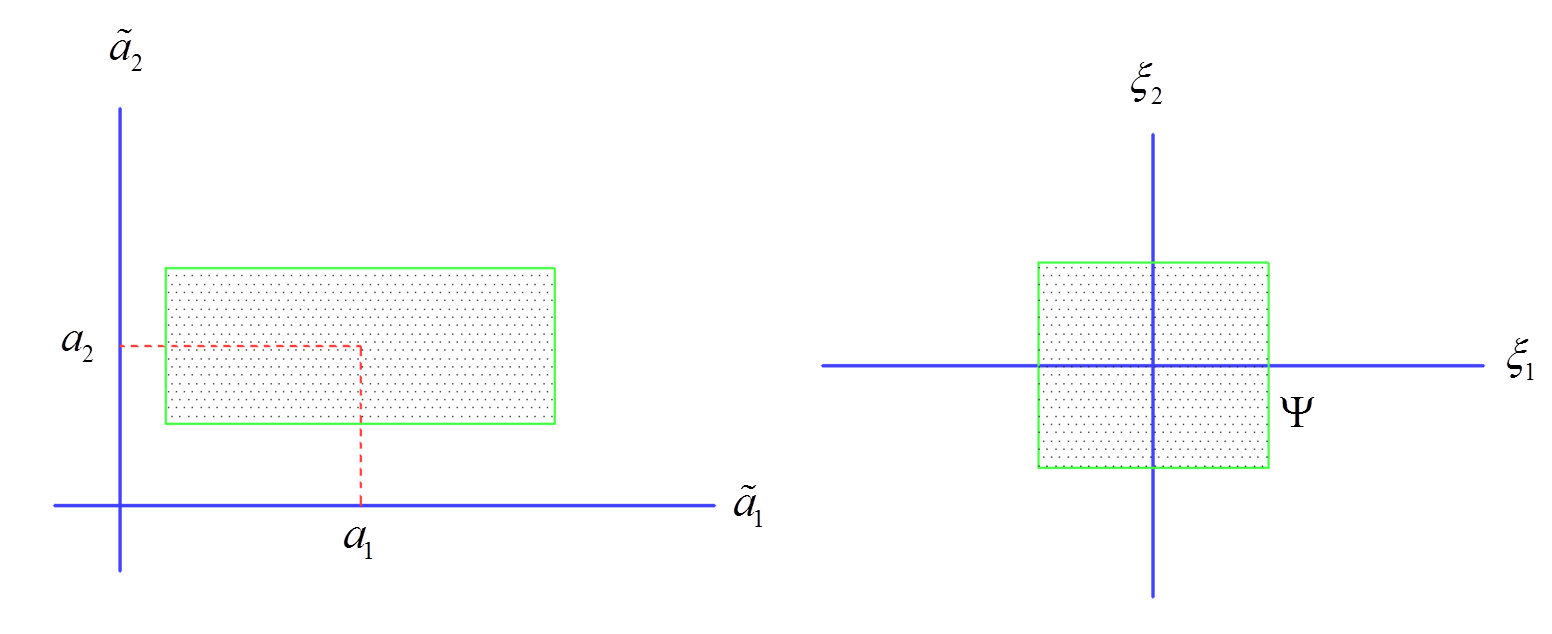
اگر پارامترهای عدم اطمینان در فواصل معین [ ãij ∈ [ aij-âij , aij+âij برای تمامی j که در Ji است، محدود شده باشد، سپس عدم اطمینان به صورت aij+ξ ij× âij=ãij نشان داده می شود، به طوری که ξ ij در بازه [1, 1-] توزیع می شود. وقتی Ψ=1 باشد، مجموعه عدم اطمینان فاصله ای را خواهیم داشت که یک مورد خاص از مجموعه عدم اطمینان جعبه ای است. شکل زیر این نوع مجموعه عدم اطمینان را نشان می دهد.
توجه: برای مطالعه ادامه این درس شامل سایر مجموعه های عدم قطعیت (مانند بیضوی، چند وجهی، و …) ، نحوه مدل سازی همتای استوار مجموعه ها، رویکرد استوار سویستر، رویکرد استوار بن تال و نمیروفسکی، رویکرد استوار برتسیماس و سیم، و حل مثال های متنوع با توضیح کامل، جزوه آموزشی این درس را دانلود کنید.
دانلود بسته طلایی آموزش بهینه سازی استوار و حل تمرین های تشریحی