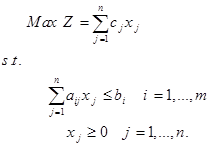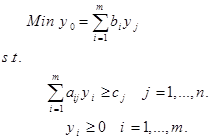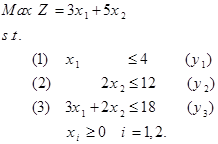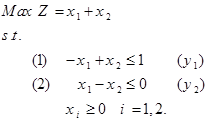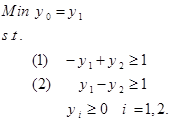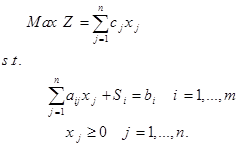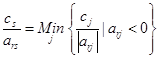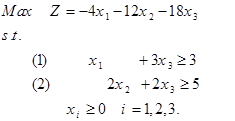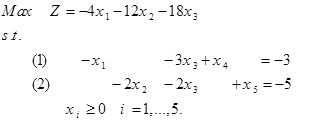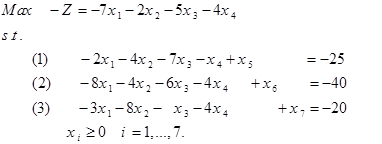برای دانلود خلاصه آموزش نظریه همزادی لطفا ایمیل خود را وارد کنید تا این آموزش برای شما ارسال شود. این آموزش شامل فیلم، جزوه، پادکست و فایل ارایه است.

[/box]

درس 3: نظریه همزادی

تهیه شده توسط گروه بهینه یاب

از جمله مهمترین نتایجی که در دوره‌های نخستین توسعه برنامه‌ریزی خطی بدست آمد، شناخت نظریه دوگانگی یا نظریه همزادی و شاخه‌های مربوط به آن بوده است. در مطالعه‌های اولیه نشان داده شد که هر مسئله برنامه‌ریزی خطی با یک مسئله برنامه‌ریزی خطی دیگر که مسئله همزاد (Dual problem) نامیده می‌شود، ارتباط دارد. برای روشن شدن موضوع نظریه همزادی، مسئله اولیه به شکل استاندارد به صورت زیر را در نظر بگیرید.

اگر y_i را متغیر همزاد هر محدودیت در نظر بگیریم، مسئله همزاد (که از نظریه همزادی گرفته می شود) مدل فوق به صورت زیر بیان می‌شود.

مثال: مدل اولیه زیر را در نظر بگیرید:

مدل همزاد مدل فوق را بنویسید.

حل:

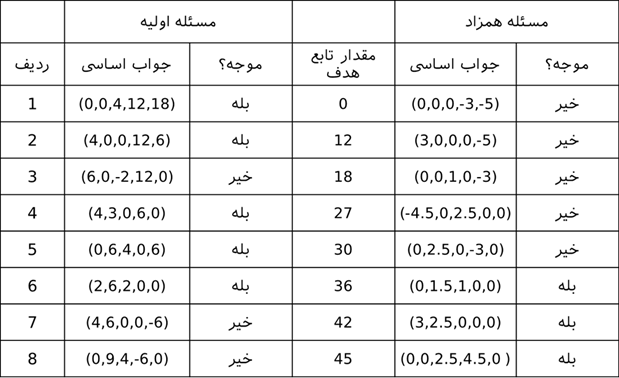
جواب بهینه دو مدل فوق به صورت زیر است:

از جدول فوق مشاهده می‌شود که تنها در یک مورد جواب‌های مسئله اولیه و همزاد موجه هستند و در مابقی حالات یکی از دو مسئله غیر موجه هستند. در جوابی که هر دو مسئله موجه هستند، به جواب بهینه رسیده‌ایم.

تمرین: یک مدل با دو متغیر و دو محدودیت عملکردی بسازید که مدل اولیه جواب نامحدود داشته باشد. از طریق ترسیمی نشان دهید که مسئله همزاد امکان ناپذیر است.

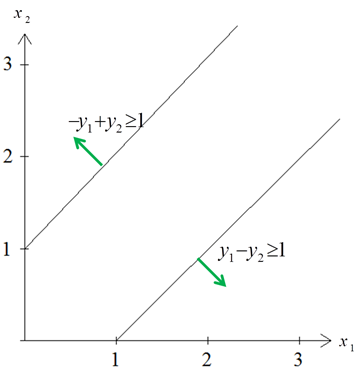
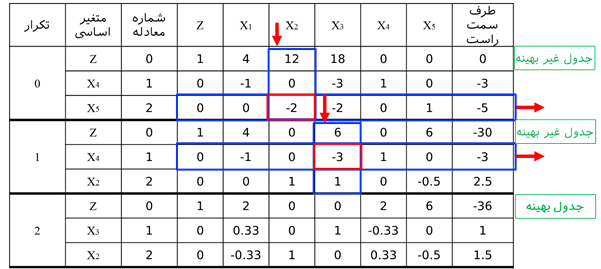
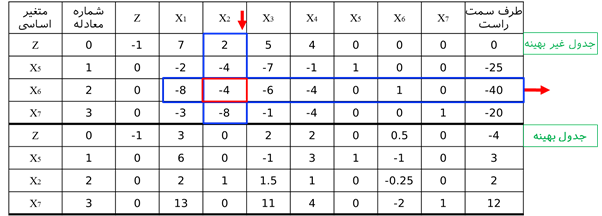
حل:

اگر x₁ = x₂ = c و c به سمت بینهایت میل کند، آنگاه z = 2c و لذا تابع هدف به سمت بینهایت می رود. همزاد مدل فوق به صورت زیر است.

.

حل ترسیمی مدل‌های اولیه و همزاد به صورت زیر است.

.

واضح است که محدوده امکان پذیر مدل همزاد، تهی است.

سیمپلکس همزاد

روش سیمپلکس همزاد برمبنای نظریه همزادی را می‌توان عکس روش سیمپلکس اولیه دانست. روش سیمپلکس اولیه مستقیما با جواب‌های امکان پذیر سروکار دارد و سعی می‌کند تا با ایجاد شرایط بهینگی به طرف جواب بهینه نزدیک شود. در مقابل، روش سیمپلکس همزاد با جواب‌هایی کار می‌کند که شرط بهینگی دارند و با کوشش در جهت موجه کردن آن‌ها، به جواب‌های موجه بهینه نزدیک شود و این روش بر مبنای نظریه همزادی است.

روش سیمپلکس همزاد برمبنای نظریه همزادی در بعضی از شرایط مخصوص فوق العاده مفید واقع می‌شود. گاهی بدست آوردن یک جواب اساسی موجه ابتدایی مستلزم اضافه کردن تعداد زیاد متغیر مصنوعی است. در چنین مواردی، ممکن است شروع کردن از یک جواب بهینه غیرموجه، استفاده از روش سیمپلکس همزاد آسان تر باشد.

برنامه‌ریزی خطی زیر را در نظر بگیرید.

مدل فوق را با اضافه کردن متغیرهای کمبود S_i به فرم استاندارد به صورت زیر در می‌آوریم.

با توجه به مدل فوق، بیان رسمی این روش به صورت زیر می‌شود:

گام 0: در مسئله فوق، c_j ≥ 0 برای تمامی j ها برقرار باشد. اگر برقرار نبود با تغییر متغیر این شرط برقرار شود.

گام 1: اگر به ازای i=1,…,n رابطه b_i ≥ 0 برقرار باشد، توقف کنید زیرا به جواب بهینه حاصل شده است. در صورتی که 0 > b_i باشد، به گام 2 می رویم.

گام 2: سطر لولا ( یعنی متغیر که از پایه حذف می‌شود ) را با استفاده از رابطه زیر انتخاب کنید.

اگر تمامی ضرایب متغیرها در سطر r-ام نا منفی باشد( a_rj ≥ 0, j=1,…,n∀ )، توقف کنید زیرا مسئله امکان ناپذیر است. اگر به ازای مقادیر j=1,…,n داشته باشیم 0 > a_rj برقرار باشد، به گام 3 بروید.

گام 3: ستون s را طبق رابطه زیر تعیین کنید.

در این گام متغیر ورودی به پایه تعیین می‌شود.

گام 4: متغیر S را جایگزین متغیر پایه موجود در سطر r کنید و دوباره فرم استاندارد مدل را با عمل چرخش لولا استاندارد کنید.

گام 5: به گام 1 بروید.

برای روشن شدن الگوریتم فوق، مثال زیر را حل می‌کنیم.

مثال: مدل زیر را به روش سیمپلکس همزاد حل نمایید.

….

برای آغاز حل، می‌بایستی محدودیت ها به صورت ≥ و سپس با اضافه کردن متغیرهای کمبود، فرم محدودیت ها به صورت تساوی درآید. در این صورت مدل به صورت زیر می‌شود.

جواب اساسی مدل فوق به صورت (5-,3-,0,0,0) و Z = 0 است. چون متغیرهای x₄ و x₅ نا مثبت هستند، لذا این جواب اساسی غیر موجه است. اجرای روش سیمپلکس همزاد به صورت زیر می‌شود.

تکرار 0: متغیر را به دلیل این که 5>3 به عنوان متغیر ورودی به پایه انتخاب می‌کنیم. برای انتخاب متغیر خروجی از جواب پایه، از آزمون نسبت استفاده می‌کنیم چون ( 18/2 > 12/2 ) لذا متغیر x₂ به عنوان متغیر خروجی از جواب پایه انتخاب می‌شود. برای خروج x₂ از پایه و ورود x₅ به پایه، سطر معادله 2 را بر 2- تقسیم می‌کنیم.

تکرار 1: شرط توقف را کنترل می‌کنیم. چون 3- بزرگتر از صفر نیست، لذا شرط امکان پذیری جواب برقرار نیست. x₄ به عنوان متغیر خروجی از پایه و با توجه به آزمون نسبت چون ( 6/3 < 4/1 ) است لذا متغیر x₃ وارد پایه می‌شود. برای انجام این تغییرات در جداول سیمپلکس، سطر معادله 1 را بر 3- تقسیم می‌کنیم.

تکرار 2: چون سمت راست معادله نامنفی است لذا شرط امکان پذیری برقرار است و لذا به جواب بهینه رسیدیم و الگوریتم متوقف می‌شود.

تمرین: مسئله زیر را با استفاده از روش سیمپلکس همزاد حل نمایید.

حل: فرم استاندارد مدل فوق به صورت زیر است:

حل مدل فوق به روش سیمپلکس همزاد به صورت زیر می شود.