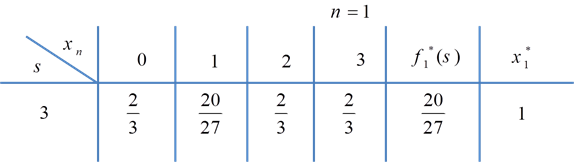برنامه ریزی پویای احتمالی
برای دانلود خلاصه آموزش روش برنامه ریزی پویای احتمالی لطفا ایمیل خود را وارد کنید تا این آموزش برای شما ارسال شود. این آموزش شامل فیلم، جزوه، پادکست و فایل ارایه است.
درس 10: برنامه ریزی پویای احتمالی
تهیه شده توسط گروه بهینه یاب
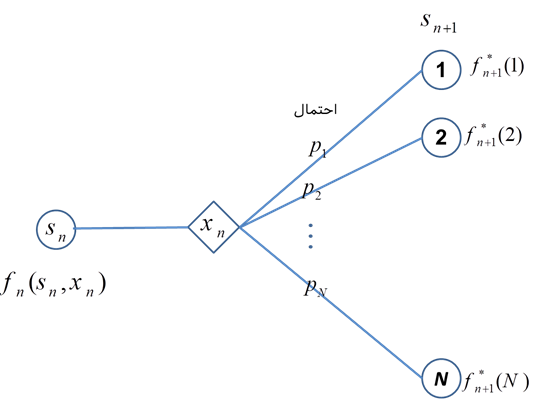
در برنامه ریزی پویای احتمالی، با معلوم بودن حالت و سیاست های تصمیمگیری هر مرحله، حالت قطعی مرحله بعد مشخص نمیشود، بلکه تنها تابع توزیع آن را میتوان تعیین کرد. تصویر کلی برنامه ریزی پویای احتمالی به صورت زیر است.
برای تشریح مسئله، مثال زیر را در نظر بگیرید:
مثال: یک کارشناس آمار مدعی است که روش برنده شدن در یک سلسله مسابقه را پیدا کرده است. دوستانش این ادعا را باور نمیکنند و با او شرط کلانی بسته اند که نمیتواند با سه سکه مسابقه را شروع کرد و در پایان صاحب 5 سکه شود. در هر دور بازی، شرکت کننده میتواند با هر تعداد سکه شرکت کند. اگر ببرد به همان اندازه برنده میشود و اگر ببازد شود همان تعداد سکه ای که شرکت کرده است از دست میدهد. امکان برنده شدن این کارشناس در دور بازی، برآورد شده است. با فرضی که چنین برآوردی صحیح باشد، این متخصص آمار در هر دور بازی از یک بازی سه دوره ای، با چند سکه باید شرکت کند.
حل:
تعداد دوره های بازی (تعداد مرحله) برابر 3 است.
مرحله: دوره های بازی است.
متغیر تصمیمگیری: xn تعداد سکه هایی است که با آن در هر دور بازی شرکت میکند.
حالت: تعداد سکه هایی که این کارشناس آمار در هر مرحله در اختیار دارد.
تابع هدف مسئله: بیشینه کردن احتمال بردن این کارشناس است که به صورت زیر است:
با توجه به موارد فوق، نتایج محاسبات به شرح ذیل است:
مرحله سوم (n=3)
در جدول فوق، نتایج محاسبات برای حالت n=3 آمده است. اگر s=0 باشد، یعنی کارشناس در این مرحله سکه ای برای بازی ندارد و لذا بازنده است. برای s=1 or 2 همین نتیجه گیری درست است. اگر s=3 باشد، یعنی کارشناس 3 سکه برای بازی دارد. اگر با 2 یا بیشتر سکه بازی کند، با احتمال 2/3 برنده میشود و چون در صورت برنده شدن، بیش از 5 سکه دارد، شرط را برده است. اگر s=4 باشد، کارشناس تنها کافی است که با بیش از یک سکه کند که در صورت بردن (با احتمال 2/3 ) حداقل 5 سکه خواهد داشت. اگر وی 5 یا بیشتر از 5 سکه داشته باشد، نیازی به بازی در این مرحله ندارد و قطعا برنده بازی است(با احتمال 1).
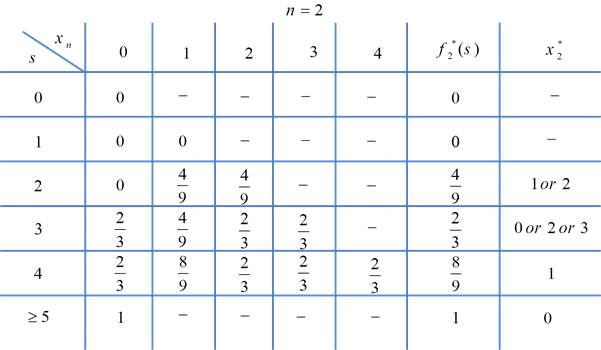
مرحله دوم (n=2)
اکنون n=2 را در نظر بگیرید. فرض کنید x2=0 باشد، اگر s=0، به این معنا است که برای کارشناس سکه ای برای بازی باقی نمانده است و لذا احتمال بردن وی صفر است. اگر s=1 و x2=0 باشد، کارشناس در دور 2 بازی نمیکند و با یک سکه وارد مرحله 3 میشود که احتمال بردن وی با 5 سکه صفر است. برای s=2 همین استدلال برقرار است. اگر s=3 و x2=0 باشد، با بازی نکردن در مرحله 2، کارشناس میتواند با بازی کردن با بیش از 2 سکه با احتمال 2/3 برنده شود.
اکنون فرض کنید x2=1 شود. s=0 به این معنا است که کارشناس سکه ای برای بازی ندارد لذا نمیتواند اصلا بازی کند و لذا برای این حالت – استفاده شده است. فرض کنید s=1 و x2=1 باشد. در این حالت کارشناس یک سکه دارد و با یک سکه در این مرحله شرط بندی میکند. در این صورت با احتمال 1/3 بازنده میشود و در مرحله 3 سکه ای ندارد و با احتمال 2/3 برنده میشود و 2 سکه خواهد داشت که در هر صورت احتمال بردن شرط بندی را ندارد. بیان ریاضی عبارت قبل به صورت زیر است.
فرض کنید s=2 و x2=1 باشد، مقدار احتمال بردن بازی به صورت زیر محاسبه میشود:
فرض کنید s=3 و x2=1 باشد، مقدار احتمال بردن بازی به صورت زیر محاسبه میشود:
فرض کنید s=4 و x2=1 باشد، مقدار احتمال بردن بازی به صورت زیر محاسبه میشود:
سایر مقادیر به طریق مشابه قابل محاسبه است.
مرحله اول (n=1)
جزییات محاسبات برای n=1 جدول فوق در زیر آمده است.
فرض کنید s=3 و x1=0 باشد، مقدار احتمال بردن بازی به صورت زیر محاسبه میشود.
فرض کنید s=3 و x1=1 باشد، مقدار احتمال بردن بازی به صورت زیر محاسبه میشود.
سایر مقادیر به طرق مشابه محاسبه میشود.
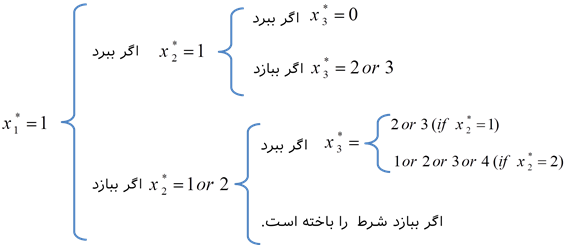
نتایج سه جدول اخیر میتوان سیاست احتمالی بهینه را به صورت زیر خلاصه کرد:
طبق سیاست فوق، این کارشناس با احتمال 20/27 شرط را میبرد.