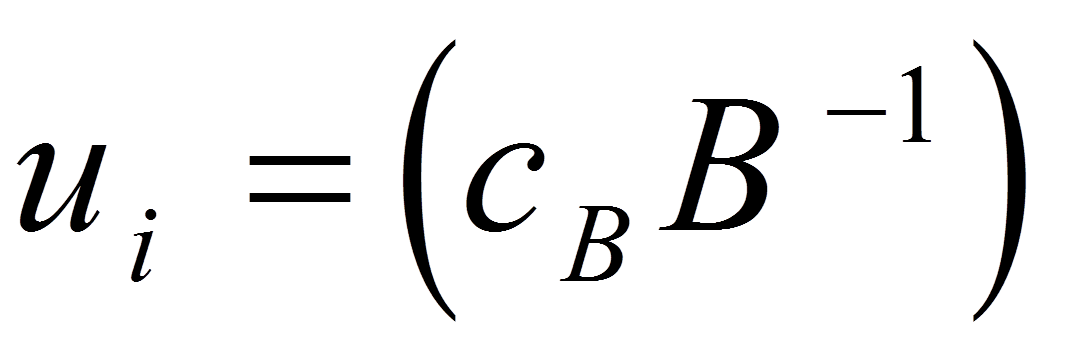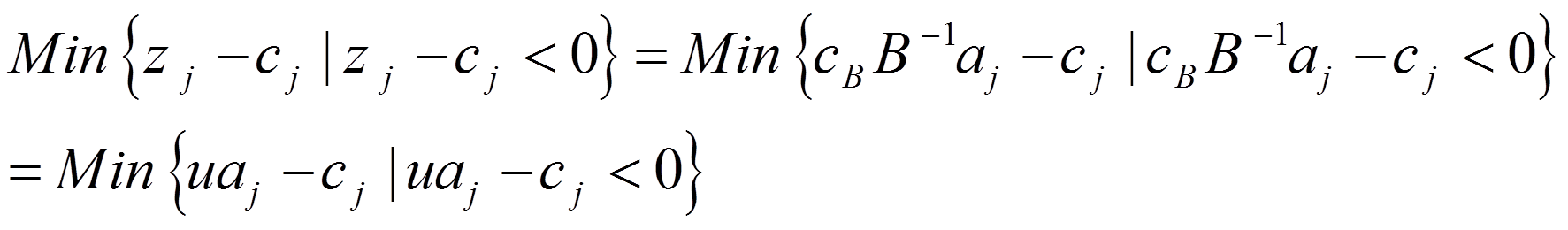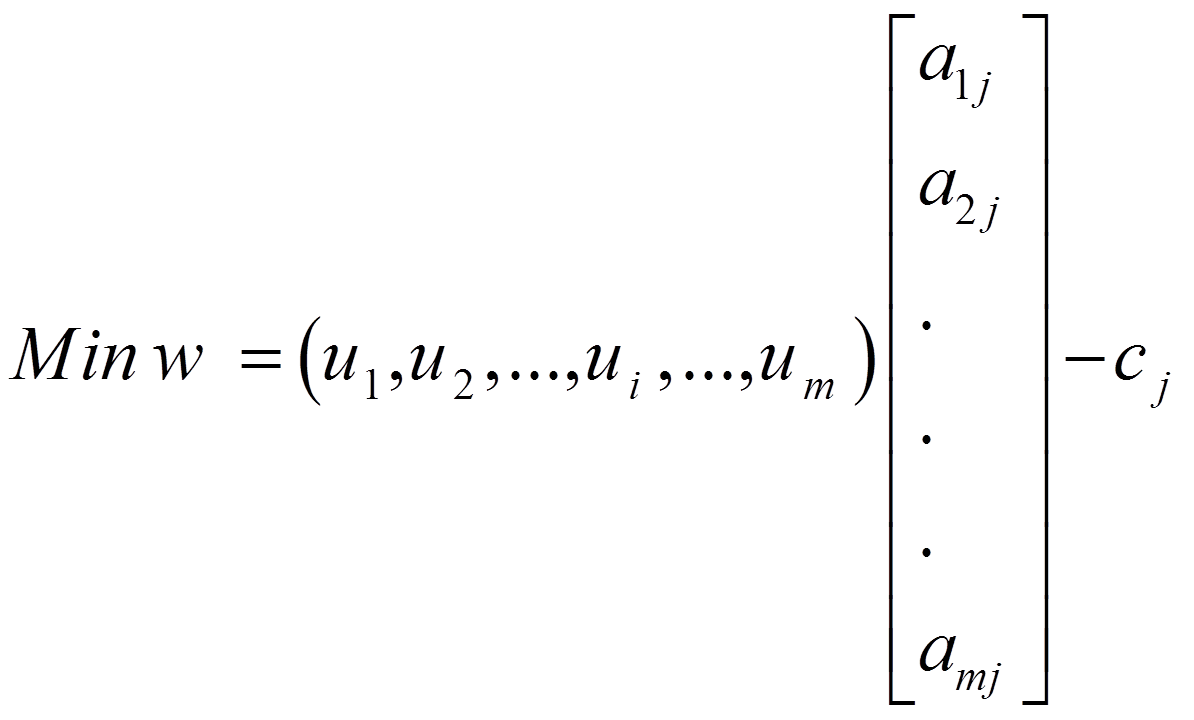درس 35: آموزش الگوریتم تولید ستون

تهیه شده توسط گروه بهینه یاب

آ

مقدمه

روش تولید ستون یا column generation یکی از روش های موثر در حل مسائل برنامه ریزی خطی با ابعاد بزرگ به خصوص در مواردی است که تعداد متغیرها بسیار بیشتر از تعداد محدودیت ها است و به عبارتی ماتریس ضرایب مسئله دارای ستون های زیادی است. این روش را در دهه شصت میلادی گیلمور و گموری طراحی کردند. در چنین مسائلی در حالت ازادسازی خطی تعدد متغیرهای غیر پایه که صفر هستند، بسیار زیاد است در حالی که فقط تعداد محدودی از متغیرها در پایه قراردارند و دارای مقادیر غیر صفر می باشند. برای این منظور در این روش مسئله اولیه به دو زیر مسئله تفکیک می شود، زیر مسئله اصلی و زیر مسئله فرعی. زیر مسئله اصلی در حقیقت زیر مسئله کوچکی از مسئله اولیه است که با فقط زیر مجموعه ای از متغیرها تشکیل می شود. حل زیر مسئله اصلی که یک مدل برنامه ریزی خطی است، باعث شناسایی مقادیر متغیرهای همزاد می شود. از مقادیر متغیرهای همزاد حاصل از زیر مسئله اصلی استفاده می شود تا زیر مسئله فرعی تشکیل شود و با حل ان، متغیر ورودی و ستون مربوط به آن شناسایی و دوباره به زیر مسئله اصلی وارد می شود و این فرایند ارتباط بین پاسخ های مسئله اصلی و فرعی تا انجا ادامه می یابد که شرط توقف الگوریتم برآورده شود. جزییات به کارگیری این روش در ادامه آمده است.

شرح الگوریتم تولید ستون برای حل یک مسئله برنامه ریزی خطی

یک مسئله برنامه ریزی خطی را به صورت زیر در نظر بگیرید:

اگر ماتریس A در این مدل که یک ماتریس m*n (m سطر و n ستون) فرض می شود بسیار بزرگ باشد، به معنی آن است که دارای تعداد قبل توجهی ستون است که در هر پاسخ پایه مسئله فقط از m ستون آن برای تشکیل وارون ماتریس پایه و پاسخ های پایه استفاده شده و سایر ستون ها آن یعنی n-m ستون وابسته به متغیرهای غیرپایه ای صفر است که در تکرار فعلی استفاده نشده و در تکرار بعد هم قرار است فقط یکی از ستون های ان استفاده شود که وابسته به متغیر ورودی است. افزون بر این مسئله در بسیاری از مسائل واقعی اصولا تشکیل ماتریس A از ابتدا در مسئله اصلی نیازمند صرف زمان و وقت بسیار است و در مواردی اصولا تعیین تمام ستون ها تشکیل دهنده آن امکان پذیر نیست.

در روش تولید ستون می خواهیم بدون این که نیاز به شناسایی تمام ستون های ماتریس A باشد، ابتدا با حداقل تعداد مورد نیاز یعنی m ستون از ماتریس A شروع کنیم و زیر مسئله برنامه ریزی خطی آن را موسوم به زیر مسئله اصلی حل کنیم و سپس با وجود  این که تمام ستون های ماتریس A را نمی دانیم، با تشکیل زیر مسئله فرعی و حل آن یکی از ستون های آن را به عنوان ستون متغیر ورودی به پایه تولید کرده و سپس آن را وارد زیر مسئله اصلی کنیم. حل جزییات زیرمسائل اصلی و فرعی را شرح می دهیم:

زیر مسئله اصلی محدود شده RMP

این زیر مسئله در ابتدا فقط شامل بخش کوچکی از مسئله اولیه، یعنی یک زیرماتریس m*m از ماتریس A است. تولید این ستون ها با توجه به مسئله اولیه انجام می شود. سپس در هر تکرار قرار است یک ستون جدید که از حل زیر مسئله فرعی به دست می اید، به آن اضافه شود. زیر مسئله اصلی RMP یک زیر مسئله از نوع LP است و می توان پاسخ را از روش سیمپلکس به دست اورد. البته با حل این مسئله، پاسخ متغیرهای دوگان آن نظیر u به دست خواهند امد که برای این روش مهم است زیرا این متغیرهای همزاد در زیر مسئله فرعی استفاده می شوند.

زیرمسئله فرعی قیمت گذاری

در این زیر مسئله قرار است بدون این که تمام بردارهای ستونی مربوط به ماتریس A را بدانیم، بردار ستونی مربوط به متغیر ورودی به پایه را برای زیر مسئله محدود شده RMP به دست آوریم. می دانیم که در یک مسئله برنامه ریزی خطی با تابع هدف Max متغیر ورودی به پایه متغیری است که دارای شرط بهینگی به صورت زیر باشد:

از طرف دیگر داریم:

که در آن u متغیرهای دوگان حاصل از پاسخ زیر مسئله اصلی RMP است. از نظریه برنامه ریزی خطی می دانیم (z_j-c_j) را هزینه کاهش یافته یا Reduced cost می نامند زیرا تفاوت z_j یعنی قیمت تمام شده برای تولید یک واحد محصول j وc_j سود حاصل از هر واحد محصول j است. در یک مسئله حداکثر سازی، متغیر ورودی متغیری است که در آن تفاوت سود تولید هر واحد آن نسبت به قیمت تمام شده هر واحد آن بیشتر باشد، به عبارتی c_j-z_j بزرگتری داشته باشد. برای این که این مقدار بزرگتر باشد چون معمولا امکان افزایش سود وجود ندارد، باید هزینه های تولید محصول و یا به عبارتی همان قیمت تمام شده آن کاست و زیر مسئله فرعی را که براساس تولید می شود، زیر مسئله قیمت گذاری یا pricing subproblemمی نامند. حال از نظریه دوگانگی در برنامه ریزی خطی می دانیم که مقدار متغیر دوگان وابسته به محدودیت i ام مسئله اولیه برابرست با:

پس زمانی که می خواهیم بردار a_j را از بین بردارهای ستون ماتریس A بدست آوریم، به نحوی که مربوط به متغیر ورودی به پایه مسئله اصلی باشد، کافی است داشته باشیم.

چون بردار سطری مقادیر متغیرهای همزاد یعنی u=(u₁,u₂,…,u_i,…,u_m) را می دانیم، پس می توان تعیین بردار a_j را با حل مسئله زیر تعیین کرد.

در مسئله بالا عناصر بردار a_j باید در بین خودشان شرایط موجود در مسئله اولیه را رعایت کنند که محدودیت های آن معمولا به صورت خطی است که فضای موجه آن را S در نظر می گیریم.

همان طور که مشخص است، تابع هدف زیر مسئله بالا یا همان z_j-c_j مربوط به هر متغیر در جدول سیمپلکس است که در آن مقادیر متغیرهای همزاد از حل زیر مسئله اصلی محدود شده RMP تولید می شود. با حل زیر مسئله فرعی بردار a_j به دست می اید. اگر پاسخ تابع هدف زیر مسئله فرعی در یک مسئله با تابع هدف حداکثر سازی مقدار مثبتی شد بدین معنی است که شرط بهینگی برآورد شده است و به نقطه پایانی و پاسخ بهینه رسیده ایم. ولی در صورتی که مقدار تابع هدف منفی شد، بردار ستون a_j باید به زیر مسئله اصلی محدود شده RMP اضافه شود و الگوریتم در تکرار بعدی ادامه می یابد.

مسئله کاهش ضایعات برش یا cutting stock problem

برای مشاهده ادامه این درس شامل ارایه حل مسئله کاهش ضایعات برش، و پیاده سازی این روش، بسته های آموزشی این درس را به شرح ذیل تهیه نمایید.