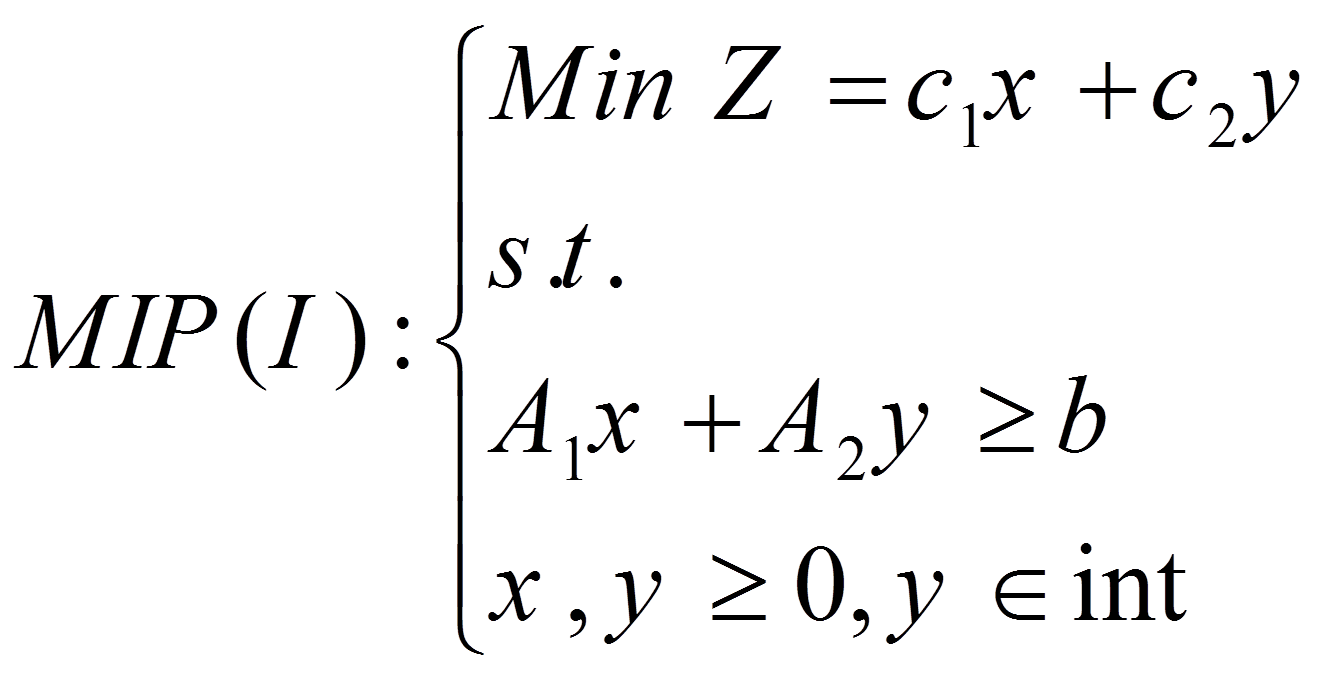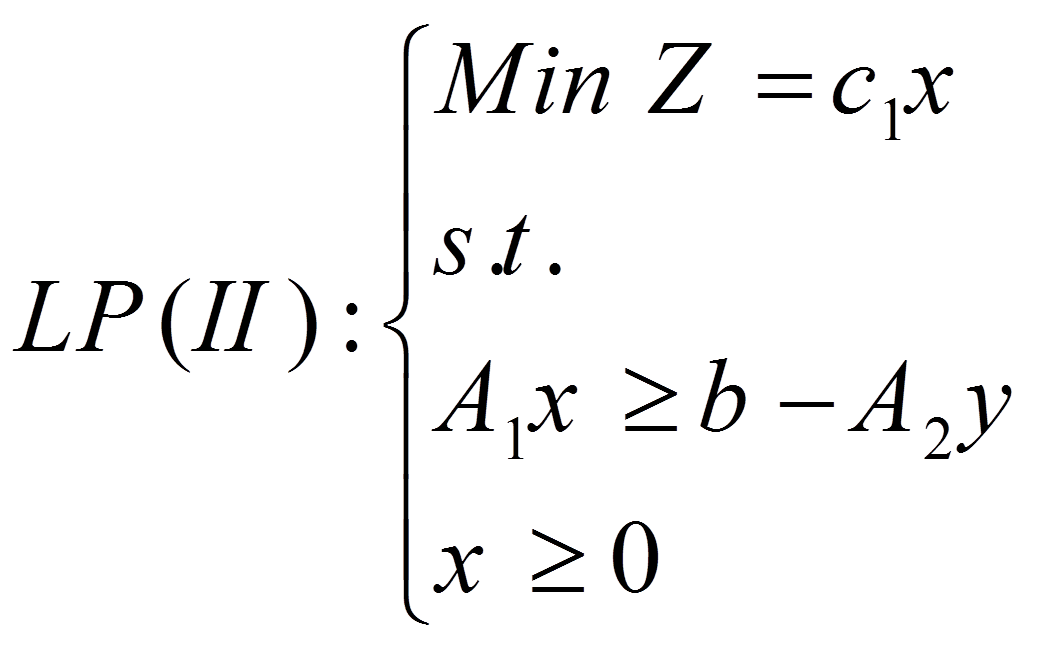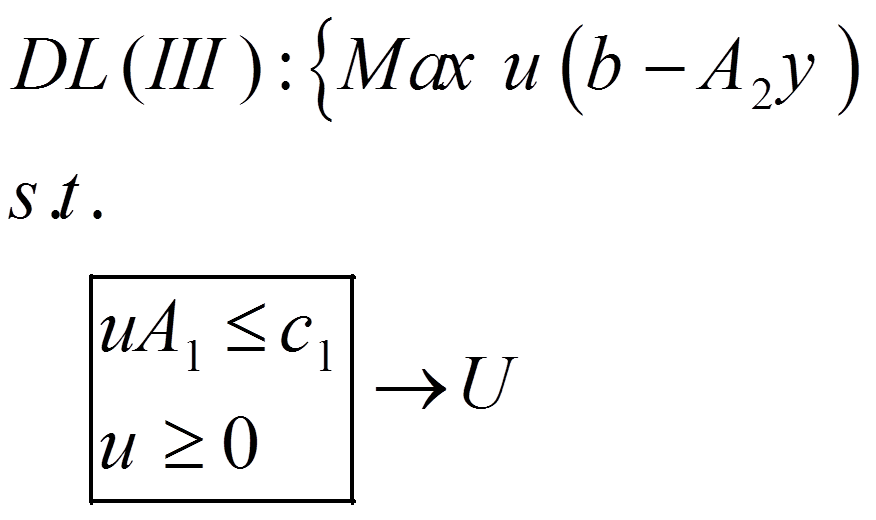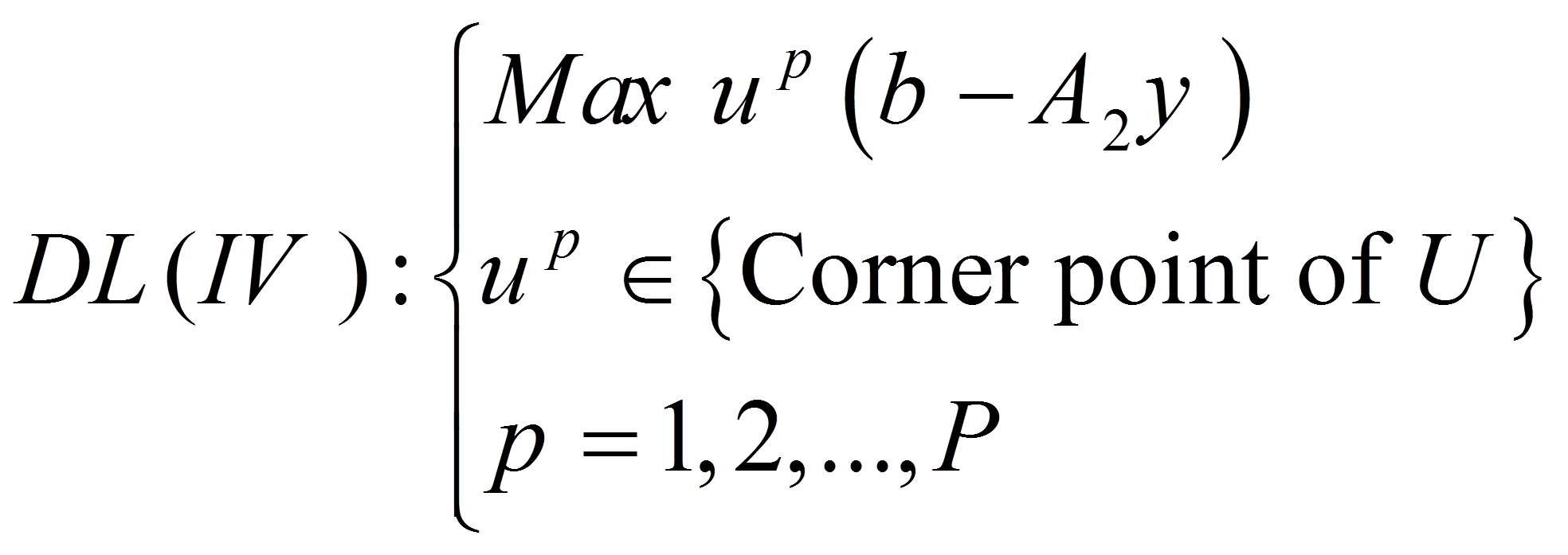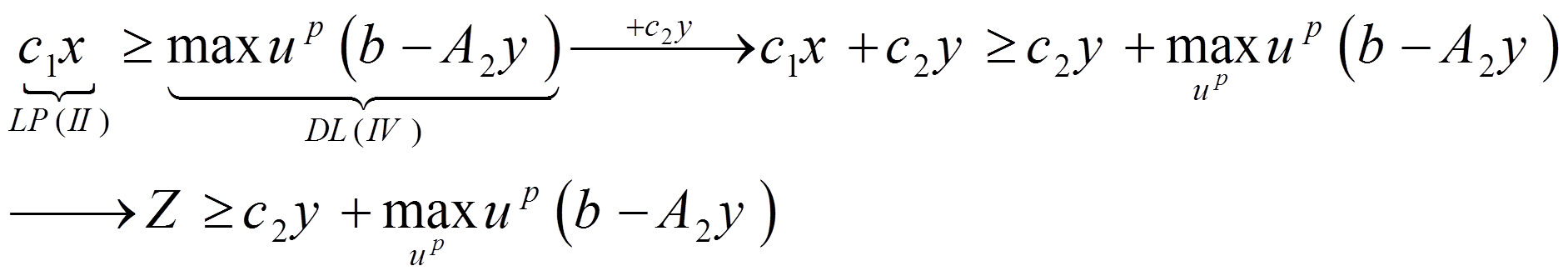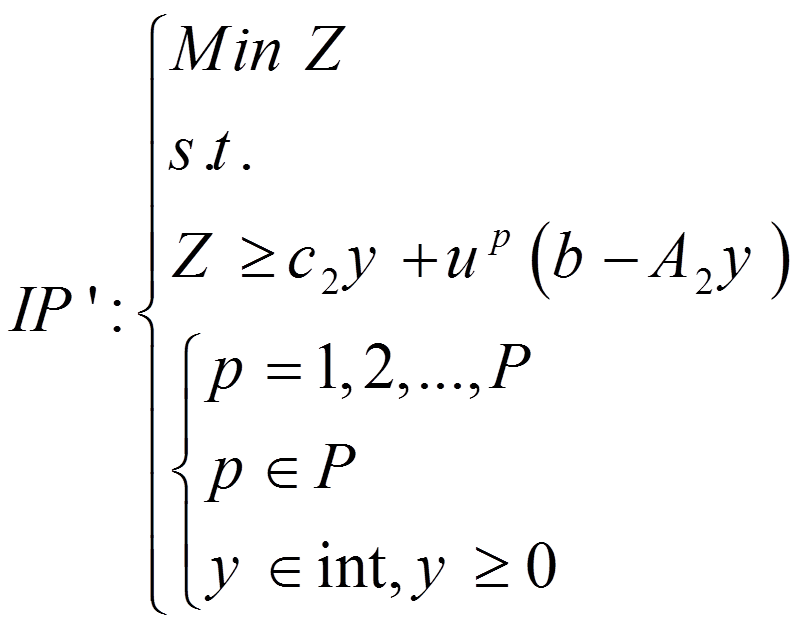درس 34: آموزش الگوریتم تجزیه بندرز

تهیه شده توسط گروه بهینه یاب

آ

مقدمه

در این درس به دنبال پیاده سازی الگوریتم تجزیه بندرز در برنامه ویژوال بیسیک هستیم. در ابتدا مروری بر الگوریتم تجزیه بندرز می کنیم. سپس یک مدل بهینه سازی را با استفاده از این الگوریتم حل می کنیم و در نهایت این مدل را با استفاده از زبان ویژوال بیسیک با الگوریتم بندرز برنامه نویسی می کنیم.

شرح کلی روش بندرز

این روش را ریاضی دان آلمانی، ژاکوب بندرز، برای حل مسائل برنامه ریزی مختلط MIP طراحی کرده است. در ابتدا مسئله MIP به دو زیر مسئله تقسیم می شود و سپس تبادل پاسخ های بین این دو زیر مسئله تا زمان رسیدن به پاسخ نهایی مسئله اصلی صورت می گیرد. فرض کنید مسئله MIP زیر داده شده است که در آن متغیرهای x متغیرهای پیوسته غیرمنفی و متغیرهای y متغیرهای عدد صحیح غیرمنفی هستند.

حال فرض کنیم متغیرهای عدد صحیح y در یک مقدار صحیح غیر منفی ثابت شوند، در این صورت عبارت مربوط به y در تابع هدف زیر به یک مقدار ثابت تبدیل می شود و از تابع هدف حذف شدنی است و به مدل خطی زیر می رسیم:

چون مدل II خطی است، پس برای آن همزاد قابل تعریف است که اگر متغیرهای دوگان آن را u فرض کنیم، مسئله همزاد متناظر با آن به صورت زیر در می آید:

در مسئله DL(III) اگر فضای پاسخ را U در نظر بگیریم:

• U مستقل از متغیر y است.
• اگر U تهی باشد، مسئله DL(III) دارای پاسخ موجه نیست. آنگاه طبق نظریه همزادی مسئله LP(II) یا ناموجه است و یا بیکران. ولی اگر مسئله LP(II) بیکران باشد، به این معنی است که مسئله اصلی MIP(I) بیکران است اما چون در مسائل عملی و واقعی MIP(I) بیکران نیست، پس فرض زیر را در مورد این مسئله خواهیم داشت:

فرض 1: فضای پاسخ U تهی نیست و مسئله DL(III) موجه است.

• چون مسئله DL(III) مستقل از y است و طبق فرض (1) غیرتهی است، پس حداکثر مقدار تابع هدف یعنی maxu(b-A₂y) یا روی نقاط گوشه U اتفاق می افتد و یا در امتداد یکی از شعاع های حدی یا extreme rays فضای U افزایش نامحدود می یابند. برای جلوگیری از بیکران شدن پاسخ این مسئله فرض زیر را اضافه می کنیم.

فرض 2: فضای پاسخ U محدود است و مسئله DL(III) دارای پاسخ بهینه محدود است و بیکران نیست، پس دارای شعاع حدی نیست.

البته حتی اگر در مسئله DL(III) فضای پاسخ بیکران بود نیز روش بندرز استفاده می شود زیرا برای تحقق فرض (2) می توان محدودیتی بدیهی نظیر مجموع تمام متغیرها کوچکتر یا مساوی یک مقدار بزرگ به صورت به مسئله اضافه شود.

با توجه به فرضیات (1)  و (2) می توان گفت پاسخ بهینه محدود DL(III) روی نقاط گوشه U خواهد بود و این مسئله را می توان به شکل زیر نیز نوشت:

کار ما بدین صورت خواهد بود که تمام نقاط گوشه مسئله DL(IV) را شمارش کرده، از بین آن ها بهترین را انتخاب کنیم، اما شمارش تمام نقاط گوشه بسیار وقت گیر است و تعداد محدودیت های جبری برای تولید آن می توان بی شمار شود. پس باید تمهیدی اندیشید تا با کمترین بررسی در نقاط گوشه آن به پاسخ بهینه رسید.

از نظریه دوگانگی در برنامه ریزی خطی می دانیم که طبق خاصیت ضعیف دوگانگی داریم:

در روابط بالا، c₂y را که بیشتر کم کرده، به دو طرف نامساوی اضافه کردیم و در نهایت نتیجه می گیریم مقدار تابع هدف مسئله اصلی MIP(I) دارای یک حد پایینی است که به ازای شمارش نقاط گوشه فضای U  به دست می آید. پس می توان مسئله MIP(I) را به صورت زیر نوشت:

مسئله IP’ یک مسئله عدد صحیح خالص است. به عبارت دیگر به جای حل مسئله MIP(I) که یک مسئله عدد صحیح مخلوط بود، یک مسئله را که عدد صحیح خالص است، حل می کنیم. البته در عمل به جای شمارش کامل تمام نقاط گوشه مسئله DL(IV) که هر کدام یک نا معادله را به مسئله IP’ اضافه می کنند، امیدواریم با تنها یک تعداد از این نقاط گوشه بتوانیم پاسخ بهینه مسئله اصلی MIP(I) را تولید کنیم.

برای مشاهده ادامه این درس شامل ارایه الگوریتم تجزیه بندرز، حل یک مثال و پیاده سازی این روش، بسته های آموزشی این درس را به شرح ذیل تهیه نمایید.