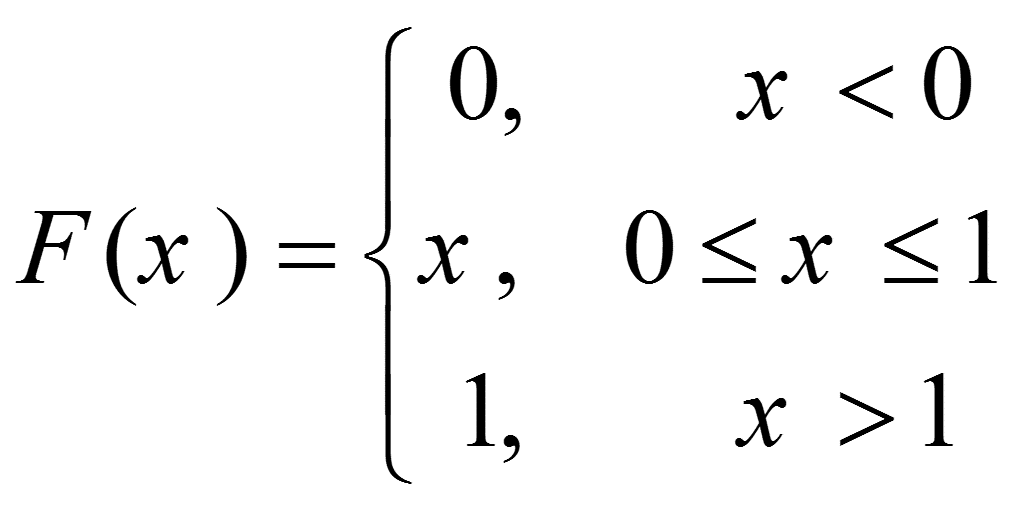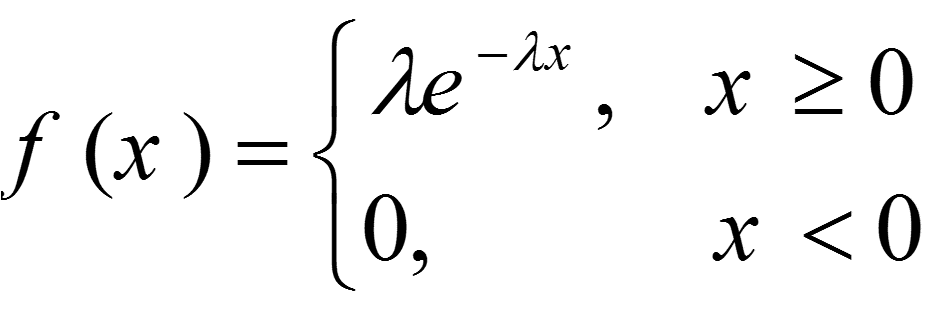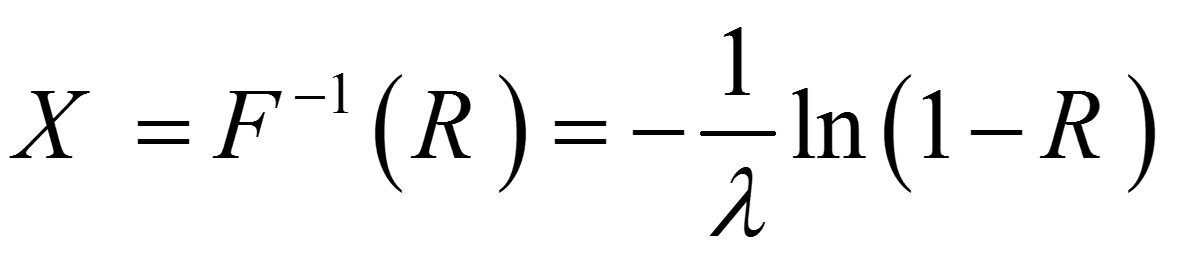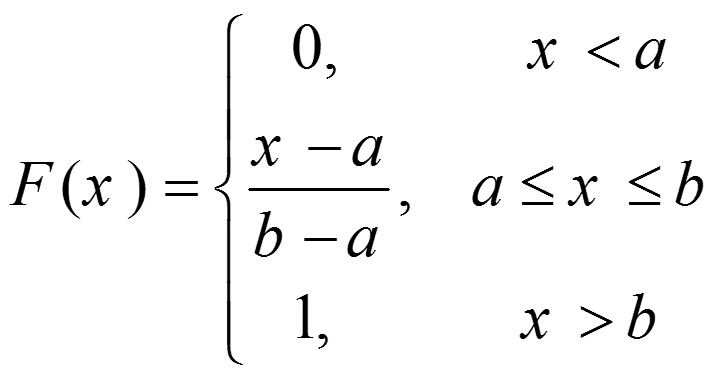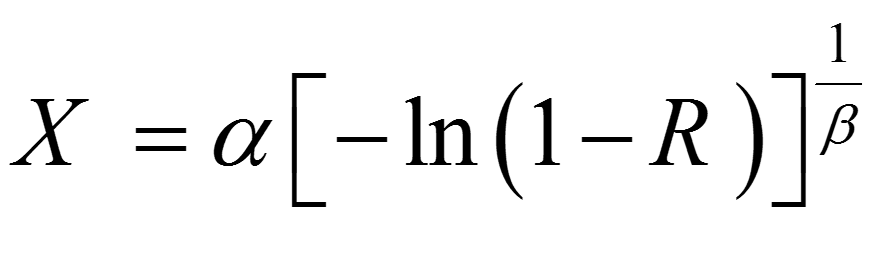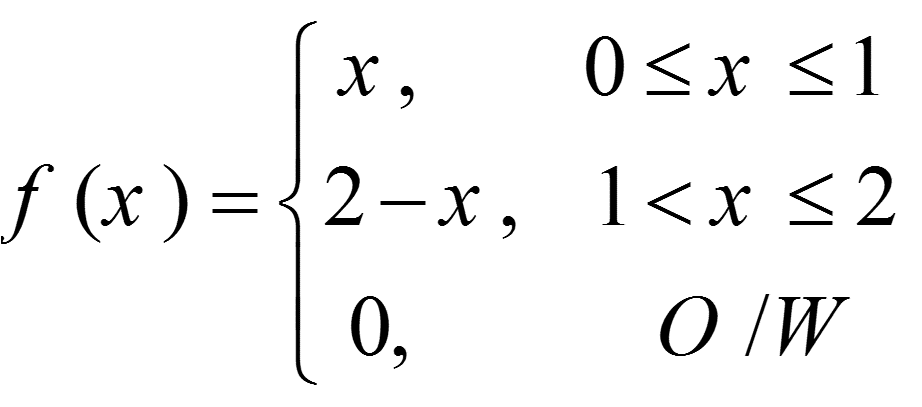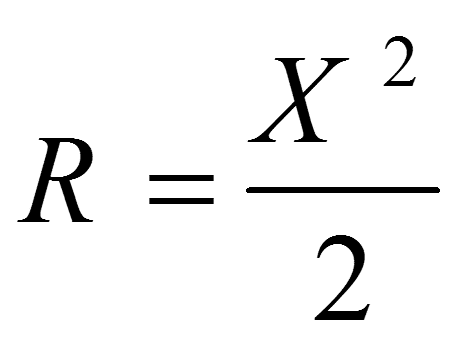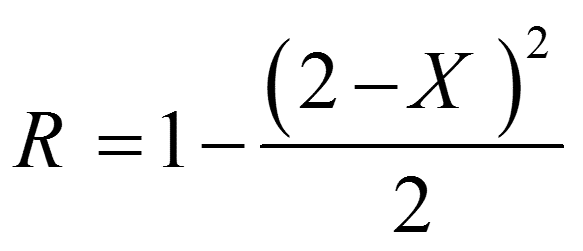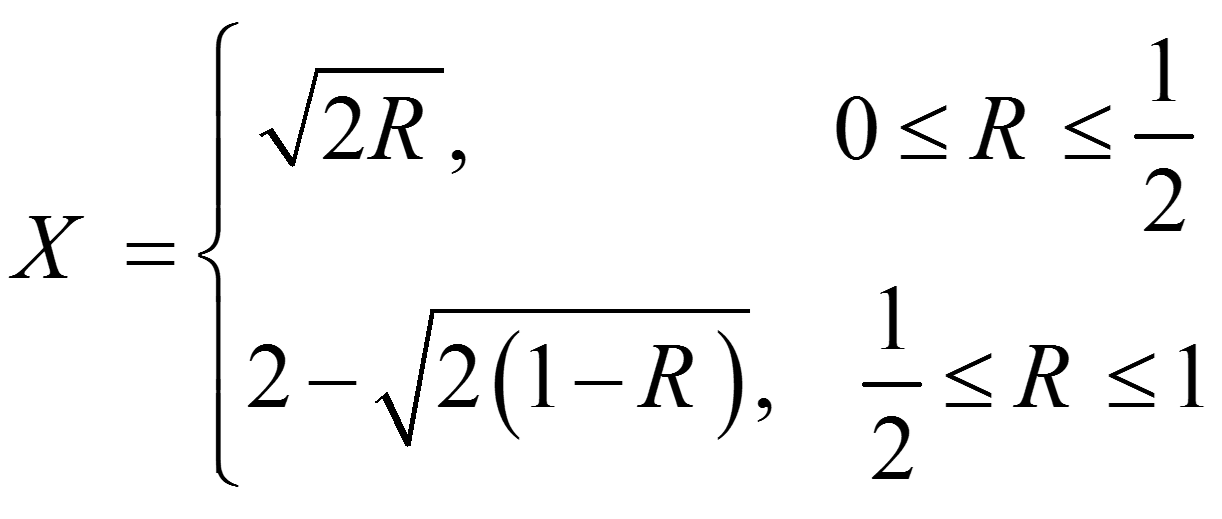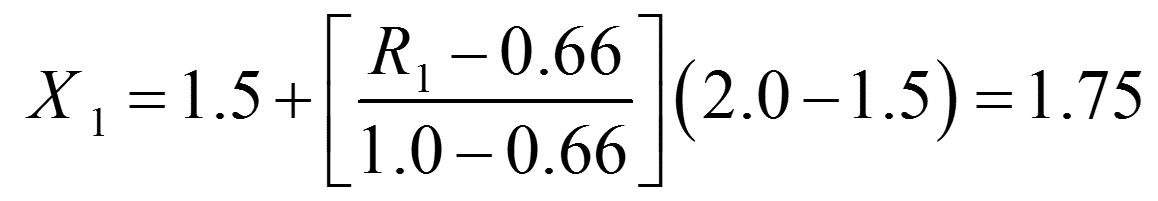برای دانلود خلاصه آموزش تولید متغیر تصادفی لطفا ایمیل خود را وارد کنید تا این آموزش برای شما ارسال شود.
دانلود جزوه آموزش روش های تولید متغیر تصادفی و حل تمرین های کاربردی
درس 26: تولید متغیر تصادفی
تهیه شده توسط گروه بهینه یاب
آ
مقدمه
این درس به شیوههایی برای نمونه گیری از انواع توزیعهای پیوسته و گسستهای میپردازد که به طور گستردهای مورد استفاده قرار می گیرد. بحث ها و مثالهای پیشین از سیستمهای صف، بر فایده توزیعهای آماری برای مدل سازی فعالیتهای دلالت داشته که عموما غیرقابل پیش بینی یا ناقطعی است. مثلا، مدتهای بین دو ورود و مدتهای خدمت دهی در صف ها و تقاضا برای یک محصول، دست کم تا حد معینی، اغلب ماهیتی غیرقابل پیش بینی دارند. معمولا، چنین متغیرهایی به صورت متغیرهایی تصادفی با توزیع آماری مشخص مدلسازی می شود و برای براورد پارامترهای توزیع فرضی و آزموندن اعتبار مدل آماری مفروض، شیوههای استاندارد آماری وجود دارد.
در این درس فرض می کنیم که توزیعی به طور کامل مشخص شده است و ما در جستجوی راههای به منظور تولید نمونههایی از این توزیع برای استفاده به عنوان ورودی به مدل شبیه سازی هستیم.
در همه روشهای این فصل فرض می کنیم که یک منبع اعداد تصادفی یکنواخت (0,1) ، R1,R2,…، در دسترس است که برای هر یک از که دارای تابع توزیع
و تابع توزیع تجمعی
است. در این درس، R1,R2,R3,… یا R معرف اعداد تصادفی با توزیع یکنواخت بین صفر و یک است.
روش تبدیل معکوس
در ادامه به تابع توزیع هایی می پردازیم که امکان یافتن تابع معکوس آن ها به سادگی مسیر است.
تابع توزیع نمایی
توزیع نمایی دارای تابع چگالی زیر است:
و تابع توزیع تجمعی به صورت زیر است:
به دلیل این که امکان محاسبه تابع معکوس تابع توزیع تجمعی به صورت صریح وجود دارد، روش گام به گام روش تبدیل معکوس برای توزیع نمایی به صورت زیر می شود:
گام 1: تابع توزیع تجمعی نمایی متغیر تصادفی X را به صورت زیر در نظر بگیرید:
گام 2: فرض کنید در دامنه X برقرار است.
گام 3: معادله (R=F(X را حل کنید تا X برحسب R بدست آید:
گام 4: اعداد تصادفی یکنواخت R1، R2، R3 و … را تولید و مقادیر موردنظر را طبق رابطه زیر
محاسبه کنید.
تابع توزیع یکنواخت
یک متغیر تصادفی مانند X را در نظر بگیرید که در فاصله [a,b] به طور یکنواخت توزیع شده است. تابع تولید متغیر تصادفی X عبارت است از:
تابع چگالی X به صورت زیر ارایه میشود.
برای تولید اعداد تصادفی با توزیع یکنواخت گامهای زیر انجام میشود:
گام 1: تابع توزیع تجمعی یکنواخت به صورت زیر است:
گام 2: معادله زیر را در نظر بگیرید:
گام 3: حل X بر حسب R به رابطه زیر میآنجامد:
توزیع ویبول
در توزیع ویبول، هر گاه پارامتر موقعیت یا v برابر با صفر باشد، آنگاه تابع توزیع احتمال به صورت زیر میتوان نوشت:
در تابع فوق، α>0 و β>0 که به ترتیب پارامترهای مقیاس و شکل هستند. به منظور تولید هر مقدار تصادفی از توزیع ویبول، گامهای 1 تا 3 را به صورت زیر انجام می دهیم:
گام 1: تابع توزیع تجمعی به صورت زیر تعریف میشود:
گام 2: برای متغیر تصادفی R به صورت زیر داریم.
گام 3: حل X بر حسب R به نتیجه زیر میآنجامد:
توزیع مثلثی
متغیر تصادفی مانند X را در نظر بگیرید که دارای تابع توزیع زیر است:
تابع توزیع تجمعی این توزیع به صورت زیر میشود.
به ازای این که X بین صفر و یک باشد داریم
و به ازای این که X بین یک و دو باشد داریم:
با استفاده از رابطه بالا می توان برای R دو حالت زیر را متصور بود:
بنابراین میتوان تولید متغیر تصادفی براساس تابع توزیع مثلثی را به صورت زیر بیان کرد:
توزیعهای تجربی پیوسته
اگر مدل ساز نتواند از یافتن توزیعی نظری به منظور ارایه مدل مناسبی برای دادههای ورود باشد. ممکن است استفاده از توزیع تجربی دادهها لازم شود.
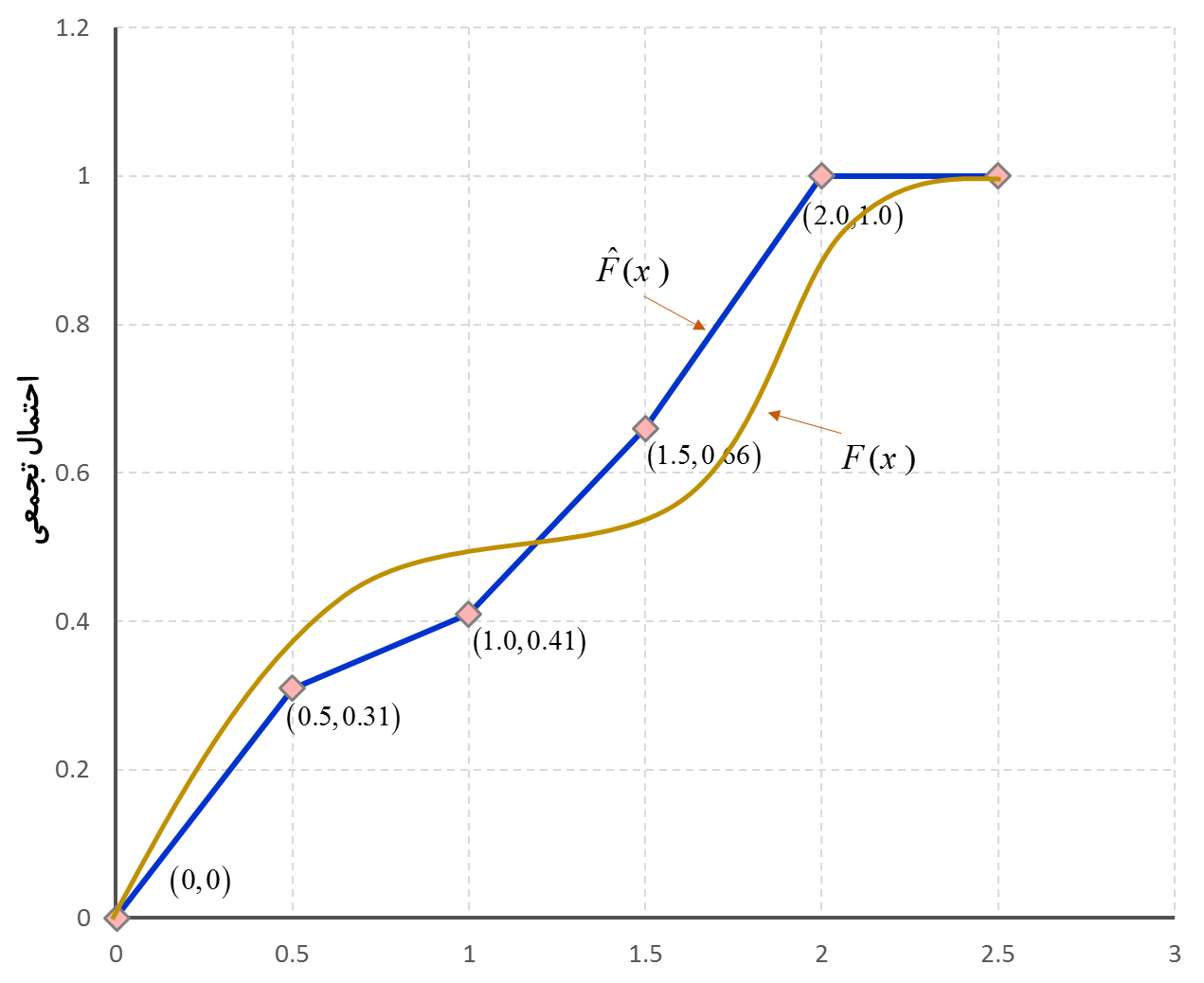
مثال: تصور کنید 100 مورد مدت تعمیر نوعی ابزار شکسته گردآوری شده و دادهها بر حسب تعداد مشاهده در فواصل مختلف، در جدول زیر خلاصه شده است.
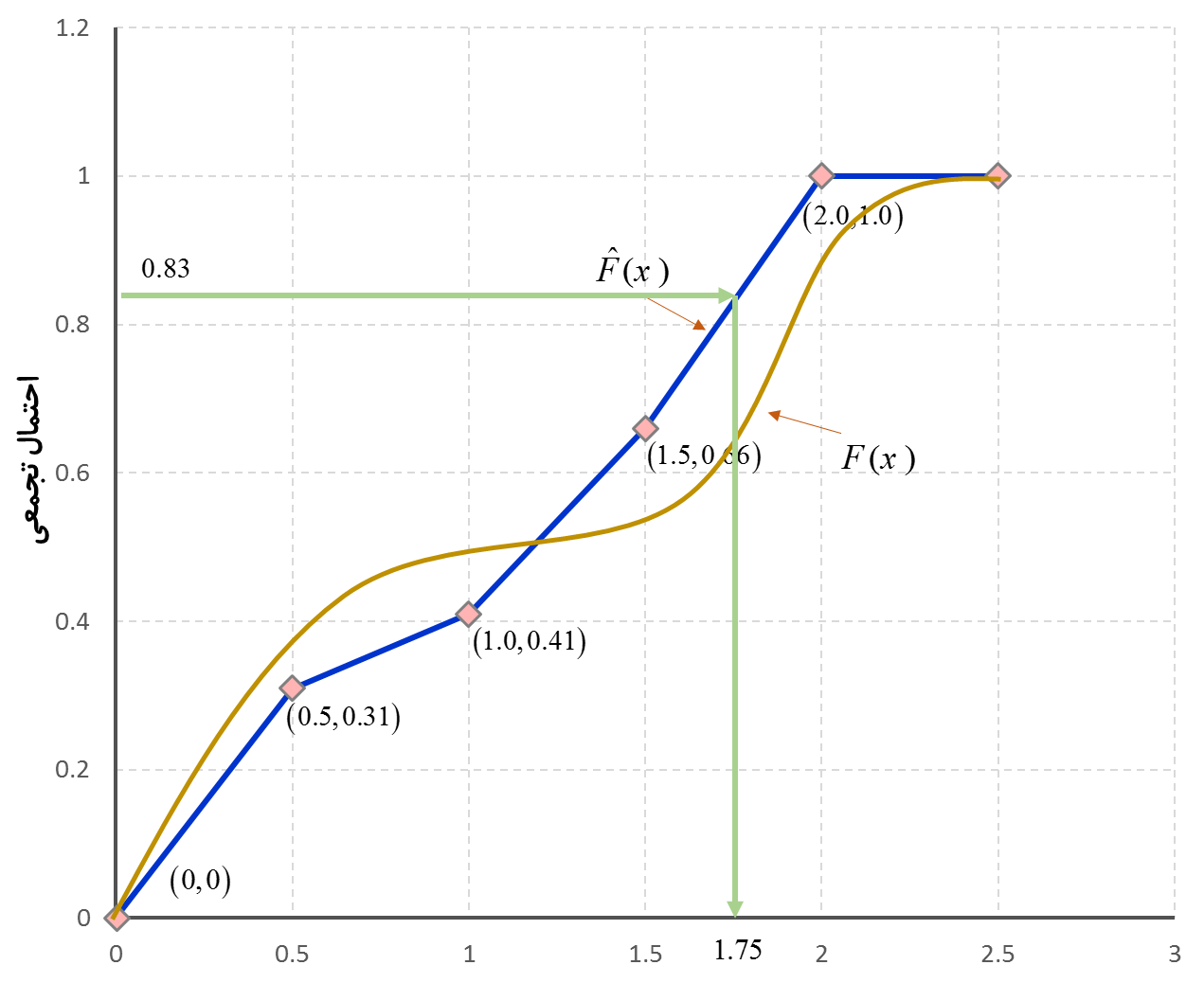
شکل حقیقی (F(x مجهول است و همواره در عمل، مجهول خواهد ماند مگر در صورتی که مقدار نامحدودی داده دسترس پذیر باشد. فرض بر این است که متغیر تصادفی X در مورد مدتهای نامنفی یا X≥0 صدق می کند. فرض کنید یک عدد تصادفی بین صفر و یک تولید میشود که برابر با R1=0.83 است. عدد تصادفی که دارای توزیع تجربی داده شده است به صورت زیر محاسبه میشود:
چون مقدار R1 بین دو عدد 0.66 و 1.0 است، مقدار X1 با درون یابی خطی مقدار بین 1.5 و 2.0 به صورت زیر بدست میآید.
در شکل زیر، نمایش شماتیک برای محاسبه مقدار عدد تصادفی با توزیع تجربی داده شده به صورت زیر میشود.