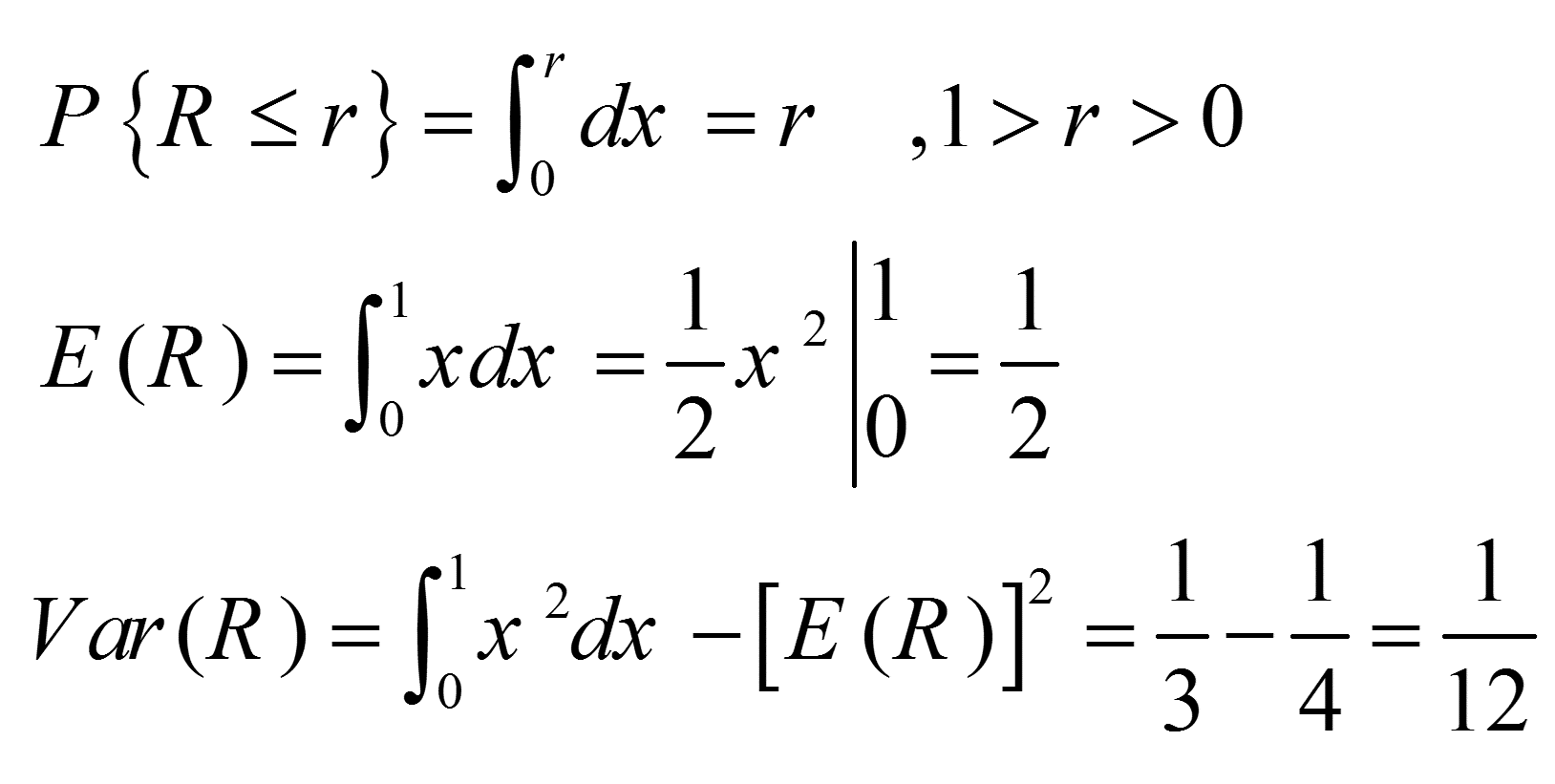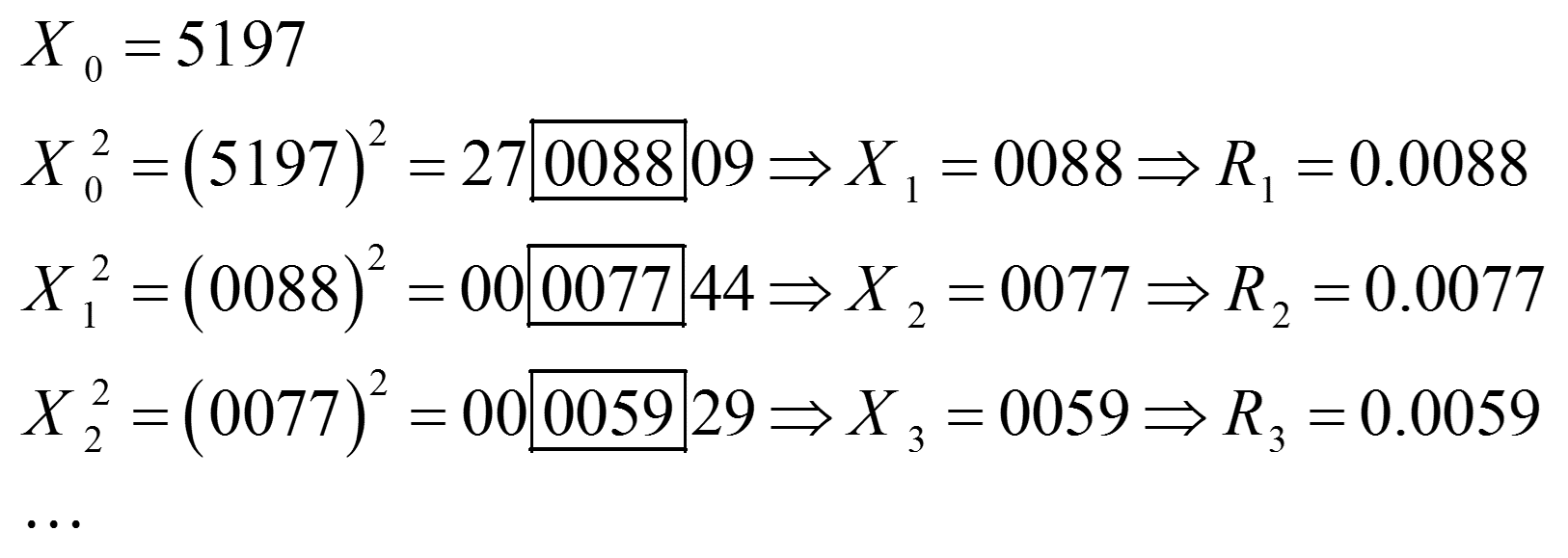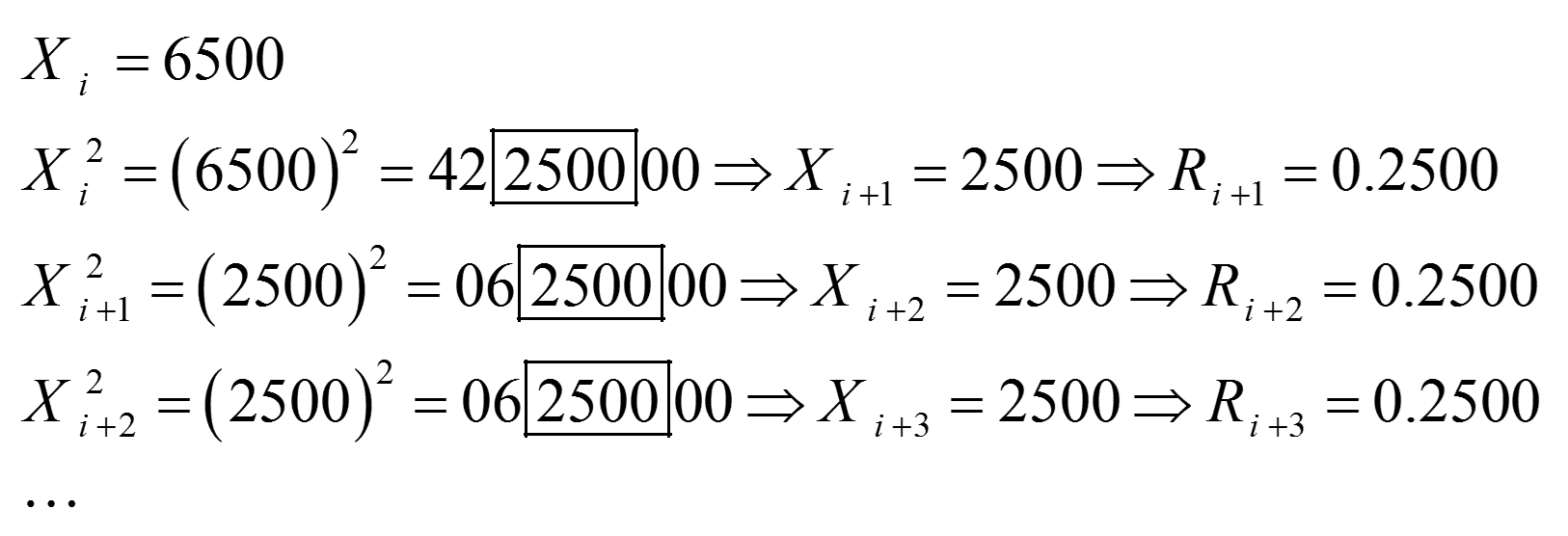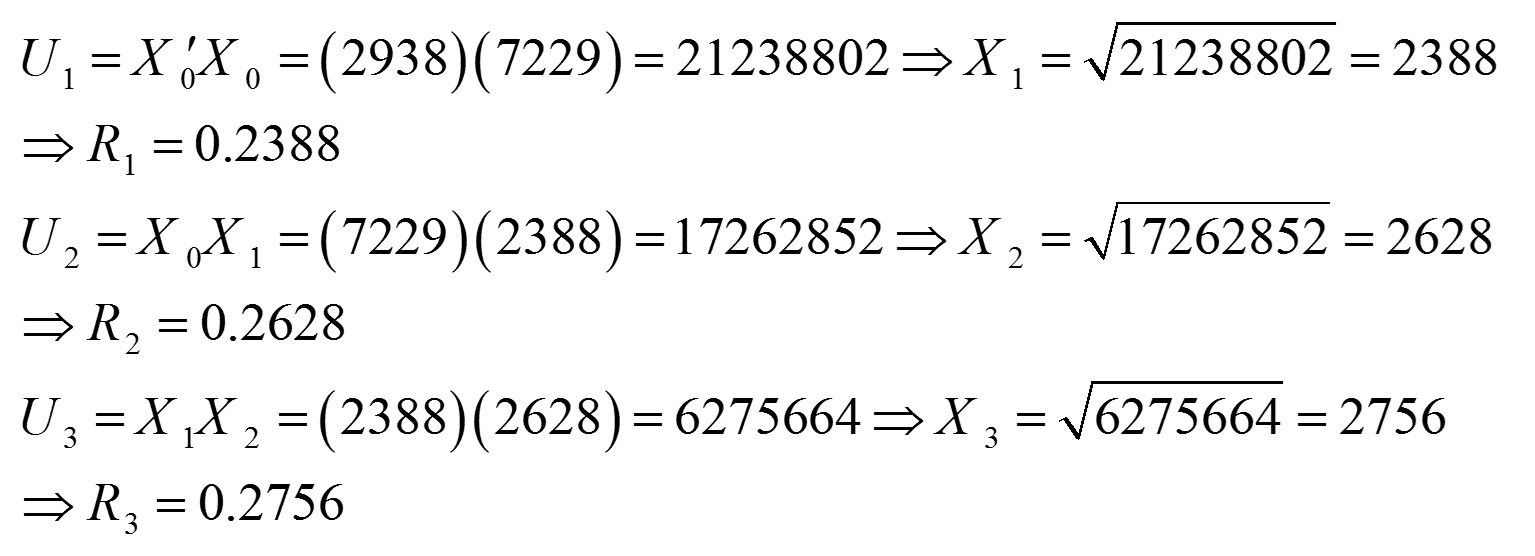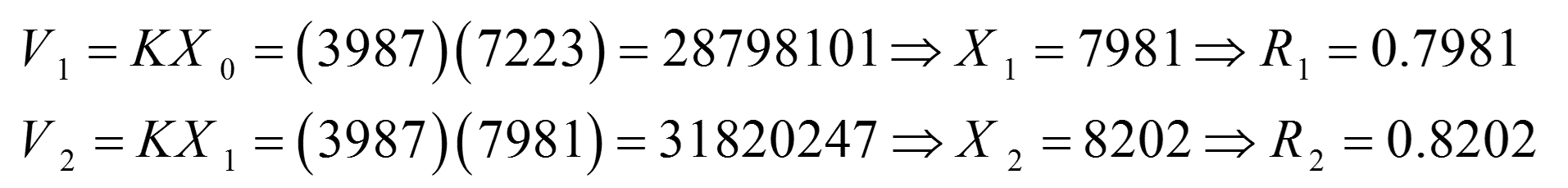درس 25: تولید اعداد تصادفی

تهیه شده توسط گروه بهینه یاب

آموزش روش های تولید اعداد تصادفی

مقدمه

آموزش روش های تولید اعداد تصادفی

روش‌های متفاوتی برای تولید اعداد تصادفی وجود دارد. تمام این روش ها یک وجه مشترک دارند: اینکه تمام آن ها از برنامه های کامپیوتری مولد دنباله اعداد استفاده می‌کنند به طوری که از لحاظ نظری اعداد مزبور در فاصله صفر تا یک توزیع یکنواخت دارند و از لحاظ آماری نیز هر عدد از سایر اعداد موجود در دنباله مستقل است.

در این درس به ارایه برخی از روش‌های محاسباتی تولید اعداد تصادفی می پردازیم، ضوابط ارزیابی، مقایسه و انتخاب را عرضه می‌داریم و سرانجام آزمایش های مربوط به تصادفی بودن اعداد به دست آمده از مولدهای را معرفی می‌کنیم.

خواص اعداد تصادفی

آموزش روش های تولید اعداد تصادفی

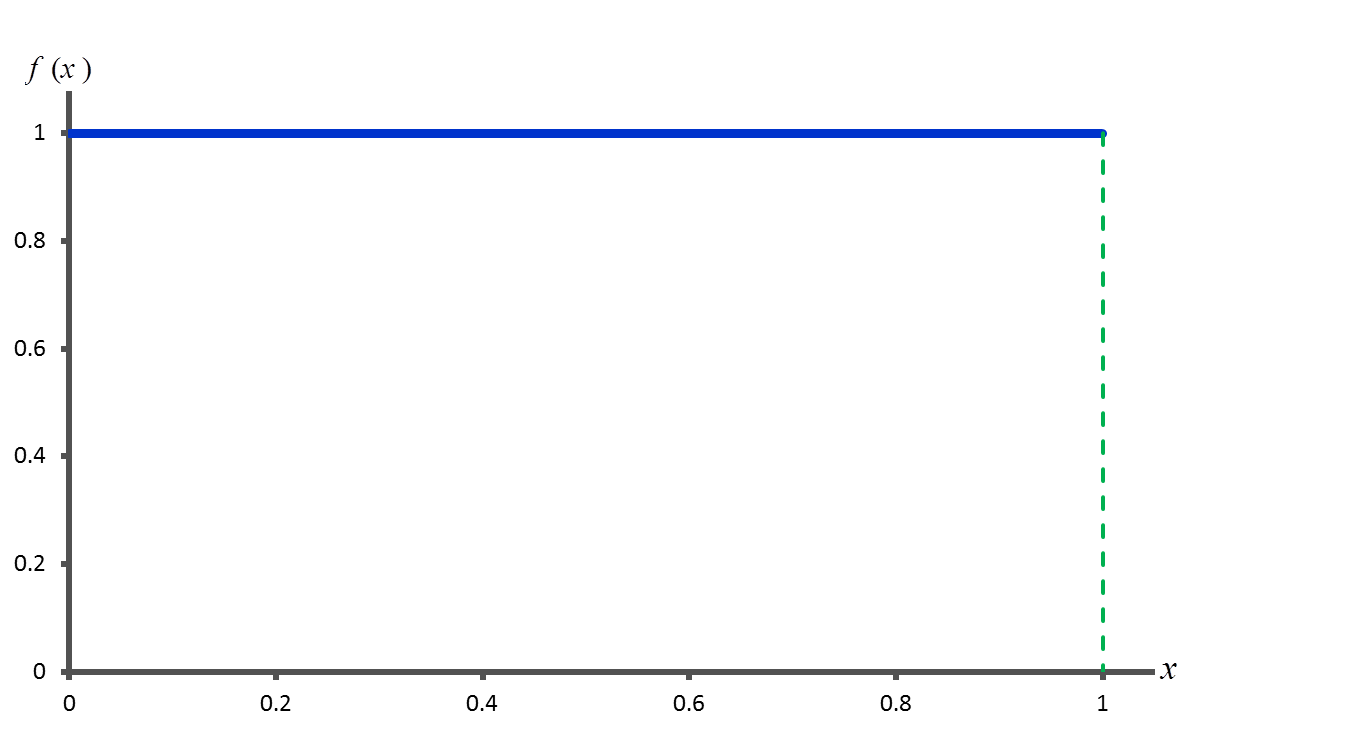
هر دنباله از اعداد تصادفی مانند R₁، R₂ و … باید دو خاصیت آماری مهم داشته باشد. این دو خاصیت عبارت از توزیع احتمال یکنواخت و استقلال است. هر عدد تصادفی مانند R_i نمونه مستقلی از توزیع احتمال یکنواخت و پیوسته با پارامترهای صفر و یک محسوب می شود. تابع چگالی این گونه متغیر تصادفی به صورت زیر تعریف می شود.

نمایش این تابع چگالی در شکل 1 نشان داده شده است.

تابع تجمعی، امید ریاضی، و واریانس R_i به ترتیب به صورت زیر محاسبه می شود.آموزش روش های تولید اعداد تصادفی

در باره پیامدهای خاصیت استقلال و خاصیت توزیع احتمال یکنواخت پیوسته برای اعداد تصادفی، می‌توان دو مورد زیر را بیان کرد:

1 – اگر فاصله (0,1) به n رده با زیر فاصله مساوی تقسیم شود، انتظار می رود که از N مشاهده N/n آن ها در هر رده قرار گیرد.

2 – احتمال حصول یک مشاهده در یک رده، مستقل از محل قرار گرفتن سایر مشاهده ها است.آموزش روش های تولید اعداد تصادفی

تولید اعداد شبه تصادفی

می‌بینیم که در عنوان این بخش از کلمه شبه به معنی غیرواقعی استفاده شده است. در واقع، منظور این نیست که در این بخش به تولید تصادفی غیرواقعی می پردازیم. مقصود از قید کلمه شبه تاکید بر این مطلب است که استفاده از یک روش قطعی و مشخص برای تولید اعداد تصادفی، امکان بالقوه تصادفی بودن واقعی را از بین می برد. در صورتی که روش مورد استفاده، قطعی و مشخص باشد، مجموعه اعداد تصادفی تولید شده توسط آن تکرار پذیر خواهد بود. پس، اعداد تولید شده واقعاً تصادفی نیست. اما باید توجه داشت هدف هر روش این است که به نحوی اعداد تصادفی در محدود صفر و یک تولید کند تا اعداد تولید شده در بالاترین حد ممکن دو خاصیت استقلال و توزیع یکنواخت را داشته باشد.آموزش روش های تولید اعداد تصادفی

به هنگام تولید اعداد شبه تصادفی، مسلما بروز مسائل یا ارتکاب خطاهایی قابل تصور است. این نوع مسائل یا خطاها به خواص استقلال و توزیع احتمال یکنواخت مربوط می شود. مثال هایی در این زمینه در زیر ارایه شده است:

آموزش روش های تولید اعداد تصادفی

1 – اعداد تصادفی ممکن است توزیع احتمال یکنواخت نداشته باشند.

2 – اعداد تصادفی ممکن است جدا از هم (نه پیوسته) باشد

3 – میانگین اعداد تولید شده ممکن است بیش از حد بزرگ یا بیش از حد متعارف کوچک باشد.

4 – واریانس اعداد تصادفی تولید شده ممکن است تفاوت قابل توجهی از مقدار متعارف داشته باشد.

5 – ممکن است دنباله اعداد تولید شده تغییراتی تناوبی از خود نشان دهد. بعضی از مثال ها عبارتند از:

الف) وجود همبستگی بین اعداد

ب) وجود رابطه مقداری بین اعداد مجاور به این ترتیب که اعداد مجاور روندی صعودی یا نزولی از خود نشان دهد.

ج) وجود چند عدد بزرگتر از میانگین و به دنبال آن وجود چند عدد کوچکتر از میانگین

به منظور کشف عدم استقلال و یا عدم پیروی اعداد بدست آمده از یک مولد از تابع چگالی یکنواخت، می توان از آزمون های معرفی شده که در این درس ارایه می شود استفاده کرد. اگر متعاقب انجام آزمون های مربوط مولدی غیرقابل قبول تشخیص داده شد باید به جستجوی مولد دیگری پرداخت.

تعداد روش های تولید اعداد (شبه) تصادفی فراوان است. از این بعد کلمه شبه را حذف می کنیم. قبل از تشریح برخی از روش های تولید اعداد تصادفی، بعضی از ملاحظات مهم را فهرست وارد ارایه می کنیم:

آموزش روش های تولید اعداد تصادفی

1 – روش یا الگوریتم تولید اعداد تصادفی باید سریع باشد. محاسبات شبیه سازی شاید آنقدر پرهزینه نباشد ولی جمع محاسبات لازم در یک بررسی شبیه سازی ممکن است قابل توجه باشد. در این صورت باید به جستجوی الگوریتمی پرداخت که هزینه تولید در مورد آن بسیار کم باشد.

2 – روش نباید نیاز به مقدار زیادی حافظه کامپیوتری داشته باشد. اشغال حافظه ممکن است بسیار پر هزینه باشد و بر انجام بخش های دیگر بررسی شبیه سازی از لحاظ نیاز به حافظه تاثیر منفی بگذارد.

3 – طول دنباله اعداد تولید شده باید به اندازه کافی بلند باشد. منظور از طول دنباله، تعداد اعدادی است که بدون تکرار دنباله در آن قرار می گیرد. حالت خاصی از تکرار دنباله ناظر به از هم پاشیدن الگوریتم است. اگر عدد تصادفی معینی به طور مکرر تولید شود می گویند الگوریتم از هم پاشیده است. این امر در یکی از مثال های بخش بعد توضیح داده شده است.

4 – صرفنظر از وضعیت سیستم در دست شبیه سازی، باید بتوان با تعیین نقطه شروع، الگوریتم مولد را در تولید مجموعه مشخصی از اعداد تصادفی به کار گرفت. رعایت این امر در بررسی های شبیه سازی لازم است و از آن برای تسهیل مقایسه دو سیستم استفاده می شود.

5 – اعداد تصادفی تولید شده باید تا حدود زیادی از خواص آماری توزیع یکنواخت و استقلال برخوردار باشد.

روش های مختلف تولید اعداد تصادفیآموزش روش های تولید اعداد تصادفی

روش های رایج تولید اعداد تصادفی در این بخش بررسی می شود.

روش میان مربعی

این روش با یک عدد اولیه به نام هسته شروع به کار می کند. روال کار چنین است که هسته را مربع می‌کند و ارقام میانی آن را تعیین و پس از نوشتن صفر و ممیز در سمت چپ ارقام میانی، اولین عدد تصادفی را تولید می کنند. به منظور تولید عدد تصادفی دوم، باید ارقام میانی در مرحله قبل را مربع، ارقام میانی حاصل را تعیین و به عدد اعشاری تبدیل کرد و همین روند ادامه پیدا می کند. اگر هسته n رقمی باشد، مربع آن 2n-1 یا 2n رقمی خواهد بود و اگر n زوج باشد با حذف n/2 ارقام از هر سمت (راست و چپ) مربع آن، می توان ارقام میانی را تعیین کرد.

مثال 1: فرض کنید که به دنباله از اعداد تصادفی چهار رقمی نیاز داریم. هسته را با X₀ نماد گذاری کنید و مقدار 5497 را برای آن در نظر بگیرید. فرض کنید i-امین عددی که مربع می شود X_i و i امین عدد تصادفی که تولید می شود R_i باشد.آموزش روش های تولید اعداد تصادفی

نکته: این روش می تواند دچار مشکلاتی شود. اولا نمی‌توان قواعد ساده‌ای برای تعیین مقدار هسته ارایه کرد که عملکرد مطلوب الگوریتم را تضمین کند. همچنین، با ظهور رقم صفر در سمت چپ ارقام میانی، دنباله اعداد تصادفی تولید شده به سرعت به انتها می رسد. در روشن شدن این موضوع به مثال زیر توجه کنید.

مثال 2: فرض کنید که هسته مثال 1 به 5197 تغییر کند. در این صورت:

می‌بینیم که تمام R_i ها با صفر شروع می شود.

روش فوق عیب دیگری هم دارد که از هم پاشیدگی شدن آن است. از هم پاشیده شدن الگوریتم به خاطر حصول مقداری تکراری یا مقدار صفر برای ارقام میانی است.

مثال 3: تصور کنید که به هنگام استفاده از روش میان مربعی، مقدار 6500 برای یکی از X ها تولید شده است. در این صورت، به ازای n=4 داریم:

با ثابت ماندن مقدار اعداد تصادفی تولد شده، الگوریتم عملا از هم می‌پاشد.

روش میان ضربی

این روش همانند روش میان مربعی است و با انتخاب دو هسته، X₀ و X’₀ که تعداد ارقامشان مساوی است شروع می شود. اگر دو هسته n رقمی باشد، آن ها را در هم ضرب می‌کنیم. با حذف n/2 از ارقام سمت راست و همین تعداد رقم از سمت چپ حاصلضرب، n رقم قرار گرفته در وسط را تعیین و آن را تبدیل به یک عدد اعشاری کوچکتر از یک می‌کنیم. اگر n رقم قرار گرفته در وسط حاصل ضرب با X₁ نماد گذاری شود، به منظور تولید عدد تصادفی دوم، محاسبات فوق را با X₀ و X₁ تکرار می‌کنیم. این روند تکرار می شود. برای روشن شدن موضوع مثال زیر را در نظر بگیرید.

مثال 4: از دو هسته X₀=7229 و 2938= X’₀ استفاده و براساس روش میان ضربی، اعداد تصادفی چهار رقمی تولید کنید.

نکته: این روش شباهت بسیاری به روش میان مربعی دارد. طول دنباله برای این روش بلندتر و یکنواختی توزیع اعداد تولید شده بیشتر است. به هر صورت، این روش نیز عیب عمده ی از هم پاشیده شدن را دارد.

روش مضرب ثابت

این روش تفاوت ناچیزی با روش میان ضربی دارد. در واقع، با ثابت نگه داشتن یکی از دو عددی که در روش قبل در یکدیگر ضرب می شد می توان اعداد را تولید کرد. فرض کنید عدد ثابت را با K نماد گذاری می‌کنیم و تعداد ارقام K و X₀ را یکسان در نظر می‌گیریم. تحت این شرایط، تمام محاسبات مانند روش میان ضربی انجام می گیرد.

مثال 5: با استفاده از دو هسته K=3987 و X₀=7223 و براساس روش مضرب ثابت، دنباله ای از اعداد تصادفی چهار رقمی تولید کنید.

این روش همان معایب روش میان ضربی را دارد. عملکرد مناسب این روش تا حد زیادی به انتخاب مقدار ثابت K بستگی دارد.