حل مسائل بهینه سازی به روش الگوریتم جستجوی ممنوعه
برای دانلود خلاصه آموزش روش جستجوی ممنوعه لطفا ایمیل خود را وارد کنید تا این آموزش برای شما ارسال شود. این آموزش شامل فیلم، جزوه، پادکست و فایل ارایه است.
درس 15: الگوریتم جستجوی ممنوعه
تهیه شده توسط گروه بهینه یاب
مقدمه
محاسبه راه حل بهینه یا Optimal solution برای اکثر مسایل بهینه سازی که در خیلی از زمینههای کاربردی و عملی مشاهده میگردند، کار دشوار و سختی است. در عمل، معمولا به راه حلهای خوب که از الگوریتمهای هیوریستیک Heuristic یا متاهیوریستیک (همان فراابتکاری) Metaheuristic بدست میآید، اکتفا میگردد. متاهیوریستیکها مجموعه ای از فنون بهینه سازی تقریبی Approximate optimization techniques را که عمدتا در طول دو دهه گذشته شهرت پیدا کرده اند، در بر میگیرند. روشهای فراابتکاری راه حلهای قابل قبول در زمان معقول را برای مسایل پیچیده و سخت، در زمینههای مهندسی و علوم پایه ارایه می نمایند. برخلاف الگوریتمهای بهینه سازی دقیق Exact optimization algorithms ، فراابتکاری ها بهینه بودن جوابهای بدست آمده را ضمانت نمی نمایند.
کلمه متاهیوریستیک از کلمه یونانی “Heuriskein” به معنای هنر کشف قواعد جدید برای حل مسایل گرفته شده است. پیشوند “متا” نیز از یک کلمه یونانی به معنای “متدولوژی” سطح بالا گرفته شده است. واژه ” متاهیوریستیک ” اولین بار توسط گلوور در سال 1986 ارایه گردید. روش جستجوی متاهیوریستیک را می توان به صورت متدولوژیهای عمومی سطح بالایی که می توانند به عنوان یک استراتژی راهنما در طراحی هیورستیکهای اختصاصی برای حل مسایل بهینه سازی تخصصی به کار روند، تعریف کرد.
برخلاف روشهای دقیق، متاهیوریستیکها (فراابتکاریها) برای مسایل با اندازههای بزرگ کاربرد دشوار دارد و راه حلهایی راضی کننده ای در زمان معقولی ارایه می نمایند. در این الگوریتمها، هیچ گونه ضمانتی برای یافتن جواب بهینه سراسری یا حدودی از آن وجود ندارد. متاهیوریستیکها (فراابتکاریها) در طول بیست سال گذشته شهرت زیادی پیدا کرده اند. کاربرد و استفاده از آنها در خیلی از مسایل، کارایی و اثر بخشی آنها را برای حل مسایل پیچیده و بزرگ نشان می دهد. فراابتکاریها در خیلی از زمینهها از قبیل موارد زیر کاربرد دارند:
- طراحی مهندسی، بهینه سازی توپولوژی، بهینه سازی مسایل الکترونیک، آئرودینامیک، دینامک سیالات، مخابرات، رباتیک
- یادگیری ماشین و کاوش دادهها
- مدل سازی سیستمها، شبیه سازی و تحقیق در شیمی، فیزیک، بیولوژی، کنترل، سیگنال، و پردازش تصویر
- مسایل مسیردهی و برنامه ریزی، برنامه ریزی ربات، مسایل تولید و زمان بندی، حمل و نقل و لجستیک، مدیریت زنجیره تامین
روشهای مختلف الگوریتمهای فراابتکاری یا متاهیوریستیک تا به حال پیشنهاد شده است که به صورت زیر است:
- بهینه سازی کلونی مورچگان Ant colony optimization
- بهینه سازی کلونی زنبوران Bee colony
- الگوریتمهای ترتیبی cultural algorithms
- الگوریتمهای با هم تکاملی Co-evolutionary algorithms
- الگوریتم ژنتیک Genetic algorithm
- جستجوی محلی تکراری Iterated local search
- بهینه سازی توده ذرات particle swarm intelligent
- انجماد تدریجی Simulated Annealing
- جستجوی ممنوع Taboo search
- جستجوی همسایگی متغیر Variable neighboar search
در طراحی یک فراابتکاری، دو معیار متناقض شامل کاوش (Exploration) و در فضای جستجو (گوناگونی و تنوع) و تبعیت (Exploitation) از بهترین راه حلهای پیدا شده، باید در نظر گرفته شوند. در کاوش در ناحیههای جستجو نشده بررسی صورت میگیرد. در تبعیت، در ناحیههای امید بخش که تا به حال در آن ناحیه یک جواب خوب پیدا شده است بررسی بیشتر صورت میگیرد. در صورتیکه به کاوش اهمیت بیشتری داده شود، الگوریتم رفتار تصادفی بیشتری خواهد داشت و به سمت رفتار تصادفی میل می کند و در صورتی که به رفتار تبعیت توجه بیشتری شود، الگوریتم از رفتار تصادفی فاصله میگیرد و جستجو تنها در محدوده راه حلهای خوب به جستجو می پردازد. حل مسائل بهینه سازی به روش الگوریتم جستجوی ممنوعه
معیارهای طبقه بندی زیادی ممکن است برای طبقه بندی فراابتکاریها استفاده شود که در زیر به بعضی از آنها اشاره میشود:
الهام گرفته از طبیعت در مقابل عدم الهام از طبیعت
خیلی از الگوریتمهای فراابتکاری از فرایندههای طبیعی الهام گرفته شده اند: از قبیل الگوریتمهای اجتماع مورچگان و زنبور عسل که از هوش توده ای از گونههای مختلف مورچگان و زنبوران استفاده می کنند.حل مسائل بهینه سازی به روش الگوریتم جستجوی ممنوعه
نحوه استفاده از حافظه
بعضی از الگوریتمهای فراابتکاری از قبیل انجماد تدریجی بدون حافظه هستند و حرکتهای قبلی را در جایی ذخیره نمی کنند. در مقابل الگوریتم انجماد تدریجی از یک حافظه که بعضی از اطلاعات را در طول جستجو بدست میآورد، ذخیره می کند.
قطعی در مقابل احتمالی
یک الگوریتم قطعی، یک مسئله بهینه سازی را از طریق تصمیم گیری قطعی حل می نماید(برای مثال الگوریتم جستجوی محلی و جستجوی ممنوع). در الگوریتمهای فراابتکاری احتمالی، بعضی از قواعد احتمالی در فرایند جستجو مورد استفاده قرار میگیرد که می توان به الگوریتم انجماد تدریجی و الگوریتم ژنتیک اشاره کرد. در الگوریتمهای قطعی، با داشتن یک راه حل اولیه و اجراهای متفاوت، تنها یک جواب نهایی بدست میآید و در حالی که در الگوریتمهای تصادفی، با داشتن یک راه حل اولیه و اجراهای متفاوت، ممکن است که جوابهای نهایی متفاوتی بدست آید.
تکراری در مقابل حریصانه
در الگوریتمهای تکراری، الگوریتم با یک راه حل کامل شروع شده و در هر تکرار راه حل یا راه حلها تغییر پیدا می کنند. در الگوریتمهای حریصانه یک راه حل کامل در اختیار نبوده بلکه با یک راه حل ساخته نشده شروع شده و در هر مرحله، یک متغیر تصمیم از مسئله یک قسمت از راه حل را می سازد. اغلب الگوریتمهای فراابتکاری، الگوریتمهای تکراری هستند.
در ادامه الگوریتم جستجو ممنوع که الگوریتمی است که از طبیعت الهام گرفته است و در رده الگوریتمهای قطعی، و تکراری با حافظه قرار میگیرد صحبت میشود.
الگوریتم جستجوی ممنوعه
الگوریتم جستجو ممنوعه یا الگوریتم جستجوی ممنوع Taboo search اولین بار توسط فرد گلوور در مقاله ای که در سال 1986 منتشر گردید، ارایه شد. همچنین بعدا دو مقاله از ایشان با نام ساده “جستجو ممنوع” در سالهای 1989 و 1990 منتشر گردید که در آن، خیلی از کاربردهای جستجو ممنوع را معرفی کرد.
اساس نامگذاری این روش، استفاده آن از لیستی به نام لیست ممنوع Tabu listمی باشد. این لیست برای جلوگیری از افتادن الگوریتم در نقطه بهینههای محلی طراحی شده است. به طور خلاصه، این روش به صورت مقابل بیان میشود. این الگوریتم از یک نقطه یا راه حل شروع کرده و در اطراف آن نقطه، به جستجوی همسایگی می پردازد. در بین همسایهها، بهترین را انتخاب و به آن نقطه حرکت می نماید. این جستجوی را تا زمانی ادامه می دهد که یک معیار توقف برآورده گردد. در پایان جستجو، نقطه بهینه گزارش میشود. این الگوریتم فراابتکاری برای جلوگیری از افتادن در بهینه محلی، از یک حافظه کوتاه مدت استفاده می نماید. وظیفه این حافظه کوتاه مدت نگهداری از آخرین حرکتها است که تعداد آنها محدود شده است. این حرکتها در یک لیست (لیست ممنوع) نگهداری میشوند. در هر حرکت، در صورتی که حرکت در لیست ممنوع قرار گرفته باشد، از آن انتقال جلوگیری میگردد مگر آنکه حرکت ممنوع دارای شرایط خاصی باشد.
اصول کلی الگوریتم جستجوی ممنوعه
الگوریتم فراابتکاری جستجوی ممنوع را می توان به عنوان یک استراتژی جستجوی محلی در نظر گرفت. این جستجو شامل حرکت از یک محل ( همان جواب یا نقطه) به راه حل دیگری در همسایگی او مطابق با بعضی از قواعد تعریف شده می باشد. برای مثال، مسئله حداقل سازی یک تابع همچون (F(x روی یک مجموع محدود از نقاط X را به عنوان یک حالت عمومی از یک مساله بهینه سازی ترکیبی در نظر بگیرید. روش جستجوی ممنوع از یک راه حل اختیاری شروع شده و در هر مرحله، به جستجوی همسایگی می پردازد. در این جستجو همسایگی، به هر یک زیر مجموعه اختصاص داده میشود که همسایه x نامیده میشود. در مرحله n، یک راه حل جدید در همسایگی از راه حل جاری را انتخاب می نماید. معمولا این راه حل بهترین راه حل در بین همسایهها بوده و دارای شرط زیر می باشد.
الگوریتم، بعد از انتخاب راه حل xn+1 از نقطه xn به xn+1 حرکت می نماید و آنگاه راه حل xn+1 به عنوان راه حل جاری بعدی شناخته میشود. این جستجو تا زمانی ادامه می یابد که یک شرط توقف تعریف شده برآورده شود.
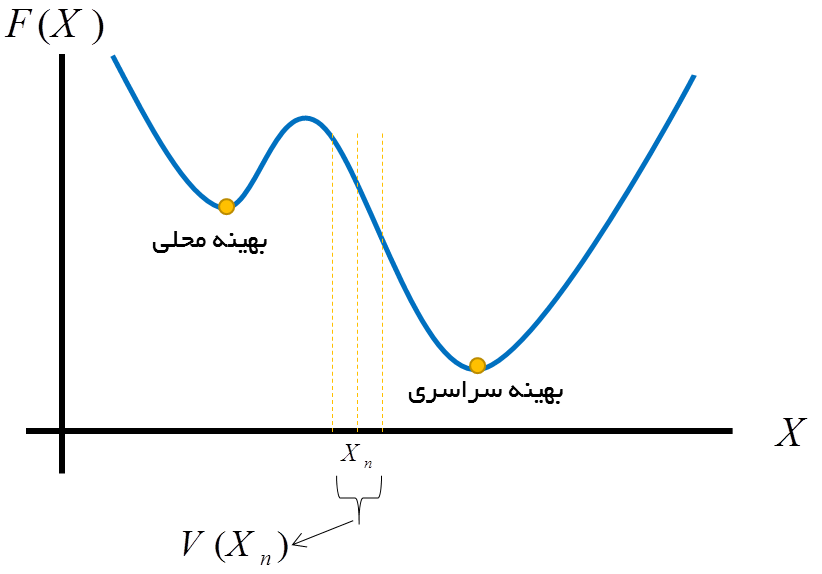
ممکن است به هنگام حرکت از یک نقطه به نقطه دیگر مشکلی پیش آید که به نام افتادن در بهینه محلی معروف است. شکل زیر را در نظر بگیرید.
همان طور که در این شکل دیده میشود، فضای جواب مساله دارای دو نقطه مینیم یا بهینه می باشد. نقطه بهینه، نقطه ای تعریف میشود که آن نقطه بهترین نقطه در تمامی نقاط اطراف خود باشد. به عبارت دیگر، نقطه ای مینیمم است که تمامی راه حلهای اطراف آن بدتر از خود آن باشند. در این شکل، یک نقطه بهینه محلی و یک نقطه بهینه سراسری نمایش داده شده است.
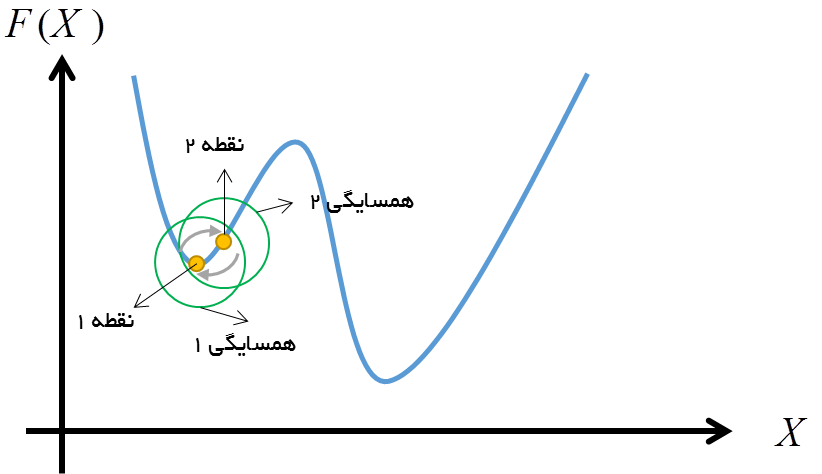
مشکل افتادن در بهینه محلی، زمانی اتفاق می افتد که الگوریتم به نقطه بهینه محلی میرسد. در این نقطه، الگوریتم به جستجوی همسایگی پرداخته و یک همسایه را انتخاب می نماید. لازم به توضیح است که الگوریتم در جستجوی همسایگی، حتما باید یک نقطه را از بین همسایگان و غیر از خود انتخاب کند و به آن نقطه حرکت نماید، حتی اگر کیفیت آن نقطه پایین تر باشد. زمانی که الگوریتم در بهینه محلی قرار دارد، نقاط همسایه او دارای مقدار تابع یا کیفیت بدتر از خود نقطه بهینه محلی می باشند. از روی اجبار، الگوریتم به یکی از نقطه بین آنها انتقال می یابد. بعد از حرکت به آن نقطه، دوباره به جستجوی همسایگی می پردازد و با توجه به اینکه نقطه بهینه محلی قبلی در همسایگی نقطه جدید قرار دارد و از نقطه فعلی بهتر است مجددا به بهینه محلی بر میگردد. در این حالت الگوریتم در یک دور یا سیکل افتاده و از آن خارج نمیگردد. این وضعیت به افتادن در بهینه محلی معروف می باشد که در شکل زیر نشان داده میشود.
در این شکل بهینه محلی با نقطه 1 نمایش داده شده و همسایه انتخاب شده برای حرکت، نقطه 2 می باشد. بعد از حرکت به نقطه 2، بهترین نقطه در همسایگی او، نقطه 1 می باشد و به آن بر میگردد. این روند همواره تکرار شده و الگوریتم از این دور یا سیکل خارج نمیگردد.
الگوریتم جستجوی ممنوع برای جلوگیری از این مشکل از ابزار لیست ممنوع استفاده می کند. در هر مرحله، در هنگام حرکت از یک نقطه به نقطه دیگر، مشخصاتی از حرکت (برای مثال فاصله و جهت) را به حافظه سپرده و در نقطه جدید از انجام حرکتی که منجر به برگشت به عقب میشود خودداری می کند. به منظور کارایی بیشتر، به جای یک حرکت قبلی، مجموعه ای از حرکتهای قبلی را به حافظه سپرده و آنها در لیستی به نام لیست ممنوع ذخیره می نماید. این لیست پویا بوده و در طول الگوریتم به هنگام میگردد. به عبارت دیگر، در هر حرکت، مشخصه حرکت جدید وارد لیست شده و مشخصه حرکتهای قدیمی از لیست حذف میگردد. یک قاعده ساده این است که لیست طول محدودی داشته و زمان ورود یک حرکت به لیست، قدیمی ترین حرکت از آن خارج گردد.
الگوریتمها در هر مرحله، بهترین نقطه را در بین همسایگان جستجو نموده و در صورتی به آن نقطه حرکت می نماید که آن حرکت ممنوع نباشد. به عبارت دیگر، حرکت مدنظر را با لیست ممنوع مقایسه نموده و در صورتی که حرکت ممنوع باشد، از آن حرکت صرفه نظر نموده و بهترین حرکت بعدی را در بین همسایگان انتخاب می نماید. نقطه بعدی انتخاب شده نیز با لیست ممنوع مقایسه میگردد.
لیست ممنوع با وجود مقید بودن، محدودیتهایی را برای الگوریتم به وجود میآورد. در طول جستجو الگوریتم، ممکن است یک حرکت ممنوع باشد، ولی انجام حرکت با وجود ممنوع بودن تاثیر بالایی در بهبود جهت حرکت و کیفیت جواب های الگوریتم دارد. برای این منظور، الگوریتم از یک معیار به نام معیار آرمانی برای رهایی از این محدودیت در مواقع لزوم استفاده می نماید. یک معیار آرمانی ساده این است که ممنوعیت حرکتی که موجب رسیدن به نقطه ای گردد که از تمامی نقاطی که تاکنون بدست آمده است بهتر باشد، در نظر گرفته نمیشود.
قاعده توقف پایان الگورتیم جستجو را تعیین می کند. یک قاعده ساده می توان به صورت محدودیتی برای کل تعداد حرکتها باشد. به عبارت دیگر، وقتی تعداد حرکتها به عدد خاصی رسید الگوریتم متوقف گردد.
توجه: برای مطالعه ادامه این درس شامل بیان ریاضی الگوریتم فراابتکاری جستجوی ممنوع و حل یک مثال با استفاده از این روش، جزوه آموزشی این درس را دانلود کنید.
حل مسائل بهینه سازی به روش الگوریتم جستجوی ممنوعه