نظریه بازی و روش های حل نظریه بازی به همراه تمرین با حل تشریحی

درس 14: نظریه بازی

تهیه شده توسط گروه بهینه یاب

مقدمه

زندگی مملو از تضادها و مبارزات است. نمونه های بسیاری را می توان بیان کرد که طرف های درگیر منافع متضاد و خلاف هم دارند. جنگ ها، مبارزات سیاسی، بازاریابی و قمارها ازجمله این مجادله ها هستند. یک ویژگی اساسی این مجادله ها این است که نتیجه نهایی بستگی به مجموعه سیاست هایی (Strategy) دارد که توسط طرفین درگیر اخذ می گردد. نظریه بازی یا Game Theory، نظریه ای ریاضی است که به بررسی مشخصه های کلی رقابت ها می پردازد و در این نظریه بر فرایند تصمیم گیری طرفین مخاصمه تاکید می کند.

بازی های ریاضی انواع مختلفی دارد که در ادامه به اختصار بیان می شود.

بازی های غیرمشارکتی و بازی های مشارکتی (Non-cooperative and Cooperation Games)

در نظریه بازی در بازی های غیرمشارکتی فرض بر این است که هیچ گونه تبادل اطلاعات، همکاری، توافق و تعهد ما بین بازیکنان قبل یا حین بازی وجود ندارد. هر بازیکن جهت رسیدن به هدف خودش بر طبق قوانین بازی، بازی می کند و سایر بازیکنان رقبای وی محسوب می شوند.

در بازی های مشارکتی بازیکنان امکان تبادل اطلاع یا همکاری تعهد آور قبل یا حین بازی را دارند که موجب می شود برخی یا تمام بازیکنان که در توافق مشارکت دارند ملزم به رعایت آن باشند و در راه رسیدن به اهداف توافق تلاش می کنند. از جمله بازی های مشارکتی می توان به اوپک اشاره کرد.

بازی های همزمان و بازی های دنباله ای (Simltaneous and Sequential Games)

در نظریه بازی در بازی های همزمان بازیکنان همزمان با هم تصمیم می گیرند، اما در بازی های دنباله ای بازیکن آخری از نحوه تصمیم بازیکن(یا بازیکنان) قبلی مطلع است.

از جمله بازی های همزمان می توان به بازی سنگ-کاغذ-قیچی و از جمله بازی های دنباله ای می توان به بازی شطرنج اشاره کرد.

بازی با اطلاعات کامل/غیرکامل/یا بدون اطلاعات (Games with Perfect/Imperfect information)

در نظریه بازی در بازی با اطلاع کامل، بازیکن اشراف کاملی در لحظه انجام بازی از تصمیمات بازیکنان دیگر دارد. اما در بازی با اطلاعات غیرکامل بازیکن فقط بخشی از اطلاعات مربوط به کل بازی را تا لحظه مورد نظر دارد. اگر اطلاعات در بازی کامل باشد فقط می توان بازی دنباله ای را انجام داد.

بازی های دونفره و n نفره (n>2)

در این بازی، دو یا بیش از دو نفر در بازی نقش دارند و از نوع غیر مشارکتی هستند. در این درس به طور خاص به یک نوع خاص از این نوع بازی با عنوان بازی دو نفره جمع صفر می پردازیم.

در نظریه بازی در بازی های دو نفری جمع صفر یا Two Person-Zero Sum Game ، دو بازیگر حضور دارند که یکی از بازیگرها، بازیگر 1 یا بازیگر سطری و دیگری بازیگر 2 یا بازیگر ستونی هستند. بازیگر 1 تنها مجاز به انتخاب یکی از سیاست ها از بین m سیاست خود است. به طور مشابه بازیگر 2 یا بازیگر ستونی مجاز به انتخاب یکی از n سیاست است.

علت جمع صفر خواندن این بازی آن است که مقدار برد یکی دقیقا با میزان باخت بازیگر دوم مساوی است و جمع جبری برد خالص هر دو بازیگر برابر صفر است.

اگر بازیگر 1 یا بازیگر سطری i-امین سیاست خود و بازیگر 2 یا بازیگر ستونی نیز j-امین سیاست خود را انتخاب کند، بازیگر 1 مقدار دریافت (برد) و بازیگر 2 نیز مقدار را پرداخت (باخت) می کند. دریافتی یک بازیگر از محل پرداخت بازیگر دیگر امکان پذیر است و به همین خاطر بازی را مجموع صفر (Zero-sum) می نامیم زیر حاصل جمع دریافت ها و پرداخت های بازیگران صفر است و منافع دو بازیگر کاملا در تضاد با هم باشند.

در نظریه بازی ماتریس پرداخت یا بازده (Pay-off Matrix) در این نوع بازی ها معمولا از دید بازیگر 1 یا بازیگر سطری نوشته می شود. اگر a_ij>0 یعنی بازیگر 1 واحد را از بازیگر 2 دریافت می کند و اگر a_ij<0 یعنی بازیگر 1 واحد به بازیگر 2 پرداخت می کند. ماتریس پرداخت یا بازده به صورت زیر می شود.

برای روشن شدن موضوع یک مثال می زنیم. دو بازیگر در یک بازی همزمان با یکدیگر یک یا دو انگشت خود را نشان می دهند. اگر تعداد انگشتان آن ها مساوی باشد، بازیگر اول مقدار یک دلار را به بازیگر دوم می پردازد و در غیر این صورت، بازیگر دوم باید یک دلار را به بازیگر اول بپردازد. به این ترتیب، هر بازیگر می تواند یکی از دو سیاست زیر را اتخاذ نماید.

• یک انگشت خود را نشان دهد.
• دو انگشت خود را نشان دهد.

جدول زیر بازده بازیگر اول بر حسب دلار را در صورت انتخاب هر یک از سیاست ها نشان می دهد.

نکته: در نظریه بازی، سیاست قاعده ای از پیش تعیین شده است که مشخص می کند هر بازیگر در تقابل هر پیش آمد که در هر یک از مراحل می تواند رخ دهد، چه واکنشی باید داشته باشد و هر بازیگر قبل از شروع بازی سیاست هایی که خود و طرف مقابل می تواند اتخاذ نماید را تعیین کرده و جدول بازده را از دیدگاه خود بدست می آورد.

نظریه بازی بر مبنای دو فرض استوار است.

• هر دو بازیگر عاقل و منطقی هستند و هر دو بازیگر نهایت توان خود را در مصاف حریف به کار می بندد تا بهترین نتیجه دست یابد.
• هر بازیگر در هنگام انتخاب سیاست خود فرض می کند که رقیب وی با فهمیدن این سیاست چه سیاستی را انتخاب می کند.

مثال: دو سیاست مدار در یک مبارزه انتخاباتی در مقابل یکدیگر قرار دارند. برای دو روز آخر قبل از انتخابات که از اهمیت بسزایی برخوردار است باید برنامه مبارزاتی تهیه شود. هر دو سیاست مدار می خواهند دو روز باقی مانده را در دو شهر (الف) و (ب) بگذرانند. آن ها می توانند در هر شهر یک روز یا در یک شهر دو روز به سر برند. هر سیاست مدار از برنامه حریف تا وقتی که اعلام نشود بی اطلاع است.

این دو رقیب از مدیران برنامه خود در این دو شهر خواسته اند تا اثرات تصمیم خود و رقیب را در مورد گذراندن یک یا دو روز در این دو شهر بر حسب پیش بینی افزایش یا کاهش تعداد رای بیابند.

برای اینکه این مسئله در غالب یک بازی دو نفری – جمع صفر فرموله شود. در ابتدا باید دو طرف بازی ( که در این جا دو سیاست مدار هستند) سیاست های هر کدام و همچنین جدول بازده تعیین شود.

هر یک از سیاست مداران سه سیاست پیش رو دارند.

• سیاست1: گذراندن یک روز در هر شهر
• سیاست 2: گذراندن هر دو روز در شهر (الف)
• سیاست 3: گذراندن هر دو روز در شهر (ب)

سه گونه جدول بازده برای این مسئله به صورت زیر تعریف می شود.

گونه اول:

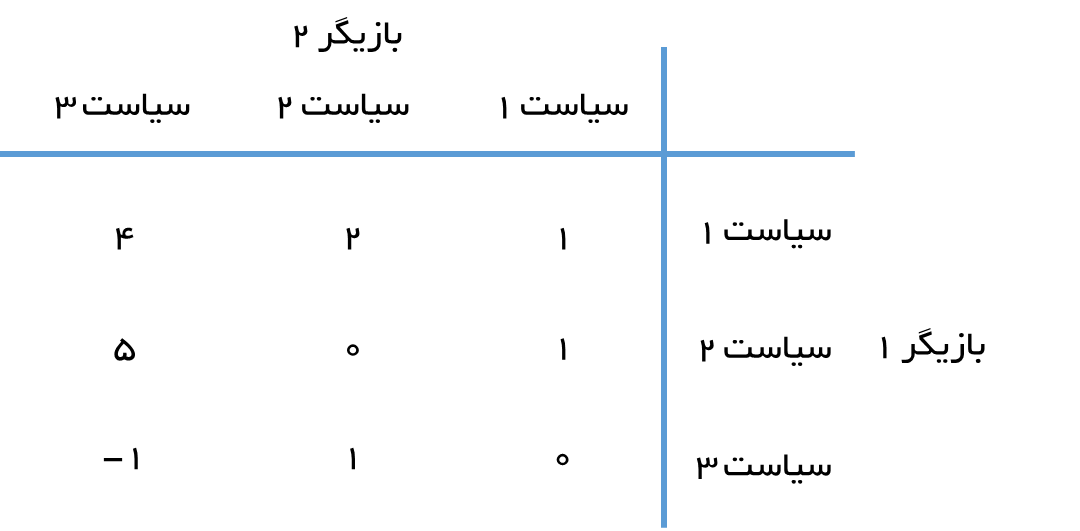
فرض کنید جدول بازده دو سیاست مدار به صورت جدول زیر است.

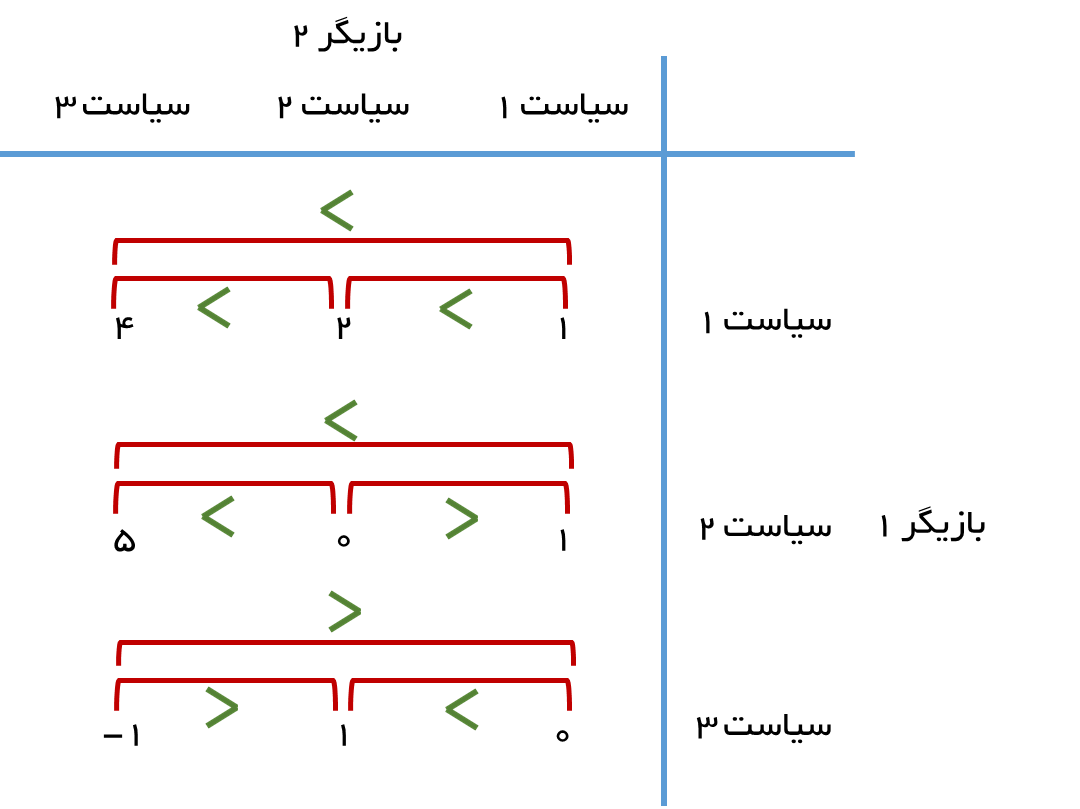
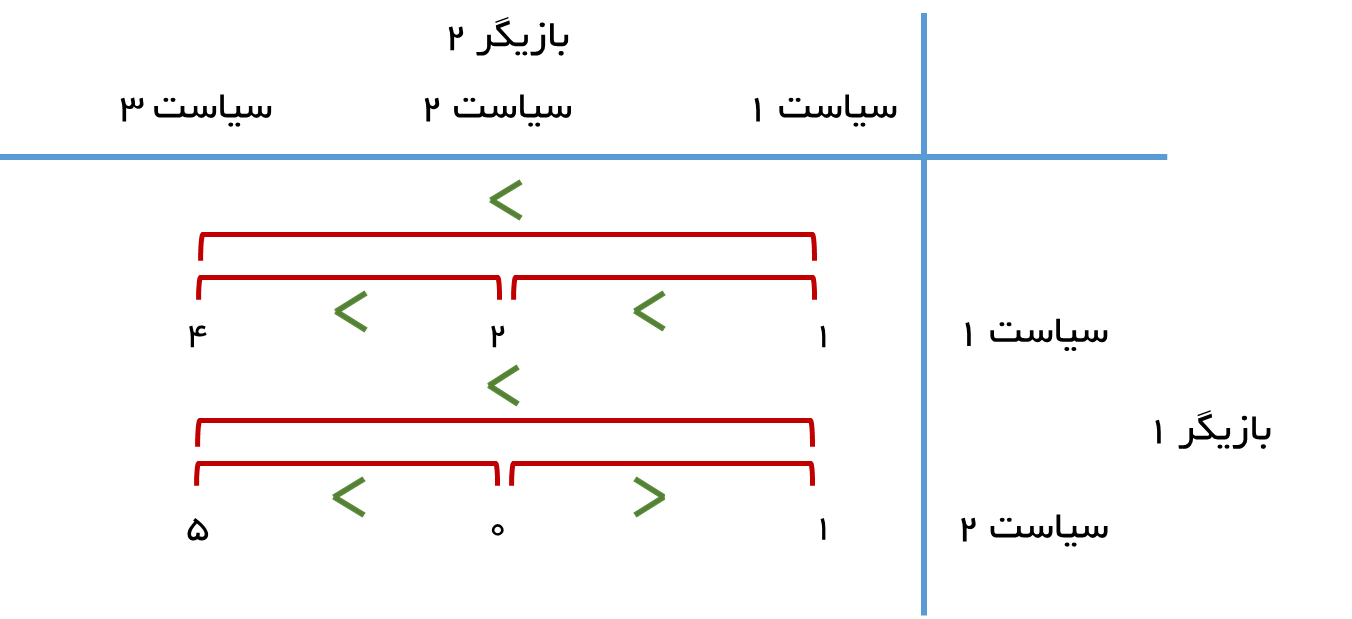
در جدول فوق، بازیگر دوم هیچ سیاستی ندرد که مشخصا بدتر از سیاست دیگر باد. در شکل زیر این وضعیت توضیح داده شده است.

توجه: برای بازیگر 2، هر چه مقدار کمتر باشد، بهتر است.

اما برای بازیگر اول، سیاست 1 بر سیاست 3 غالب است و صرف نظر از تصمیم بازیگر 2 همواره سیاست 1 بهتر از سیاست 3 است. در شکل زیر این مفهوم نشان داده شده است.

در این حالت، سیاست 3، سیاست مغلوب یا Dominated Strategy است و در هر مرحله سیاست مغلوب حذف می شود. به طور مشخص در هر مرحله سیاستی که از دیگر سیاست بدتر باشد می توان آن را کنار گذاشت. در این صورت جدول بازده به صورت زیر می شود.

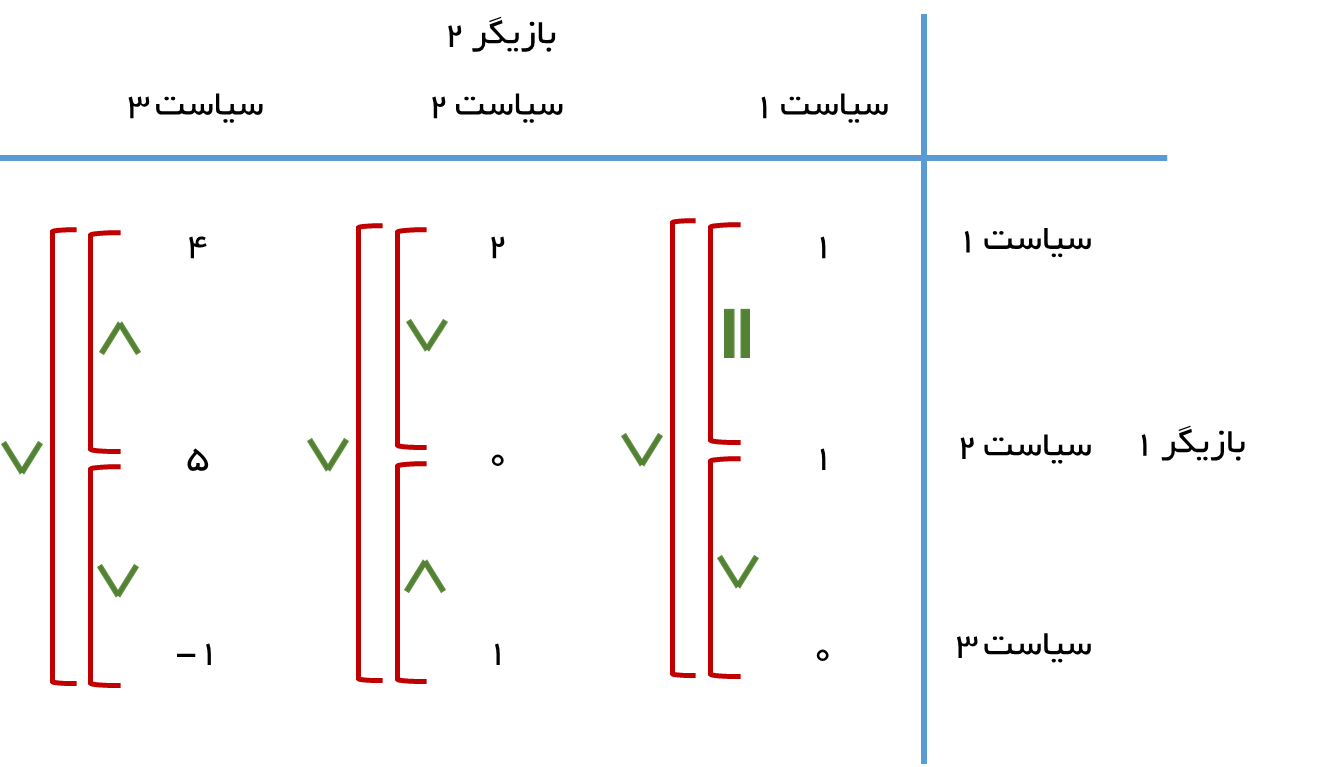
با توجه به این که هر دو بازیگر منطقی هستند، لذا بازیگر 2 می داند که بازیگر 1 فقط دو سیاست 1 و 2 را انتخاب می کند و سیاست 3 را دیگر انتخاب نمی کند. در این جدول بازیگر دوم یک سیاست مغلوب دارد که سیاست 3 است. در شکل زیر دلیل مغلوب بودن سیاست 3 نشان داده شده است.

توجه: برای بازیگر 2 هر چه مقدار بازده کمتر باشد، بهتر است.

با حذف سیاست مغلوب 3، به جدول زیر می رسیم.

در این جدول برای بازیگر اول، سیاست 1 بر سیاست 2 غالب است و سیاست 2، سیاست مغلوب برای بازیگر 1 است. که در این صورت جدول بازده به صورت زیر می شود.

همچنین برای بازیگر 2، سیاست 2 نسبت به سیاست 1، سیاست مغلوب است و ناگزیر هر دو بازیگر سیاست 1 را انتخاب می کنند.

بدین ترتیب، بازیگر اول همواره یک واحد از بازیگر دوم می برد و در این حالت ارزش بازی یا Value of the Game مساوی یک است. در صورتی که ارزش بازی برابر با صفر باشد، بازی عادلانه یا Fair Game نامیده می شود.

گونه دوم:

در این حالت فرض کنید بازده جدول به صورت زیر باشد.

در جدول فوق، سیاست مغلوبی وجود ندارد و دیگر امکان یافتن سیاست توسط حالت قبلی نیست. بازیگر اول با انتخاب سیاست 1 می تواند از 6 واحد برد تا 3 واحد باخت داشته باشد. چون بازیگر 2 منطقی است لذا سیاست 1 را انتخاب می کند تا بازیگر 1 ببازد. همچنین بازیگر 1 با انتخاب سیاست 3 می توان 5 واحد برد داشته باشد ولی بازیگر 2 این مجال را بازیگر 1 نمی دهد و 4 واحد باخت به او تحمیل می کند. همچنین با انتخاب سیاست 2، بازیگر 1 باختی را تجربه نخواهد کرد و به نظر سیاست خوبی باشد.

با تحلیل مشابه برای بازیگر 2 می توان به این نتیجه رسید که با انتخاب سیاست های 1،2، و 3 به ترتیب باختی برابر با 5 ، 0 و 6 به بار می آید و به نظر می رسد که سیاست 2 انتخاب عاقلانه ای است زیرا باخت کمتری دارد. لذا سیاست 2 برای هر دو بازیگر، سیاست مناسب است.

توجه: به طور مشخص هر بازیگر باید طوری بازی کند که حداکثر باخت خود را حداقل کند. ضابطه حداقل کردن حداکثر یا Minimax Criterion معیار اساسی نظریه بازی در انتخاب سیاست است. این ضابطه به معنی آن است که بازیگر اول باید سیاستی که حداقل بازده آن از همه بزرگتر و بازیگر دوم سیاستی که حداکثر بازده ان از همه کوچکتر باشد را انتخاب کند.

تعریف: اگر در یک بازی دو نفره مجموع صفر داشته باشیم:

(V=Max_i(Min_j a_ij)=Min_j(Max_i a_ij

آنگاه این بازی دارای نقطه زین اسبی (Saddle Point) دارد. در این صورت بهترین سیاست بازیگر 1 انتخاب (Max_i(Min_j a_ij و بهترین سیاست بازیگر 2 انتخاب سیاستی است که بازده برابر با (Min_j(Max_i a_ij باشد. به این سیاست، سیاست خالص یا Pure Strategy گفته می شود و مقدار V را ارزش بازی می نامند. در صورتی که ارزش بازی برابر صفر باشد به این بازی، بازی عادلانه یا Fair Game می گویند.

در این بازی، وجود نقطه زین اسبی نقش تعیین کننده ای دارد و باعث می شود که هیچ بازیگری نتواند از سیاست حریف به نفع خود استفاده کنند. یعنی هر گاه بازیگر دوم حدس بزند یا مطلع شود که قرار است بازیگر 1 سیاست 2 را انتخاب کند، او با تغییر سیاستی غیر از 2 تنها ضرر خود را افزایش می دهد و بنابراین هیچ یک انگیزه ای برای بررسی تغییر سیاست نخواهند داشت. به عبارت دیگر نقطه زینی در واقع برای بازی نقطه تعادل یا Equilibrium Point است. نقطه تعادل نقطه ای است که هیچ یک از بازیکنان از تغییر یک جانبه سیاست خود سودی نخواهد برد.

گونه سوم:

در این حالت فرض کنید بازده جدول به صورت زیر باشد.

اگر هر دو بازیگر مثل حالت قبلی از ضابطه حداقل حداکثر پیروی کنند چه می شود.

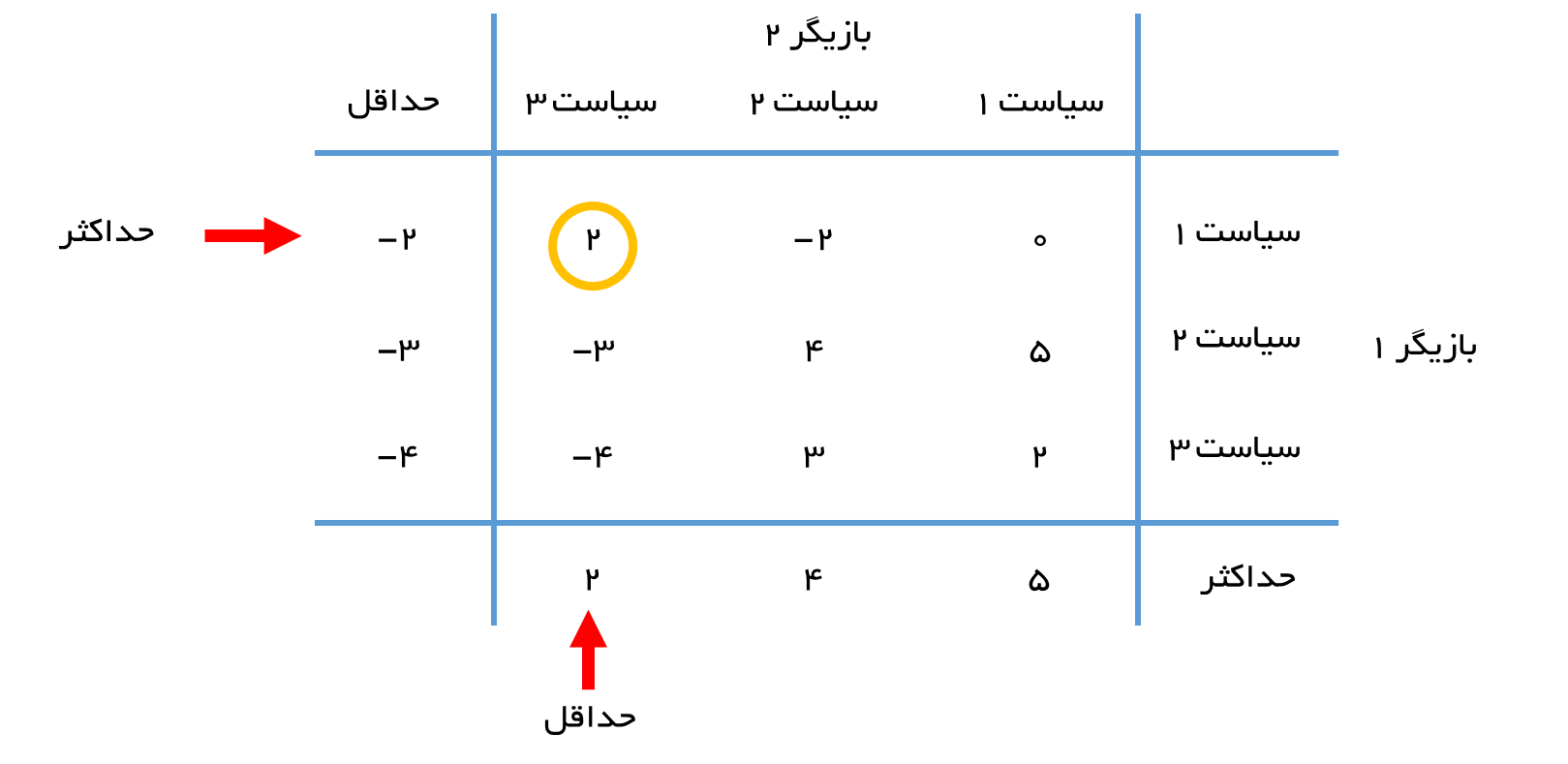
در صورتی که مشابه گونه 2 بازیگران از ضابطه حداقل حداکثر پیروی نماید. بازیگر اول می داند که کمترین مقدار بازی مساوی 2- است که حداکثر ستون حداقل یا Min است. بازیگر 1 با انتخاب سیاست1، بیش از 2 واحد نخواهد باخت. به همین ترتیب، چون بیشترین مقدار بازی برابر 2 است و بازیگر 2 می تواند مطمئن باشد که با انتخاب سیاست 3، بیشتر از 2 واحد نبازد.

چون مقدار ارزش بازی بزرگتر از صفر است لذا این بازی نقطه زین اسبی ندارد. حال ببینیم وقتی بازیگر 1، سیاست 1 و بازیگر 2 سیاست 3 را انتخاب کند چه اتفاقی می افتد. بازیگر 1 با انتخاب سیاست 1، 2 واحد می برد و در این حالت بازیگر 2، 2 واحد می بازد. برای این که بازیگر 2 از این باخت جلوگیری کند، سیاست 2 را انتخاب می کند و به جای 2 واحد باخت، 2 واحد خواهد برد. بازیگر اول هم منطقی است و برای افزایش بازده خود، سیاست 2 را انتخاب می کند و بازده خود را از 2- به 4 می رساند. با درک این موضوع، بازیگر 2 سیاست 3 را انتخاب می کند که 4 واحد باخت را با 3 واحد برد عوض می کند. باخت 3 واحدی بازیگر 1 سبب می شود که این بازیگر باخت 3 واحد را به برد 2 واحد عضو کند و لذا این حرکت از نو ایجاد می شود. در واقع جواب به صورت سیاست 1 برای بازیگر 1 و سیاست 3 برای بازیگر 2 است که جوابی ناپایدار (Unstable) است.