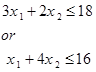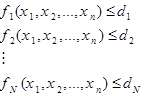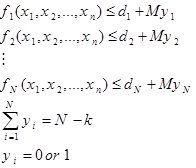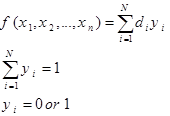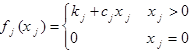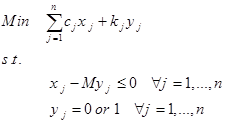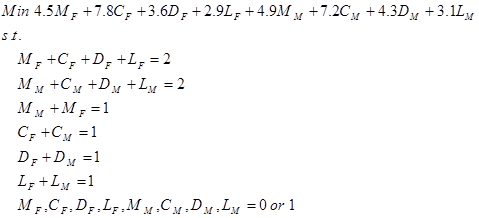مدل سازی برنامه ریزی عدد صحیح

درس 11: مدل سازی برنامه ریزی عدد صحیح

تهیه شده توسط گروه بهینه یاب

در برنامه ریزی خطی فرض بخش پذیری باعث می‌شود که در بسیاری از مسائل واقعی، چنانچه مقادیری غیر از عدد صحیح به متغیرهای صحیح داده شده که از نظر مفهومی ‌بی معنا باشد. به عنوان مثال، تعداد نفرات یا تعداد دستگاه‌ها که باید به مقادیر صحیح اختصاص یابد. در ادبیات تحقیق در عملیات بررسی موارد فوق را برنامه ریزی خطی عدد صحیح می‌نامند که به اختصار برنامه ریزی عدد صحیح نامیده می‌شود. اگر همه متغیرهای تصمیم یک مسئله برنامه ریزی خطی، عدد صحیح باشند، به آن برنامه ریزی عدد صحیح خالص ( Pure integer programming) گفته می‌شود. اگر فقط در مورد تعدادی از متغیرها فرض عدد صحیح بودن صادق باشد، به آن برنامه‌ریزی عدد صحیح مختلط (Mixed integer programming) گفته می‌شود. در ادامه یک نمونه مسئله برنامه‌ریزی صفر و یک ارایه می‌شود.

مثال: یک شرکت تولیدی تصمیم دارد به منظور توسعه فعالیت‌های خود، کارخانه جدیدی در یکی از دو شهر (الف) و (ب) ایجاد نماید. در شهری که برای این منظور انتخاب می‌شود می‌تواند انبار جدیدی هم احداث نمود ولی حداکثر یک انبار می‌تواند داشته باشد. در ستون 4 جدول زیر، ارزش خالص فعلی هر کدام از این انتخاب‌ها و در ستون آخر، سرمایه مورد نیاز آورده شده است. حداکثر بودجه برای این توسعه 24 میلیون دلار است و هدف مسئله، تعیین ترکیبی از انتخاب‌ها است که ارزش خالص را بیشینه نماید. مدل سازی برنامه ریزی عدد صحیح این مثال را انجام دهید.

حل:

متغیر تصمیم این مسئله به صورت زیر است:

به دلیل اینکه تصمیم‌های x₁ و x₂ از نوع ناسازگار هستند (شرکت فقط یک کارخانه می‌تواند بسازد)، لذا به محدودیت زیر نیاز است:

به طور مشابه برای تصمیم‌های x₃ و x₄ هم این ناسازگاری برقرار است(شرکت حداکثر یک انبار می‌تواند داشته باشد)

تصمیم‌های x₃ و x₄ تصمیم‌های وابسته به x₁ و x₂ هستند(ساختن انبار در یک شهر منوط به ساخت کارخانه است). این شرط با استفاده از محدودیت زیر بیان می‌شود:

در محدودیت اول، اگر x₁ برابر با صفر باشد (یعنی در شهر 1 کارخانه ساخته شود)، آنگاه x₂ خواهد بود. ولی اگر در شهر 1 کارخانه‌ای ساخته شود، می‌توان در این شهر انبار ساخته شود( x₃=0 or 1 ).

بنابراین شکل کلی مدل به صورت زیر است:

فرموله کردن مسائل با استفاده از متغیرهای صفر و یک

محدودیت‌های این یا آن (either-or constraint)

حالتی را در نظر بگیرید که از بین دو محدودیت موجود می‌توان یکی را انتخاب کرد ولی لزومی ندارد که هر دو محدودیت برقرار باشد. فرض کنید که در مسئله‌ای، یکی از دو محدودیت زیر باید برقرار باشد:

با استفاده از عدد M بزرگ می‌توان مدل سازی برنامه ریزی عدد صحیح این محدودیت‌ها را به صورت زیر در آورد:

که y متغیر صفر و یک است. اگر y=1 باشد، لذا خواهیم داشت:

که در این صورت محدودیت دوم برقرار است و لزومی به برقراری محدودیت اول نیست.

اگر y=0 باشد، محدودیت‌ها به صورت زیر می‌شوند:

که در این صورت محدودیت اول برقرار است و لزومی ‌به برقراری محدودیت دوم نیست.

k محدودیت از بین N محدودیت باید برقرار باشد.

اکنون حالتی را در نظر بگیرید که محدودیت‌هایی به صورت زیر وجود دارد.

می‌خواهیم k محدودیت از N محدودیت بالا برقرار باشد. مدل سازی برنامه ریزی عدد صحیح این مسئله به صورت زیر است:

توابع با N مقدار محتمل

تابع (f(x₁,x₂,…,x_nرا در نظر بگیرید که تا یکی از N مقدار d₁,d₂,…,d_N را می‌تواند اخذ نماید. مدل سازی برنامه ریزی عدد صحیح معادل زیر می شود:

مسئله هزینه ثابت

عملیات تولید، معمولا مستلزم صرف هزینه ثابت (Fixed charge) با هزینه راه اندازی (set up cost) است. در این صورت کل هزینه تولید شامل هزینه متغیر (متناسب با حجم فعالیت) و هزینه ثابت ( برای راه اندازی آن) است. اگر x_j معرف حجم فعالیت شماره j، و k_j هزینه راه اندازی آن و c_j معرف هزینه انجام هر واحد از این فعالیت باشد، هزینه کل برابر خواهد بود با:

اکنون مدل زیر را در نظر بگیرید:

مدل سازی برنامه ریزی عدد صحیح به صورت زیر می شود.

در مدل فوق، اگر y_j=0 باشد، آنگاه 0=x_j و سپس f_j=0 خواهد بود. اگر y_j=1 باشد، آنگاه x_j می‌تواند هر مقدار مثبتی اخذ نماید و خواهیم داشت:

برنامه ریزی انبار

در مدل‌سازی سیستم‌های توزیع، بایستی در باره ارزش بین هزینه‌های حمل و نقل و هزینه‌های انبارداری تصمیم‌گیری شود. فرض کنید به عنوان مثال مدیری بایستی تصمیم بگیرید از میان n انبار کدام ها را برای برآوردن تقاضای m مشتری استفاده کند. متغیر تصمیم چنین تصمیمی ‌به صورت زیر است:

x_ij: مقدار کالایی که از انبار i به مشتری j می رود.

هزینه‌های مربوطه عبارتند از:

f_i : هزینه ثابت اجاره برای انبار i اگر باز باشد

c_ij : هزینه عملیاتی در انبار i به علاوه هزینه حمل از انبار i به مشتری j

در این مسئله دو محدودیت وجود دارد که عبارتند از:

1 – تقاضا d_j برای هر مشتری بایستی از انبارها تامین شود.

2 – کالا از یک انبار تنها وقتی حمل می‌شود که انبار باز باشد.

مدل برنامه‌ریزی خطی عدد صحیح به صورت زیر می‌شود:

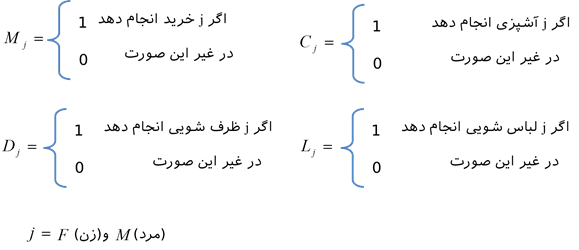
تمرین: یک زن و شوهر جوان می‌خواهند کارهای خانه (خرید، آشپزی، ظرف شویی، لباس شویی) را بین خود طوری قسمت کنند که به هر کدام از دو کار تخصیص یابد و مجموع زمانی که صرف انجام کارها می‌شود، حداقل گردد. کارایی آن‌ها در انجام این وظایف متفاوت است. زمانی که هرکدام از آن‌ها برای هر وظیفه صرف می‌کنند به شرح زیر است:

مدل سازی برنامه ریزی عدد صحیح این مثال را انجام دهید.

حل:

متغیرهای تصمیم‌گیری به صورت زیر تعریف می‌شود: