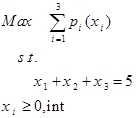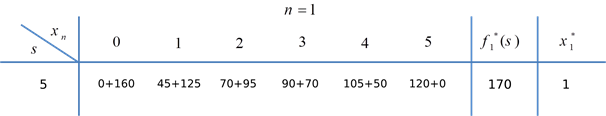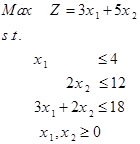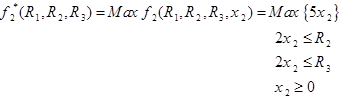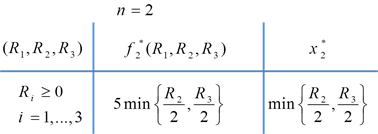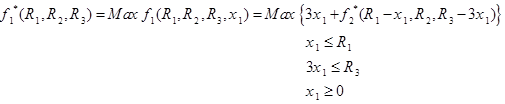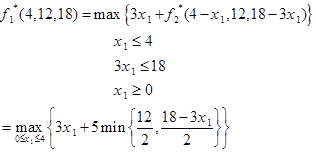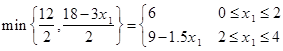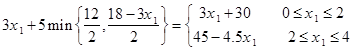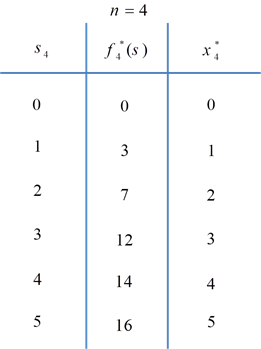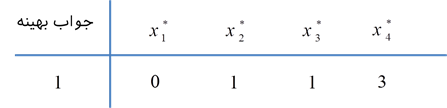برنامه ریزی پویای قطعی
برای دانلود خلاصه آموزش برنامه ریزی پویای قطعی لطفا ایمیل خود را وارد کنید تا این آموزش برای شما ارسال شود. این آموزش شامل فیلم، جزوه، پادکست و فایل ارایه است.
درس 9: برنامه ریزی پویای قطعی
تهیه شده توسط گروه بهینه یاب
برنامه ریزی پویای قطعی که ماهیتا روشی ریاضی است معمولا در رشتههایی از تصمیم گیری که مرتبط به هم هستند، کارایی دارند. برخلاف برنامه ریزی خطی، چارچوب استانداردی برای فرموله کردن برنامه ریزی پویا وجود ندارد. در واقع روش برنامه ریزی پویای قطعی ارایه روش برخورد کلی با مسئله را بیان میکند و برای هر مسئله با شرایط آن باید روش برنامه ریزی پویا را تطبیق داد.
ویژگی های مسائل برنامه ریزی پویا به شرح ذیل است:
1- مسئله را میتوان به چند مرحله (Stage) تقسیم کرد. در هر مرحله یک تصمیم اتخاذ میگردد.
2- هر مرحله به تعدادی حالت (State) وابسته است. تعداد حالات میتواند متناهی یا نامتناهی باشد.
3- در هر مرحله با اتخاذ یک تصمیم، حالت مرحله فعلی به حالتی که وابسته به مرحله بعدی باشد انتقال مییابد.
4- با فرض معلوم بودن حالت در یک مرحله، سیاست بهینه در مورد مراحل باقی مانده، مستقل از سیاستی است که در مراحل قبلی اتخاذ شده است.
5- داشتن حالت فعلی سیستم، حاوی کلیه اطلاعاتی است که برای تعیین سیاست بهینه مربوط به مراحل باقی مانده مورد نیاز است.
6- روش حل این مسائل، با پیدا کردن جواب بهینه مربوط به کلیه حالت های مرحله آخر آغاز میشود.
7- سیاست بهینه همه حالات های مرحله n را میتوان با یک رابطه برگشتی و با فرض معلوم بودن سیاست بهینه تمام حالت های مرحله (n+1) مشخص ساخت. رابطه برگشتی به صورت زیر است.
که در رابطه فوق، سیستم در مرحله n و حالت s است و هدف یافتن xn ای است که عبارت زیر کمینه شود:
یا
8- روش حل با حرکت پس رو (Backward) و با استفاده از رابطه برگشتی (Recursive relationship) از مرحله ای به مرحله قبل، بدست میآید.
برای تشریح روش برنامه ریزی پویای قطعی، مثال هایی حل میشود.
مثال: سازمان جهانی بهداشت به منظور بهداشت و آموزش پزشکی در کشورهای جهان سوم در نظر دارد 5 گروه پزشکی خود را به سه کشور اعزام کند. این سازمان باید مشخص کند به هر کشور چند گروه اختصاص یابد تا کارایی کل 3 کشور بیشینه شود. معیار سنجش کارایی این گروهها، افزایش طول عمر جمعیت است که بر حسب تعداد گروههای پزشکی به صورت جدول زیر است:
حل:
xn: معرف تعداد گروههای پزشکی که به کشور n-ام اختصاص یافته است.
حالت سیستم (s): تعداد گروههایی که در مراحل قبلی هنوز تخصیص نیافته اند.
(pi(xi : معیار سنجش کارایی از تخصیص گروه پزشکی به کشور i-ام است.
مدل برنامه ریزی ریاضی مسئله فوق به صورت زیر است:
با استفاده از قراردادهایی که در خصوص مسئله برنامه ریزی پویا داشتیم، (fn(s,xn به صورت زیر میشود.
با استفاده از موارد بالا میتوان روند حل را از n=3 (مرحله آخر) آغاز کرد.
در مرحله سوم که به دنبال یافتن تعداد گروههای پزشکی برای کشور 3-ام هستیم. s میتوان از 0 تا 5 (اعداد صحیح) مقدار بگیرد. اگر s=0 باشد، یعنی هیچ گروهی برای کشور 3 ام برای تخصیص باقی نمانده است و در مراحل قبل تخصیص انجام شده است، لذا در کشور 3-ام با توجه به جدول اطلاعات اولیه نمیتوان افزایش طول عمر داشت و لذا f*n برابر صفر میشود.
اگر s=1 باشد، یعنی یک گروه تخصیص نداده شده و میتواند برای کشور 3 ام تخصیص داده شود. با توجه به جدول، f*n برابر 50 میشود. برای s از 2 تا 5 این روند تکرار میشود.
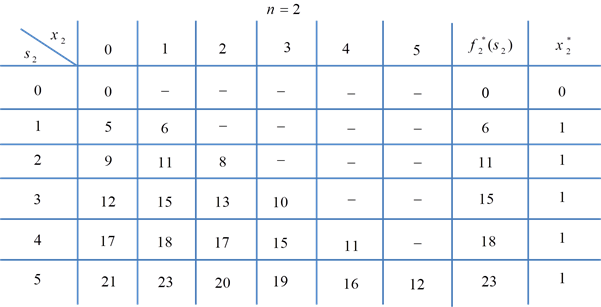
جدول برای مرحله دوم (n=2) به صورت زیر میشود:
برای تشریح نحوه محاسبه جدول فوق، چند سلول را با جزییات بیان میکنیم.
ستون x2=0
1 – در حالتی که s=0 است (یعنی تمامی گروههای پزشکی در کشور 1-ام تخصیص داده شده است) برای دو کشور 2 و 3 گروه پزشکی برای تخصیص باقی نمانده است و لذا مقدار (0)f*2 برابر صفر میشود.
2 – در حالتی که s=1 میشود، یعنی 1 گروه پزشکی امکان تخصیص دارد که برای کشور 2 و 3 تخصیص یابد. در این ستون x2=0 است، یعنی برای کشور 2-ام گروه تخصیص داده نشود و یک گروه باقی مانده است که به کشور 3-ام تخصیص مییابد. حال به جدول n=3 باز میگردیم و مقدار بهینه برای s=1 را بدست میآوریم که برابر با 50 است. لذا (f*2(x2,s برابر با 0 (افزایش عمر برای کشور 2-ام) +50 (افزایش عمر برای کشور 3-ام) میشود.
ستون x2=1
1 – همان طور که ملاحظه میشود برای s=0 ، خط تیره کشیده شده است چون اگر s=0 باشد، یعنی برای کشورهای 2 و 3 گروهی برای تخصیص باقی نمانده است و لذا تخصیص یک گروه برای کشور 2-ام ( x2=1) معنا ندارد و لذا با خط تیره (-) این نکته بیان میشود.
2 – اگر s=1 باشد، یعنی یک گروه پزشکی امکان تخصیص دارد که میتوان در کشورهای 2 و 3 (همان مراحل 2 و 3) تخصیص یابد. چون x2=1 است، این گروه به کشور 2-ام تخصیص مییابد و با توجه به جدول اولیه، افزایش طول عمرا برابر 20 سال خواهد بود. چون تخصیص 1 گروه پزشکی در کشور 2-ام، برای کشور 3-ام گروهی باقی نمیماند، لذا افزایش طول عمر برای کشور 3-ام برابر صفر است، بنابراین (f2(x2,s برابر 0+20 میشود.
3 – اگر s=2 باشد، یعنی 2 گروه پزشکی میتواند در کشورهای 2 و 3 تخصیص یابد و چون x2=1 است، یک گروه در کشور 2-ام و یک گروه باقی مانده در کشور سوم باید تخصیص یابد که در این صورت (f2(x2,s برابر 20(افزایش طول عمر با تخصیص یک گروه در کشور 2-ام) + 50 (افزایش طول عمر با تخصیص یک گروه در کشور 3-ام) میشود.
ستون (f*2(s برابر بیشترین (f2(x2,s به ازای تمامی x2 است و x2 متناظر با مقادیر بیشتر در x*2 قرار میگیرد.
در جدول مرحله آخر ( n=1 )، چون هیچ تخصیصی صورت گرفته نشده است، لذا 5 گروه پزشکی باقی مانده است که میتوان به گروههای 1، 2 و 3 تخصیص یابد. اگر xn=0 باشد یعنی در کشور 1-ام هیچ گروه پزشکی تخصیص داده نشود و 5 گروه باقی مانده برای دو کشور 2 و 3 استفاده شود که در این صورت مقدار بهینه برابر 160 میشود. نحوه محاسبه سایر مقادیر مشابه جدول n=2 است. تخصیص گروههای پزشکی به صورتx1=1,x2=3,x3=1 میشود که باعث 170 سال افزایش عمر خواهد شد.
تمرین: برنامهریزی خطی زیر را از روش برنامهریزی پویا حل کنید.
حل:
n برابر 2 و تعداد متغیرهای تصمیم گیری است.
(R1,R2,R3) بردار حالت است که Ri مقدار باقی مانده از منبع i است.
xi مقدار متغیر i-ام است.
برای مرحله دوم n=2 داریم:
مقدار تابع (f2(R1,R2,R3,x2 برابر 5x2 است که مقدارهای x2 باید محدودیت های زیر را برآورده کند.
لذا برای محاسبه x*2 مدل زیر را باید حل کرد.
جواب بهینه مدل فوق به صورت زیر است:
برای مرحله اول n=1 داریم:
چون در مرحله اول از منابع استفاده نشده است، لذا R1=4 و R2=12 و R3=18 است. لذا f*1 به صورت زیر میشود.
توجه داشته باشید که
با جایگزینی دو عبارت فوق در هم داریم:
با توجه به این که x1=2 در هر دو عبارت 3x1+30 و 45+4.5x1– بیشینه میشود، لذا x*1=2 میشود و خواهیم داشت: (2,12,12)=(R1,R2,R3) و x*2=6 و سود کل برابر با 36 خواهد شد.
تمرین: مسئول منطقه یک حزب سیاسی مشغول برنامه ریزی تبلیغاتی انتخاباتی است. برای این منظور میتواند از خدمات 5 نفر استفاده کند تا در 4 حوزه فعالیت کنند. با توجه به این که اگر یک دستیار در بیش از یک حوزه فعالیت کند، بازدهی وی کاهش پیدا میکند، لذا هر دستیار به یک حوزه گماشته میشود. همچنین حوزههای میتواند بدون دستیار بماند. برآورد میشود که افزایش تعداد آرا کاندیدا در هر حوزه با توجه به دستیارانی که برای حوزه گماشته شده است، به شرح جدول زیر است:
حل:
xn : تعداد دستیاران فعال در حوزه n-ام
(pn(xn : تعداد آرا وقتی دستیار گماشته میشود.
sn: تعداد دستیاران گماشته نشده تا مرحله n-ام.
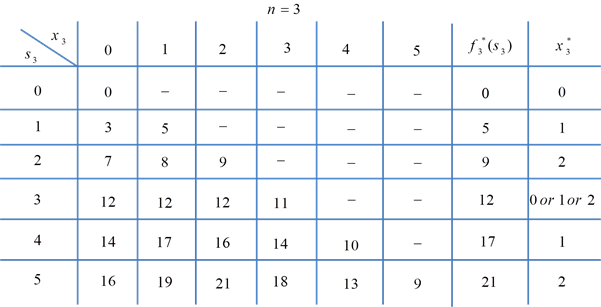
تعداد حالات برابر 4 فرض میشود:
1 – اگر s3=1 و x3=0 باشد، در این صورت برای حوزههای 3 و 4 تنها یک دستیار باقی مانده است که به حوزه 3 تعلق نمیگیرد و تنها به حوزه 4 داده میشود و تعداد آرا برابر با 0+3=3 میشود.
2 – اگر s3=2 و x3=1 باشد، در این صورت برای حوزههای 3 و 4 دو دستیار باقی مانده است که به حوزه 3 یک نفر تخصیص مییابد و یک نفر به حوزه 4 تخصیص مییابد که در این صورت تعداد آرا برابر با 3+5=8 میشود.
3 – اگر s3=3 و x3=3 باشد، در این صورت سه نفر برای تخصیص به حوزههای 3 و 4 باقی مانده است که هر سه نفر به حوزه 3 تخصیص مییابد و به حوزه 4 فردی تخصیص داده نمیشود و لذا مقدار کل آرا برابر با 11+0=11 میشود.
4 – اگر s3=5 و x3=2 باشد، در این صورت 5 نفر برای تخصیص به حوزههای 3 و 4 باقی مانده است که 2 نفر به حوزه 3 و 3 نفر به حوزه 4 تخصیص داده میشود، لذا تعداد آرا برابر با 9+12=21 میشود.
براساس جداول بالا، جواب بهینه به صورت زیر میشود: