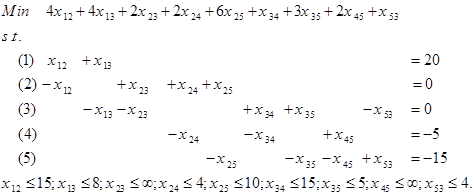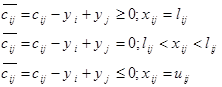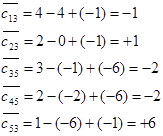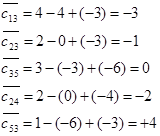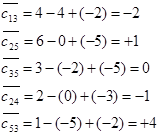مسئله جریان در شبکه با کمترین هزینه

درس 8: مسئله جریان در شبکه با کمترین هزینه

تهیه شده توسط گروه بهینه یاب

تا کنون به بررسی مسئله برنامه ریزی خطی به صورت کلی پرداختیم. در این بخش به بررسی انواع خاص مسئله برنامه ریزی خطی خواهیم پرداخت. در این بخش ابتدا به بررسی مدل عمومی جریان در شبکه پرداختیم و سپس به ارایه دستور حل سیمپلکس برای یافتن جواب بهینه خواهیم پرداخت.

مسئله عمومی جریان در شبکه

در مسئله جریان در شبکه، به دنبال توزیع محصول همگن از کارخانه (مبادی) به بازار فروش (مقاصد) هستیم. فرض کنید تعداد کل واحدهای محصول تولید شده در هر کارخانه و تعداد کل محصول مورد نیاز معلوم است. همچنین لازم نیست که محصول مستقیما به مقاصد ارسال شود بلکه امکان دارد که از طریق سایر نقاط به مراکز توزیع ارسال شود. به علاوه، قیدهای ظرفیت بعضی از خطوط حمل‌ونقل را محدود می‌کند. هدف در این مسئله کمینه کردن هزینه حمل محصول‌ها است.

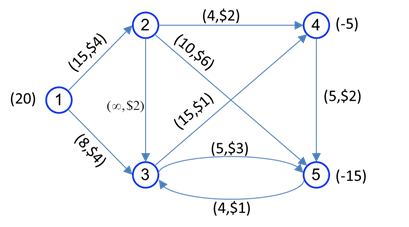
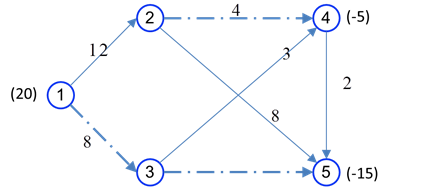
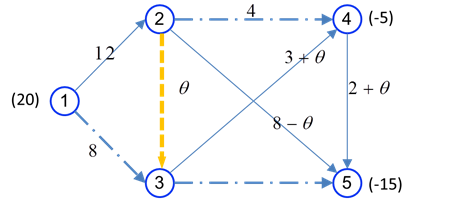
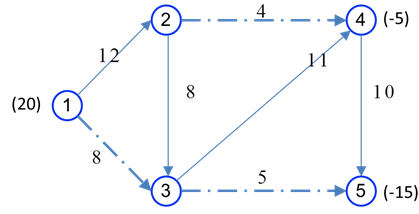
مثال عددی از مسئله جریان در شبکه در شکل زیر را در نظر بگیرید. گره‌ها با دایره های شماره دار و کمان‌ها با کمان‌ها نشان داده شده اند. کمان‌ها جهت دار هستند. مثلا مواد می‌توانند از گره 1 به گره 2 فرستاده شود ولی از گره 2 به گره 1 این امکان وجود ندارد. کمان از گره i به گره j را به صورت i-j نشان می‌دهیم.

در شکل فوق، به هر کمان یک ظرفیت و هزینه بر واحد مربوط به حمل در نظر گرفته می‌شود که در کنار هر کمان داده می‌شود. برای مثال در کمان (4-2)، جریان از 0 تا 4 واحد می‌تواند باشد و هزینه عبور هر واحد از این کمان، 2 دلار است. علامت ∞ به معنای کمان با ظرفیت نامحدود است. بالاخره، اعداد داخل پرانتز کنار گره‌ها میزان عرضه و تقاضا را نشان می‌دهد. در این شکل گره 1 مبدا و عرضه در ان برابر با 20 واحد است و گره‌ها 4 و 5 مقاصد هستند که به 5 و 15 واحد نیاز دارند که با علامت – نشان داده می‌شوند.

در مسئله جریان در شبکه، هدف یافتن الگوی جریان با هزینه کمینه است. برای تبدیل مسئله به صورت برنامه‌ریزی خطی، فرض کنید:

x_ij : تعداد واحدهای حمل شده از گره i به گره j با استفاده از کمان i-j است.

مدل برنامه‌ریزی خطی جریان در شبکه به صورت زیر ارایه می‌شود.

معادلات 1 تا 5، معادلات توازن جریان در شبکه است. برای مثال معادله جریان تعادل در گره 1 به صورت زیر می‌شود.

معادله فوق این نکته را بیان می‌کند که جریان خروجی از گره 1 ( x₁₂+x₁₃ )، باید برابر با میزان عرضه گره 1 (20) باشد. معادله توازن در گره 2، بیان می‌کند که جریان ورودی به گره 2 ( x₁₂ ) برابر جریان خروجی از گره 2 ( x₂₄+x₂₅+x₂₃) است.

مدل جریان در شبکه دارای ساختار خاصی است که برای ارایه دستور حل از آن مورد استفاده قرار می‌گیرد. متغیرهای جریان x_ij در معادلات توازن فقط ضریب 0، 1+ و 1- اخذ می‌کنند. به علاوه دقیقا در دو معادله توازن ظاهر می‌شوند: یک بار با ضریب 1+ مربوط به گره‌ای که از آن سرچشمه می‌گیرند و 1- مربوطه به گره‌ای که به آن وارد می‌شوند. با توجه به موارد فوق، فرم عمومی مسئله کمترین جریان در شبکه را به n گره به صورت زیر بیان می‌شود.

مدل فوق، مدل عمومی مسئله جریان کمینه در شبکه است. برای شرایط خاص، مدل فوق قابل تبدیل به فرم های ساده تری است که در ادامه برخی از این مدل های خاص را بیان می‌کنیم.

مسئله جریان در شبکه با کمترین هزینه

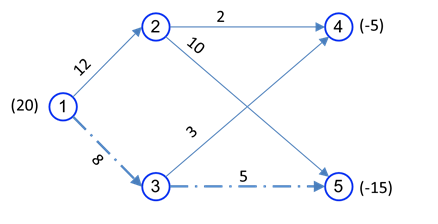
در این بخش با استفاده از مفاهیم شبکه که تا کنون بیان شده است، روش سیمپلکس شبکه ارایه می‌شود. مسئله جریان در شبکه پیچیده تر از مسئله حمل و نقل است زیرا گره‌های واسط دارد و همچنین هر کمان ظرفیت دارد. برای حل این مسئله با استفاده از روش سیمپلکس باید یک جواب امکان پذیر داشت. تعیین جواب اولیه در مسئله شبکه کمی‌ با مسئله حمل‌ونقل متفاوت است و بدست آوردن یک جواب اولیه می‌تواند نیاز به محاسبات زیادی داشته باشد. مثلا فرض کنید که جواب اولیه در دسترس است. بیان الگوریتم جریان در شبکه را در قالب یک مثال تشریح می‌کنیم.

در شکل فوق، کمان نشان دهنده متغیرهای غیراساسی (غیرپایه) هستند که در حد بالای خود قرار دارند و کمان‌های توپر، متغیرهای اساسی (پایه) هستند. کمان‌های توپر درخت گسترش را برای شبکه تشکیل می‌دهد و جواب اساسی را برای مسئله می‌سازد. برای این که تعیین شود جواب فعلی یک جواب اساسی بهینه است، باید هزینه c̄_ij همه کمان‌های غیرپایه را محاسبه کرد. برای این منظور، ابتدا مضرب‌های (y_i (i=1,2,…,n را محاسبه می‌کنیم. اگر این مضرب‌ها در روابط زیر صدق کنند:

آنگاه جواب اساسی فعلی، بهینه است. برای محاسبه مضرب‌ها ( y_i ها)، می‌توان یک مضرب را به طور دلخواه برابر صفر در نظر گرفت و مابقی مضرب‌ها را با استفاده از رابطه زیر محاسبه می شود.

براساس رابطه بالا می توان مضرب‌های ( y_i ) به صورت زیر تعیین کرد.

هزینه c̄_ij برای متغیرهای غیراساسی به صورت زیر می‌شود:

برای بهبود جواب فعلی بر اساس هزینه c̄_ij ‌های بالا دو راه حل پیش روی ماست:

1- افزایش جریان کمانی که هزینه c̄_ij منفی دارد و اکنون در کران پایین خود است.

2- کاهش متغیری که هزینه c̄_ij مثبت دارد و اکنون در کران بالای خود قرار دارد.

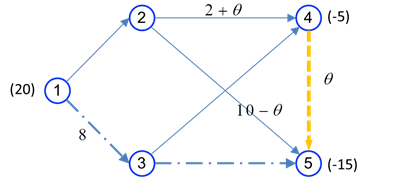
با توجه به این دو حالت، تنها کاندید، کمان (4,5) است. در شکل زیر، کمان (4,5) به شکل اضافه شد تا مشخص شود کدام کمان باید از جواب اساسی خارج شود.

مقدار θ تا 2 می‌تواند افزایش یابد که در این صورت کمان (2,4) به حد بالای خود می‌رسد و از جواب اساسی خارج می‌شود. لذا جواب اساسی فعلی به صورت زیر می‌شود.

مقدار مضرب‌های y_i با توجه به فرض y₂ = 0 می‌تواند از معادله زیر بدست آید.

براساس رابطه بالا می توان مضرب ها را به صورت زیر می‌شود.

هزینه c̄_ij برای تعیین کمان ورودی به جواب اساسی و کمان خروجی از جواب اساسی به صورت زیر است.

در این مرحله کمان (2,3) وارد جواب اساسی می‌شود. برای خروج کمان خروجی به صورت زیر عمل می‌شود.

مقدار θ تا 8 می‌تواند افزایش یابد که در این صورت کمان (2,5) از جواب اساسی خارج می‌شود. لذا جواب اساسی به صورت زیر می‌شود.

بر اساس جواب اساسی فوق، مضرب‌ها محاسبه می شود.

با توجه به مضرب‌های فوق، مقدار هزینه c̄_ij به صورت زیر می‌شود:

چون همه هزینه های c̄_ij منفی برای متغیرهای غیر پایه در کران بالا و همه هزینه‌های c̄_ij مثبت برای متغیرهای غیر پایه در کران پایین خود هستند، لذا جواب فوق، جواب بهینه است.