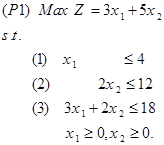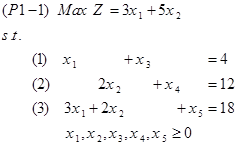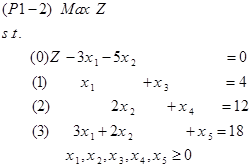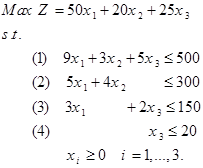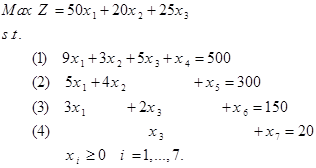درس 2: روش سیمپلکس اولیه

تهیه شده توسط گروه بهینه یاب

 

روش سیمپلکس اولیه، الگوریتمی فرایندی است که در آن یک رویه نظام گرا (systematic) آنقدر تکرار می‌گردد تا سرانجام به جواب مطلوب یا بهینه برسد. مجموعه قدم‌هایی که در چنین فرآیندی هر دفعه تجدید می‌شود را یک تکرار (Iteration) می نامند. به این‌ ترتیب، الگوریتم یک مسئله دشوار را به مجموعه از مسائل آسان‌تر جایگزین می نماید.

مقدمات روش سیمپلکس اولیه

در یک دستورالعمل جبری کار با معادلات تساوی به مراتب ساده از نامعادلات است. از این رو نخستین قدم روش سیمپلکس اولیه تبدیل محدودیت‌های کارکردی از شکل نامعادله به معادله است. محدودیت‌های نامنفی بودن را می‌توان به صورت نامعادلات باقی گذاشت زیرا به طور مستقیم در فرایند حل وارد نمی‌شوند. تبدل نامعادله به معادله با معرفی متغیرهای لنگی (slack variable) انجام می‌شود. در ادامه مدل زیر را با استفاده از سیمپلکس حل می‌کنیم تا با قسمت‌های مختلف این الگوریتم در قالب یک مثال آشنا شویم. مدل به صورت زیر است:

 

اکنون محدودیت‌های کارکردی (1) را در نظر بگیرید. متغیر لنگی این محدودیت به صورت x₃=4 – x₁ تعریف می‌شود و در واقع مقدار کمبود سمت چپ محدودیت 1 از مقدار سمت راست محدودیت 1 است، لذا می‌توان محدودیت 1 را به صورت زیر بازنویسی کرد:

معادله فوق زمانی با محدودیت 1 برابر است که x₃ ≥ 0 باشد. از این رو محدودیت 1 با مجموعه محدودیت‌های زیر معادل است:

برای روشن شدن موضوع یک مثال ساده می زنیم. محدودیت x₁ ≤ 4 را در نظر بگیرید. اگر x₁ = 1 باشد در این صورت 1 < 4 خواهد شد و مقدار متغیر لنگی این محدودیت برابر با x₃ = 3 می‌شود. در این صورت شکل معادله رابطه x₁ ≤ 4 به صورت 4 = x₃ + x₁ می‌شود که در این فرم معادله x₁ = 1 و x₃ = 3 است.

به صورت مشابه برای سایر نامعادلات می‌توان مدل (P1) را به صورت زیر بازنویسی کرد:

مدل (P1-1) کاملا معادل مدل (P1) ولی این شکل جدید برای عملیات جبری به مراتب ساده تر است. در مدل (P1-1) تعداد متغیرهای برابر 5 و تعداد معادلات برابر 3 است که در این حالت با دستگاه معادلات با دو درجه آزادی مواجه هستیم. در این صورت می‌توان در هر مرحله برای دو متغیر مقدار دلخواهی قرار داد و دستگاه سه معادله، سه مجهول را حل کرد. در روش سیمپلکس (simplex) این دو متغیر اضافی برابر صفر در نظر گرفته می‌شوند. متغیرهایی که برابر صفر در نظر گرفته می‌شوند، متغیرهای غیر اساسی (non-Basic variables) و سایر آن‌ها متغیرهای اساسی (Basic variables) نامیده می‌شوند. به جوابی که تمامی متغیرهای غیراساسی برابر صفر باشند، جواب اساسی (Basic solution) و جواب اساسی که در آن متغیرهای اساسی نامنفی هستند را جواب اساسی موجه (Basic feasible solution) می نامند.

ساده تر است که تابع هدف نیز همزمان و همردیف با سایر محدودیت‌ها برخورد شود. بنابراین، قبل از شروع ارایه روش سیمپلکس، مسئله (P1-1) را به صورت زیر بازنویسی می‌کنیم.

در مدل (P1-2) ، معادله صفر که همان تابع هدف است و جز محدودیت‌ها مدل محسوب می‌شود و چون معادله صفر به صورت تساوی است، دیگر نیاز به اضافه کردن متغیر لنگی نمی باشد.

دستور حل روش سیمپلکس اولیه

در این بخش به ارایه روش سیمپلکس اولیه می پردازیم. به صورت خلاصه،روش سیمپلکس اولیه در هر مرحله به دنبال یافتن جواب های اساسی موجه است که هر جواب از جواب قبلی بدتر نباشد تا سرانجام یک جواب اساسی موجه بهینه یافته شود. برای تبدیل از یک جواب اساسی موجه به جواب اساسی موجه دیگر، کافی است یک متغیر اساسی به متغیر غیر اساسی ( متغیر اساسی خروجی) و در مقابل یک متغیر غیراساسی به متغیر اساسی (متغیر اساسی ورودی) تبدیل شود. با این تغییرات جواب اساسی موجه فعلی به جواب اساسی موجه مجاور حرکت می کند. اگر یک جواب اساسی موجه از تمام جواب‌های اساسی موجه مجاور بهتر بود، آن جواب، جواب بهینه است و الگوریتم در این مرحله به پایان می رسد. در شکل زیر خلاصه مراحل روش سیمپلکس اولیه به صورت کلی آورده شده است.

هر یک از قسمت‌های الگوریتم سیمپلکس اولیه را در قالب یک مثال بیان می‌کنیم.

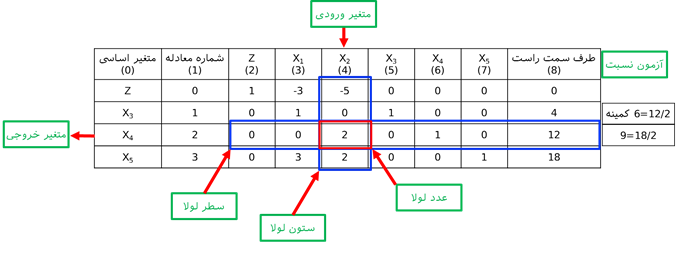
گام ابتدایی: متغیرهای لنگی (x₃ , x₄ , x₅) را متغیرهای اساسی بنامید و متغیرهای (x₁ , x₂ ) را به عنوان متغیرهای غیراساسی برابر با صفر قرار دهید. برای سادگی در انجام محاسبات، ضرایب متغیرهای و اعداد سمت راست را در جدولی به عنوان جدول سیمپلکس (Simplex Tableau) تبت می‌شود. جدول سیمپلکس مثال (P1-2) به صورت جدول زیر می‌شود.

چون هر معادله شامل یک متغیر اساسی با ضریب +1 است، لذا مقدار هر متغیر اساسی برابر با عدد ثابت سمت راست معادله خواهد بود. جواب موجه اساسی جدول فوق برابر (x₁= 0,x₂ = 0,x₃ = 4,x₄ = 12, x₅ = 18 ) است که از این به بعد به صورت ( 0,0,4,12,18 ) نمایش داده می‌شود.

گام توقف: اگر و فقط اگر تمام ضرایب معادل صفر مقادیر غیر منفی ( ≥ 0 ) باشد، آن وقت جواب اساسی موجه فعلی، جواب بهینه است و در این صورت توقف کنید. در غیر این صورت برای پیدا کردن جواب اساسی موجه مجاور به گام تکراری بروید.

گام تکراری:

زیر گام 1 – متغیری که دارای بزرگترین ضریب منفی در معادله صفر است را به عنوان متغیر اساسی ورودی انتخاب کنید. افزایش مقدار این متغیر غیراساسی منجر به تندترین آهنگ رشد مقدار تابع هدف می‌شود. مستطیلی به دور ستونی که زیر این متغیر بکشید و آن را ستون لولا (Pivot Column) بنامید. در این مثال، بزرگترین ضریب منفی (5-) بوده و مربوط به متغیر است و لذا به عنوان متغیر اساسی ورودی انتخاب می‌شود.

زیر گام 2 – متغیر اساسی خروجی به صورت زیر تعیین می‌شود:

الف) ضرایب مثبت ستون لولا را در نظر بگیرید.

ب) اعداد سمت راست را به این ضرایب تقسیم کنید.

پ) سطری را انتخاب کنید که نسبتی که برای آن در قسمت (ب) بدست آمده است، کوچکترین باشد.

ت) متغیر اساسی این معادله، متغیر اساسی خروجی است.

مستطیلی به دور این معادله بکشید و آن را سطر لولا (Pivot Row) بنامید. عددی که در هر دو مستطیلی قرار می‌گیرد را عدد لولا (Pivot Number) می نامیم.

نتایج عملیات بالا در جدول زیر آمده است.

در جدول فوق متغیر x₂ متغیر اساسی ورودی و x₄ متغیر اساسی خروجی است.

زیر گام 3 – جواب اساسی جدید را به کمک یک جدول سیمپلکس جدید بدست آورید. مراحل به دست آوردن جدول جدید به صورت زیر است.

الف) در ستون (0)، متغیر x₄ را حذف و به جای آن متغیر x₂ را قرار دهید.

ب) برای تبدیل ضریب متغیر x₂ به یک، تمام سطر لولا را بر عدد لولا تقسیم نمایید.

پ) برای اینکه متغیر اساسی x₂ از سایر معادلات حذف شود، هر سطر (شامل سطر مربوط به معادله صفر) به استثنای سطر لولا به صورت زیر تغییر نماید.

سطر جدید(به جز سطر لولا) = سطر قدیم – سطر لولای جدید × ضریب ستون لولا

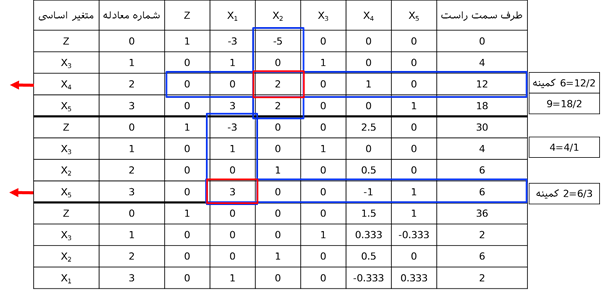
پس از ایجاد جدول سیمپلکس جدید، به گام توقف می رویم. در صورت این که شرط توقف برقرار باشد الگوریتم متوقف می‌شود و در غیر این صورت به گام تکرار می رویم. این روند تا برآورده شدن شرط توقف ادامه می‌دهیم. جدول کامل سیمپلکس برای (P2-1) به صورت زیر می‌شود.

در جدول فوق، جواب اساسی موجه (2,6,2,0,0) با Z=36 شرط توقف را برآورده می سازد و لذا این جواب بهینه است.

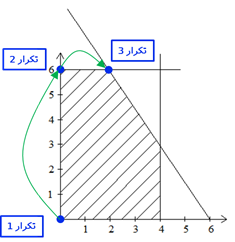
نکته: در هر گام از گام تکرار الگوریتم سیمپلکس، یکی از نقاط گوشه محدوده امکان پذیر را مورد آزمون قرار می‌دهد. با توجه به کوچکی اندازه مدل، می‌توان نمایش حرکت بر روی گوشه‌های ناحیه امکان پذیر را در نمایش هندسی مدل (P1) ملاحظه کرد که در زیر آمده است.

نکته: اگر در روش سیمپلکس به جای انتخاب بزرگترین ضریب منفی از نظر قدر مطلق را انتخاب نمی کردیم، از سمت راست به جواب بهینه نزدیک می شدیم که یک جواب اساسی موجه دیگر مورد بررسی قرار می‌گرفت.

قیمت‌های سایه (shadow prices):

روش سیمپلکس اولیه علاوه بر جواب بهینه اطلاعات با ارزش دیگری تولید می نماید. قیمت سایه منبع i (که با ^* y_i نشان داده می‌شود ) ارزش نهایی (Marginal value) این منبع را می سنجند که مبین آهنگ افزایش Z در اثر افزایش ملایم مقدار موجود این منبع ( b_i ) است. توجه شود که میزان افزایش در b_i باید به قدری کافی کوچک باشد که مجموعه متغیرهای فعلی همچنان بهینه باقی بماند زیرا به مجرد اینکه مجموعه متغیرهای اساسی تغییر کند، ارزش نهایی نیز تغییر می کند. روش سیمپلکس اولیه قیمت سایه را با ^* y_i که معرف ضریب متغیر لنگی i-ام در معادله صفر جدول نهایی سیمپلکس است، مشخص می سازد.

برای نمونه در مثال (P1)، قیمت سایه منبع 1 برابر ضریب متغیر معادله صفر (برابر با صفر)، قیمت سایه منبع 2 برابر ضریب متغیر x₄ در معادله صفر (برابر 1.5) و قیمت سایه منبع 3 برابر ضریب متغیر x₅ در معادله صفر(برابر 1) است. تعبیر دیگر قیمت سایه منبع 1 این است که حداکثر قیمتی که پرداخت آن برای افزایش یک واحد از این منبع مقرون به صرفه است. به تعبیر دیگر، حداکثر منبعی که برای افزایش یک واحد از منبع می‌توان پرداخت کرد.

تمرین: کارخانه‌ای تولید یکی از محصولات غیر سودآور خط تولید خود را متوقف ساخته است که در این صورت ظرفیت تولیدی قابل ملاحظه‌ای آزاد کرده است. از این ظرفیت ایجاد شده برای تولید سه محصول 1،2، و 3 استفاده می‌شود. ظرفیت آزاد ماشین آلات مورد نیاز این سه محصول به صورت زیر است.

میزان ماشین ساعت لازم برای تولید سه محصول به صورت زیر است:

دپارتمان فروش با مطالعه بازار به این نتیجه رسیده است که تولید محصولات 1 و 2 به هر میزان در بازار خواهان دارد ولی روش محصول 3 در هر هفته بیش از 20 واحد مسیر نیست. سود محصول‌های 1، 2، و 3 به ترتیب برابر با 50، 20، و 25 است.

الف) مدل برنامه‌ریزی خطی فوق را با هدف حداکثر کردن سود فرمول بندی کنید.

ب) مسئله را با روش سیمپلکس حل نمایید.

حل:

x_i : را تعداد محصول نوع i در هر هفته در نظر بگیرید (i=1,2,3 ).

الف) مدل برنامه‌ریزی خطی این مسئله به صورت زیر می‌شود.

 

محدودیت 1 همان محدودیت ظرفیت فرز، محدودیت 2 همان محدودیت تراش، محدودیت 3 همان محدودیت سنگ، محدودیت 4 همان محدودیت کشش بازار است.

ب) برای حل مدل فوق، ابتدا مدل را به فرم استاندارد تبدیل می‌کنیم.

 

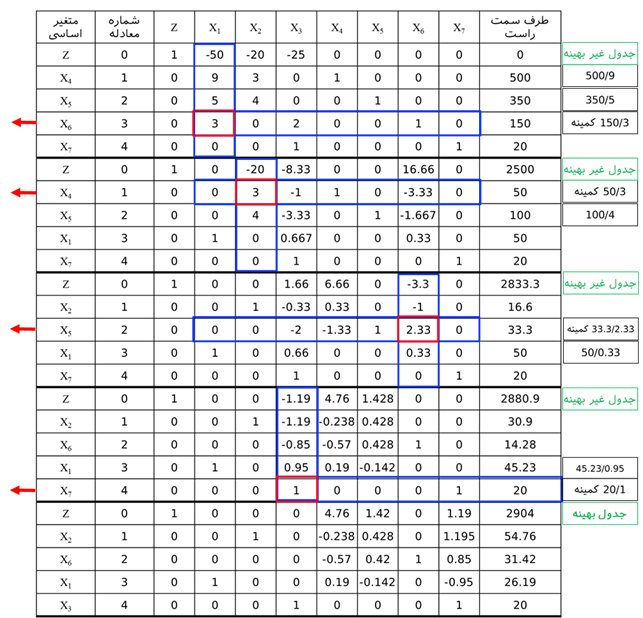
حل مدل فوق با استفاده روش سیمپلکس اولیه به صورت زیر می‌شود.

جواب بهینه به صورت ( 26.19,54.76,20 )=( x₁,x₂,x₃ ) و Z* = 2904 می‌شود. میزان کمبود و هزینه‌های سایه به صورت زیر می‌شود.