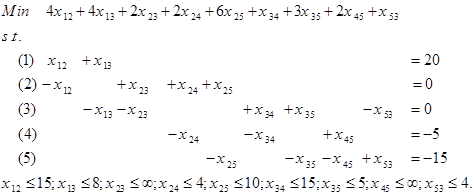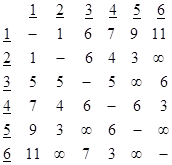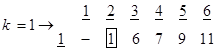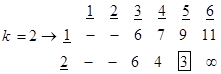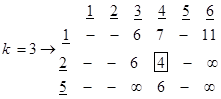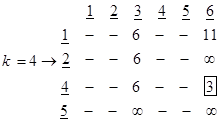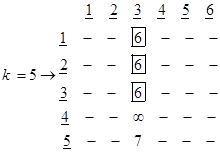برای دانلود خلاصه آموزش مسئله درخت پوشای کمینه لطفا ایمیل خود را وارد کنید تا این آموزش برای شما ارسال شود. این آموزش شامل فیلم، جزوه، پادکست و فایل ارایه است.
درس 7: مسئله درخت پوشای کمینه
تهیه شده توسط گروه بهینه یاب
تا کنون به بررسی مسئله برنامه ریزی خطی به صورت کلی پرداختیم. در این بخش به بررسی انواع خاص مسئله برنامه ریزی خطی خواهیم پرداخت. در این بخش ابتدا به بررسی مدل عمومی جریان در شبکه پرداختیم. سپس به بررسی مدل های خاص جریان در شبکه مانند مسئله حمل و نقل،مسئله درخت پوشای کمینه، مسئله جریان بیشین و مسئله کوتاه ترین مسیر خواهیم پرداخت.
مسئله عمومی جریان در شبکه
در مسئله جریان در شبکه، به دنبال توزیع محصول همگن از کارخانه (مبادی) به بازار فروش (مقاصد) هستیم. فرض کنید تعداد کل واحدهای محصول تولید شده در هر کارخانه و تعداد کل محصول مورد نیاز معلوم است. همچنین لازم نیست که محصول مستقیما به مقاصد ارسال شود بلکه امکان دارد که از طریق سایر نقاط به مراکز توزیع ارسال شود. به علاوه، قیدهای ظرفیت بعضی از خطوط حملونقل را محدود میکند. هدف در این مسئله کمینه کردن هزینه حمل محصولها است.
مثال عددی از مسئله جریان در شبکه در شکل زیر را در نظر بگیرید. گرهها با دایره های شماره دار و کمانها با کمانها نشان داده شده اند. کمانها جهت دار هستند. مثلا مواد میتوانند از گره 1 به گره 2 فرستاده شود ولی از گره 2 به گره 1 این امکان وجود ندارد. کمان از گره i به گره j را به صورت i-j نشان میدهیم.
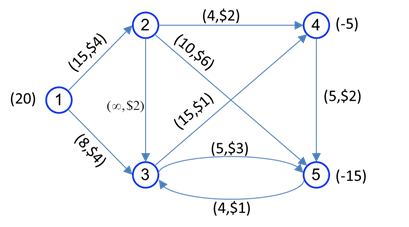
در مسئله جریان در شبکه، هدف یافتن الگوی جریان با هزینه کمینه است. برای تبدیل مسئله به صورت برنامهریزی خطی، فرض کنید:
xij : تعداد واحدهای حمل شده از گره i به گره j با استفاده از کمان i-j است.
مدل برنامهریزی خطی جریان در شبکه به صورت زیر ارایه میشود.
معادلات 1 تا 5، معادلات توازن جریان در شبکه است. برای مثال معادله جریان تعادل در گره 1 به صورت زیر میشود.
معادله فوق این نکته را بیان میکند که جریان خروجی از گره 1 ( x12+x13 )، باید برابر با میزان عرضه گره 1 (20) باشد. معادله توازن در گره 2، بیان میکند که جریان ورودی به گره 2 ( x12 ) برابر جریان خروجی از گره 2 ( x24+x25+x23) است.
مدل جریان در شبکه دارای ساختار خاصی است که برای ارایه دستور حل از آن مورد استفاده قرار میگیرد. متغیرهای جریان xij در معادلات توازن فقط ضریب 0، 1+ و 1- اخذ میکنند. به علاوه دقیقا در دو معادله توازن ظاهر میشوند: یک بار با ضریب 1+ مربوط به گرهای که از آن سرچشمه میگیرند و 1- مربوطه به گرهای که به آن وارد میشوند. با توجه به موارد فوق، فرم عمومی مسئله کمترین جریان در شبکه را به n گره به صورت زیر بیان میشود.
مدل فوق، مدل عمومی مسئله جریان کمینه در شبکه است. برای شرایط خاص، مدل فوق قابل تبدیل به فرم های ساده تری است که در ادامه برخی از این مدل های خاص را بیان میکنیم.
مسئله درخت پوشای کمینه یا درخت پوشای مینیمم Minimum spanning tree
در اینجا اتصال گرههای مختلف یک شبکه به یکدیگر مدنظر است. به طوری که کمترین فاصله در این اتصالها رعایت شود. شاخههایی که گرهها (نقاط) را به یکدیگر اتصال میدهند، بدون جهت هستند. چند نمونه کاربرد این مسئله عبارتند از:
1 – یک شرکت در احداث ساختمان مرکزی خود، در خصوص برق رسانی به نقاط گوناگون مورد نظر در آن ساختمان می خواهد کمترین میزان کابل برق را استفاده کند.
2 – وزارت راه برای برقرار اتصال بین روستاهای یک منطقه به دنبال راه کاری است که براساس آن، طول جادههای ارتباطی حداقل باشد.
3 – اداره آب و فاضلاب در نظر دارد کمترین طول لوله را برای ایجاد شبکه آبرسانی در یک شهرک در حال احداث مصرف کند.
الگوریتم درخت پوشای کمینه
با فرض اینکه به تعداد n نقطه (گره) با شماره 1 تا n در مسئله مورد نظر وجود دارد، گامهای الگوریتم چنین است:
گام 1: ماتریس مربع nxn فواصل بین نقاط 1 تا n را تشکیل دهید.
گام 2: از یک نقطه دلخواه شروع کنید و کوتاهترین فاصله بین آن نقطه تا سایر نقاط را بدست آورید. برای این منظور سطر مربوط به نقطه انتخابی را از ماتریس اصلی خارج و یک ماتریس 1xn تشکیل دهید و در این ماتریس کوچکترین عدد را برگزینید. در این صورت عدد انتخاب شده، کوتاهترین فاصله نقطه انتخابی و نقطه ای است که در ستون مربوط به عدد یادشده قرار دارد. نقطه اخیر را به عنوان نقطه در نظر بگیرید.
گام 3: در این مرحله، ماتریس 2xn مربوط به دو نقطه اشاره شده را تشکیل و کوچکترین عدد داخل ماتریس را انتخاب نمایید تا سومین نقطه نیز بدست آید. همین طور ادامه دهید تا کلیه نقاط انتخاب شوند.
گام 4: ترتیب بدست آوردن این نقاط نشان دهنده ترتیب حرکت بهینه در درخت مورد نظر است و مجموع فواصل در این درخت، حداقل فاصله ممکن برای اتصال نقاط خواهد بود.
نکته: چنانچه در مرحله ای، دو یا چند عدد مساوی در ماتریس وجود داشته باشد، دو یا چند جواب برای مسئله وجود خواهد داشت.
مثال: در یک ساختمان می بایست بین شش نقطه با فواصل مندرج در ماتریس زیر، سیم کشی برق انجام شود. علامت ∞ برای فاصله دو نقطه در ماتریس، دلالت بر عدم امکان سیم کشی بین آنها دارد. با استفاده از الگوریتم درخت پوشش کمینه، درخت حداقل سیم کشی را تعیین و حداقل مقدار سیم مصرفی را بدست آورید.
حل:
در مرحله 1 ( k =1 ) باید یک نقطه به دلخواه انتخاب شود. در این جا نقطه 1 انتخاب میشود ( هر نقطه دیگری نیز میتوانست انتخاب شود). ماتریس 1×6 مربوطه به صورت زیر تشکیل میشود:
در این ماتریس، کوچکترین عدد برابر با 1 می باشد که علامت مربع بر دور آن مشخص شده است. این عدد مربوط به فاصله بین نقطه 1 با نقطه 2 می باشد و در نتیجه کوتاهترین فاصله تا نقطه 2 بدست آمد.
در مرحله 2 ( k=2 ) نقطه 2 نیز که کوتاهترین فاصله تا آن در مرحله گذشته تعیین شده، به ماتریس 1×6 اضافه شده و ماتریس 2×6 زیر ایجاد میگردد.
توجه: چون نقاط 1 و 2 تعیین تکلیف شدند، در ماتریس بالا علامت – در ستونهای 1 و 2 درج شده، یعنی بررسی این نقاط لازم نیست. در این ماتریس کوچکترین عدد برابر با 3 و مربوط به فاصله بین نقطه 2 با نقطه 5 است و بنابراین کوتاهترین فاصله تا نقطه 5 نیز بدست آمد.
در مرحله 3 ( k=3 ) با افزایش سطر 5، ماتریس 3×6 ایجاد میگردد:
در مرحله 4، کوچکترین عدد در این ماتریس برابر با 4 و مربوط به فاصله بین نقطه 2 با نقطه 4 است و بنابراین کوتاهترین فاصله تا نقطه 4 بدست آمده است. به همین ترتیب مراحل بعدی نیز انجام میشود که ماتریسهای آنها عبارتند از:
ماتریس مرحله 5 ( k=5 ) به صورت زیر است:
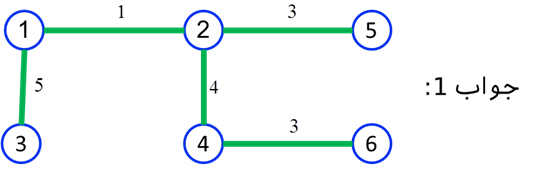
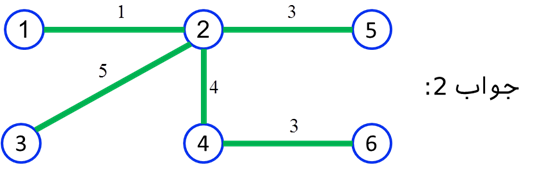
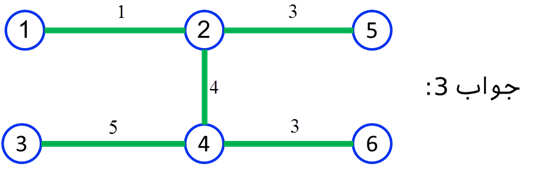
در مرحله 5 ( k=5 ) ملاحظه میشود سه عدد مساوی 6 به عنوان کوچکترین عدد در این ماتریس وجود دارند، بنابراین مسائل سه جواب دارد. یعنی برای سیم کشی برق به نقطه 3 از هر یک از نقاط 1، 2 و یا 4 میتوان اقدام نمود. چون کوتاهترین فاصله تا تمامی نقاط بدست آمد، در نتیجه الگوریتم به پایان می رسد. سه جواب مسئله (درخت پوشش کمینه) در شکل زیر آمده است.