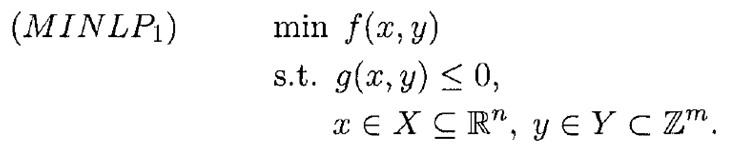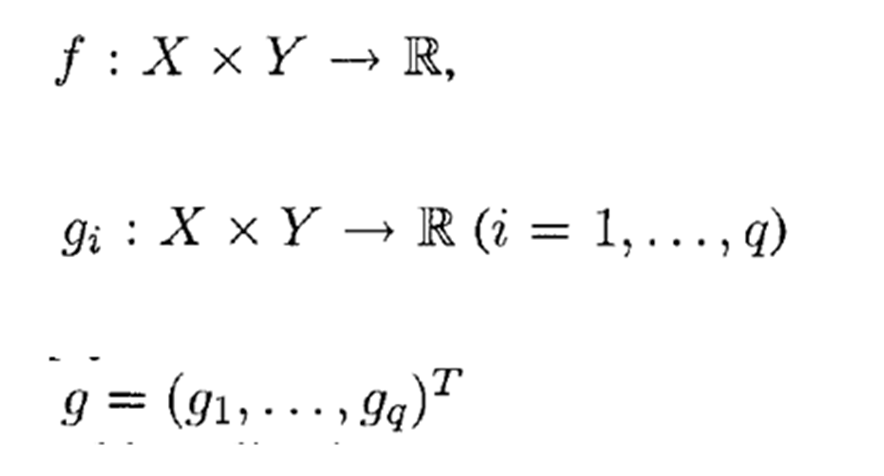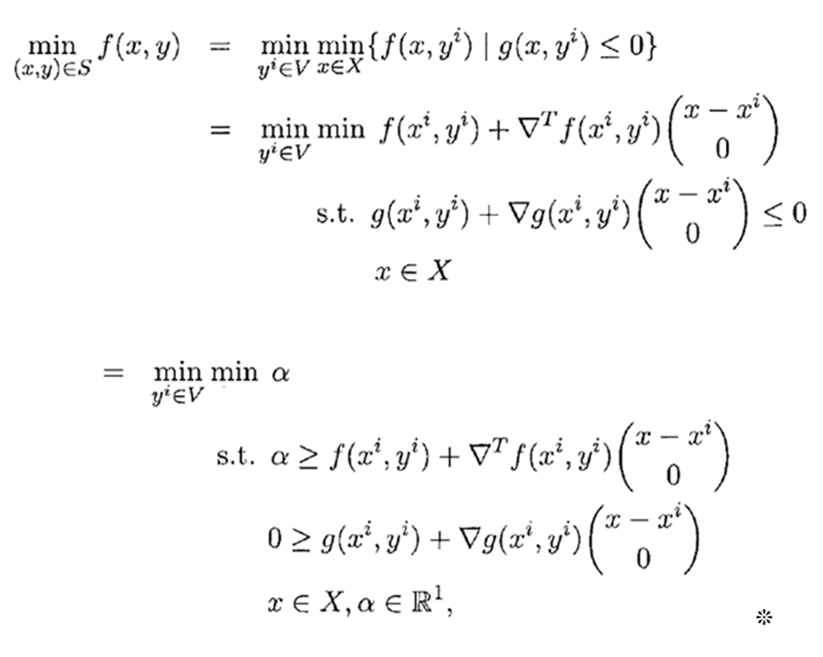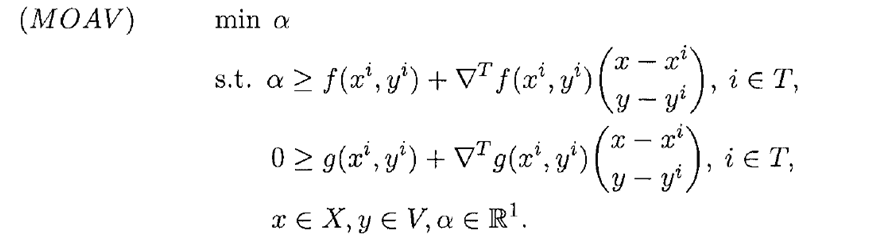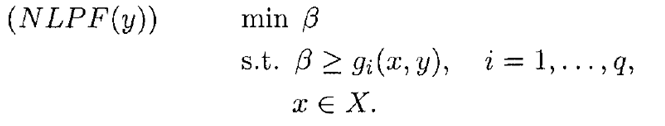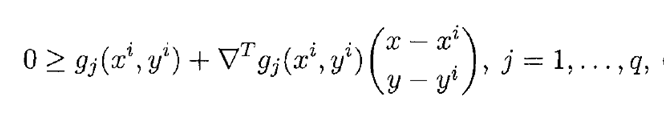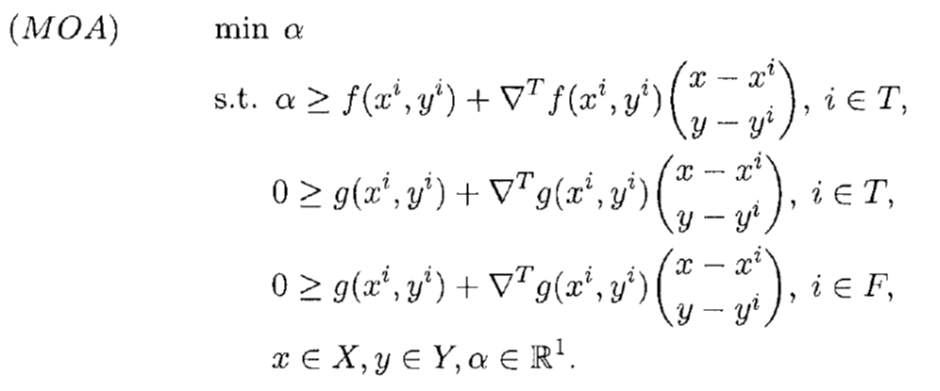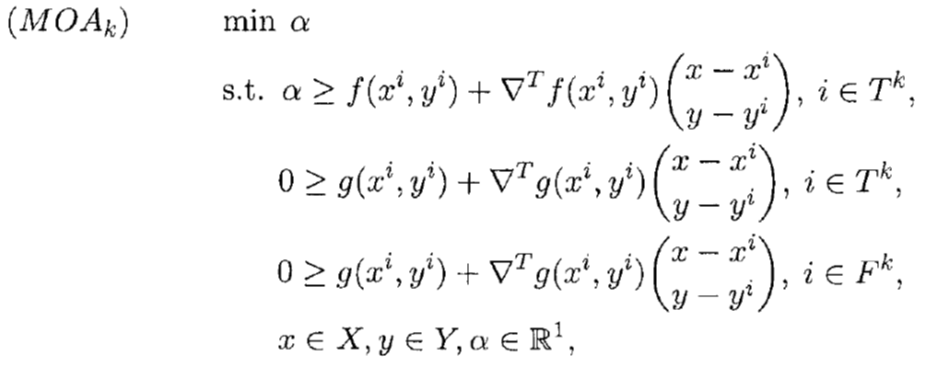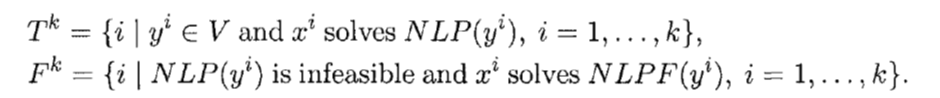درس 33: آموزش روش Outer Approximation

تهیه شده توسط گروه بهینه یاب

آ

مقدمه

روش Outer approximation، یک روش رایج برای مسائل برنامه ریزی عدد صحیح مختلط غیر خطی یا Mixed Integer Nonlinear Programming است. در مقابل این روش، روش تجزیه بندرز وجود دارد. ایده این دو روش یکسان است و حل مسئله نیازمند حل یک مسئله برنامه ریزی غیرخطی به عنوان زیر مسئله و حل یک مسئله برنامه ریزی عدد صحیح مختلط به عنوان مسئله اصلی است. ولی تفاوت ان ها در نحوه نوشتن مسئله اصلی است.
فرم کلی مدل برنامه ریزی عدد صحیح مختلط غیرخطی با عنوان MINLP1 را به صورت زیر در نظر بگیرید.

که در مدل فوق، تعاریف ذیل را داریم.

وZ^m  مجموعه m بعدی از اعداد صحیح و Rⁿ مجموعه n بعدی از اعداد پیوسته است. فرض می شود که توابع f و  g_i محدب و مشتق پذیر هستند. مجموع های S  وV به صورت زیر تعریف می شوند.

برای مقدارyⁱ ∈V ، xⁱ را جواب بهینه مسئله NLP(yⁱ)  (که در ادامه آمده است) در نظر بگیرید.

مدل MINLP1 را به صورت زیر می توان نوشت:

تعریف کنید،

مدل اصلی که با MOAV معرفی می شود براساس مجموع T به صورت زیر تعریف می شود.

اگر(x*,y*)  جواب بهینه مدل MINLP1 در نظر گرفته شود،(a*,x*,y*)   مدل * خواهد بود. می توان نشان داد که حل مسئله MOAV معادل حل مسئله MINLP1 است. در موارد اشاره شده، فرض شده است که yⁱÎY  منجر به یک جواب امکان پذیر برای  NLP(yⁱ) می شود. ولی اگر این فرض برقرار نباشد، باید بتوان به نحوی جواب yⁱ را از فضای امکان پذیر مسئله MOAV حذف کرد. برای این که نشان دهیم که yⁱ منجر به یک جواب امکان ناپذیر برای NLP(yⁱ) می شود، می توان مدل  NLPF(y) را حل کرد.

yⁱ  منجر به امکان ناپذیری مدل  NLP(yⁱ) می شود اگر NLPF(yⁱ) یک جواب امکان پذیر*>0β  داشته باشد. در این صورت محدودیت زیر را برای حذف yⁱ  از فضای امکان پذیر MOAV اضافه می کنیم.

F را مجموعه اندیس هایی تعریف کنید که yⁱÎY باعث امکان ناپذیری NLP(yⁱ) می شود. در مسئله MOVA، رابطه yÎV  باعث می شود که مقادیر امکان پذیر برای y انتخاب شود. با در نظر گرفتن محدودیت بالا، جواب های امکان ناپذیر از کلیه مقادیر y در Y حذف می شود. لذا می توان با جایگزین کردن yÎV با yÎY و محدودیت  بالا، مدل MOAV را حل کرد که از این پس این مدل را MOA می نامیم که به صورت زیر بیان می شود.

با توجه به این که محدودیت های مدل فوق به صورت مرحله به مرحله به مدل MOA اضافه می شود، لذا مدل به صورت زیر نوشته می شود.

که در مدل فوق داریم:

با توجه به مواردی که تا کنون گفته شد، می توان الگوریتم Outer Approximation را به صورت زیر بیان کرد.

برای مشاهده ادامه این درس، بسته های آموزشی این درس را به شرح ذیل تهیه نمایید.