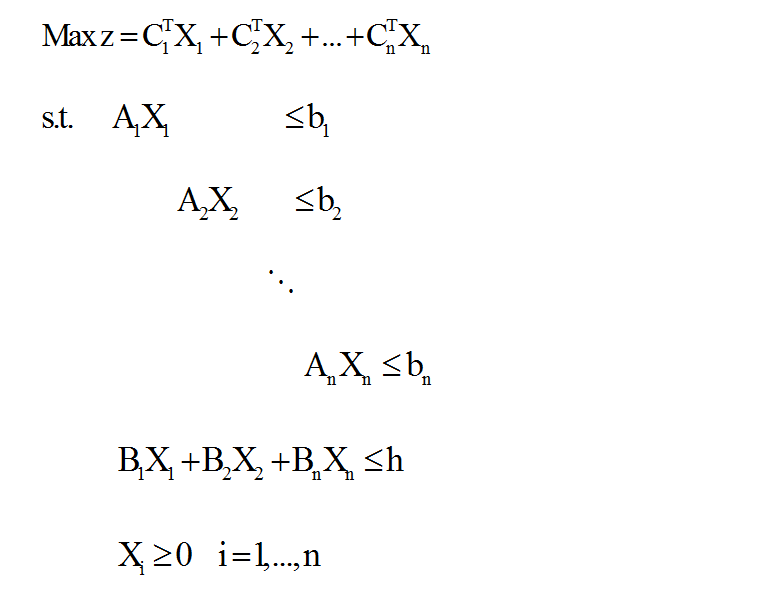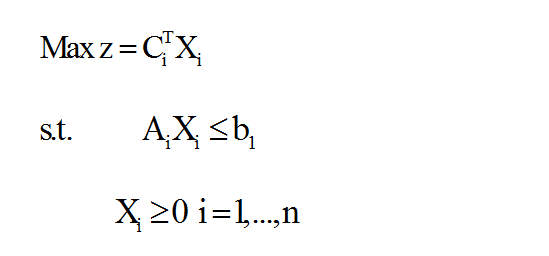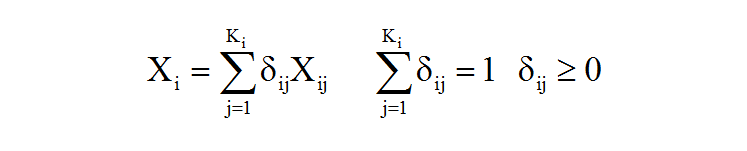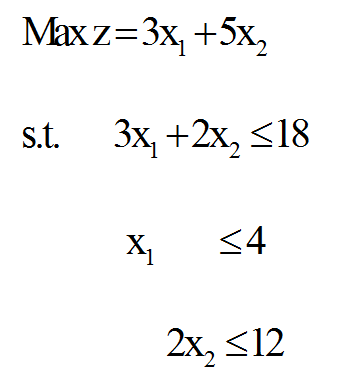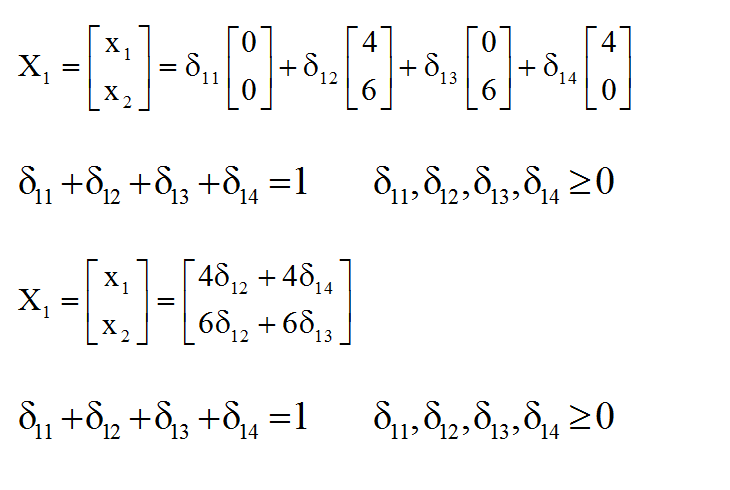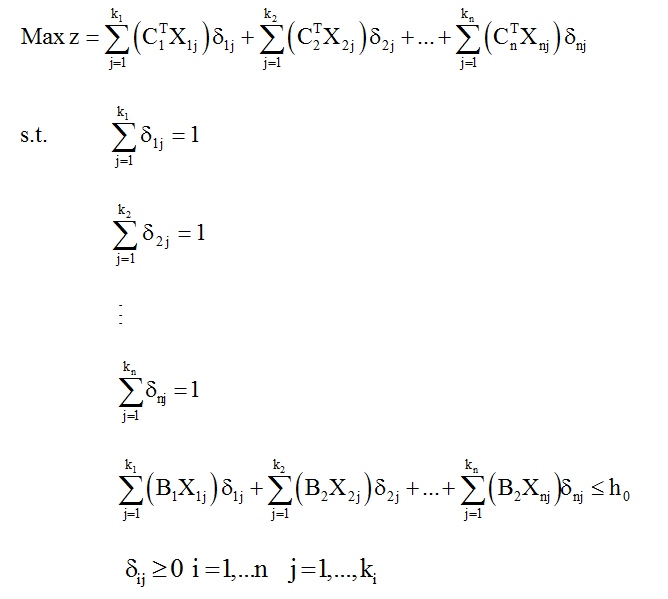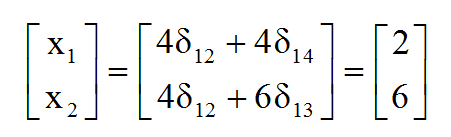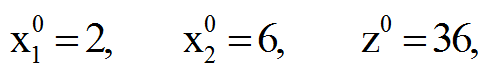درس 28: روش تجزیه دانتزیگ ولف

تهیه شده توسط گروه بهینه یاب

آ

مقدمه

الگوریتم تجزیه دانتزیگ ولف اغلب توانایی حل مسائل بسیار بزرگ را دارد. خوشبختانه برای مسائلی که ماتریس ضرایب آن ها دارای ساختار خاص زاویه ای، مانند مسائل چندبخشی، باشد کارایی این الگوریتم بسیار افزایش می یابد. مسائل چندبخشی بخش های مستقلی دارند که با تعدادی محدودیت مشترک به هم مرتبط می شوند. در این گونه مسائل، محدودیت های مشترک، محدودیت های سخت تلقی می شوند که متغیرهای هر بخش در آن ها مشاهده می شود، به طوری که حذف این محدودیت ها مسئله را به مسائلی مجزا و مستقل تبدیل می کند. هر مسئله چندبخشی ساختاری خاص به شکل زیر دارد:

در مدل بالا i=1,…,n) n) بخش داریم که تعداد متغیرهای هر بخش برابر با q_i است. h برداری ستونی با m مؤلفه (سطر) و X_i دارای q_i مؤلفه و b_i دارای m_j مؤلفه، هر B_i ماتریسی m*q_i ، هر A_i ماتریسی m_j*q_i است. توجه کنید که معادله آخر بیانگر محدودیت های مشترک بین بخش ها (بلوک ها) است و سایر معادلات، محدودیت های مختص هر بخش را نشان می دهد. از روش دانتریگ ولف می توان برای حل این گونه مسائل استفاده کرد.

الگوریتم تجزیه دانتزیگ ولف از تغییر متغیرهای تصمیم و تبدیل مسئله مدل سازی به مسئله جدیدی با عنوان مسئله اصلی یا Master Problem که فقط شامل محدودیت های سخت است، استفاده می کند. از این رو، با کاهش تعداد محدودیت ها، مسئله با تعداد تکرارهای کمتری نسبت به مسئله اولیه حل شدنی است. البته برای بررسی شرط بهینگی لازم است مسائل اضافی با محدودیت های آسان نیز حل شوند. این مسائل، مسائل فرعی الگوریتم دانتزیگ ولف نامیده می شوند.

مسئله فرعی iام مسئله چندبخشی بالا به صورت زیر است:

قضیه ۱: منطقه موجه مسائل برنامه ریزی خطی به صورت چندضلعی محدب است. در این صورت منطقه موجه هر یک از مسائل فرعی نیز چند ضلعی محدب است.

قضیه ۲: برای سادگی، فرض بر آن است که هر یک از مسائل فرعی مدل بالا دارایی منطقه موجه محدود هستند و مسئله فرعی iام دارای K_i گوشه موجه به صورت X_i1,X_i2,…X_iKi است. اندیس j،ب jامین گوشه موجه هر یک از مسائل فرعی را نشان می دهد که از ۱ تا K_i تغییر می کند. در این صورت، منطقه موجه مسئله فرعی iام را می توان به صورت ترکیب خطی محدب یا Linear Convex Combination از نقاط گوشه ای آن به صورت زیر نوشت:

برای مثال فرض کنید مسئله چند بخشی به صورت زیر باشد:

مدل بالا، دارای یک محدودیت مشترک (محدودیت اول) و یک مسئله فرعی (محدودیت دوم و سوم) است. برای به دست آوردن نقاط گوشه ای مسئله فرعی آن، به روش ترسیمی عمل می کنیم:

شکل 1- پوسته محدب یا منطقه موجه مسئله فرعی اول

هر نقطه داخل یا روی اضلاع این چهار ضلعی در شکل 1 را، که منطقه موجه مدل فرعی بالا است، می توان به صورت زیر که مجموع ترکیب محدب خطی از نقاط گوشه موجه از آن ها به صورت زیر نوشت.

توجه: مجموعه ترکیب محدب نقاط گوشه ای، پوسته محدب یا Convex Hull نامیده می شود. روشن است که مجموعه ترکیب پوسته محدب سه و چهار نقطه متمایز در صفحه که همه آن ها روی یک خط نیستند، به ترتیب تشکیل یک مثلث و مربع (مستطیل) را می دهند (شکل 2).

شکل 2- پوسته محدب سه نقطه ای و چهار نقطه ای

با جایگزین کردن X_i=Σδ_ijx_ij که در آن j=1,…, K_i برای شمارنده جمع کننده، از روی رابطه بالا به جای هر X_i که i=1,….,n و اضافه کردن محدودیت های Σδ_ij=1 و i=1,….,n که برای شمارنده i، و δ_ij≥0 به جای محدودیت A_iX_i≤b_i، مسئله چند بخشی بالا با شیوه کاهش تعداد محدودیت ها، به مسئله جدیدی برحسب δ_ij، که مسئله اصلی دانتزیگ – ولف نام دارد، به صورت زیر بازنویسی می شود:

نکته: مسئله اصلی بالا دارای m + n محدودیت یعنی برابر با تعداد محدودیت های سخت و تعداد مسائل فرعی است. به ازای هر گوشه موجه از هر مسئله فرعی، X_ij، یک متغیر به صورت δ_ij در مسئله اصلی در نظر می گیریم.

در مثال بالا، با جایگزین کردن مقدار x₁ بر حسب روابط بالا در تابع هدف و محدودیت های مشترک مسئله و در نظر گرفتن 1= Σδ_1j که j=1,…,4 و δ_1j≥0، تعداد محدودیت های مسئله به دو محدودیت زیر کاهش خواهد یافت:

مدل جدید بالا، مسئله اصلی دانتزیگ – ولف نام دارد. هر مسئله تبدیل یافته، یک مسئله برنامه ریزی خطی بوده که با استفاده از روش سیمپلکس به راحتی حل شدنی است. با حل این مدل، δ₁₂=0.5 و δ₁₃=0.5 و سایر متغیرها برابر با صفر هستند؛ از این رو خواهیم داشت:

بنابراین جواب بهینه این مسئله عبارت است از:

نکته: دقت کنید که در این روش، به ازای هر بخش با هر تعداد محدودیت فقط یک محدودیت جدید یعنی 1= Σδ_1j که j=1,…,4 به نام قید تحدب اضافه می شود. همچنین، به ازای هر تعداد محدودیت مشترک به همان تعداد محدودیت جدید تولید می کنیم.

با توجه به بالا بودن تعداد نقاط گوشه ای به خصوص در مسائل بسیار بزرگ، معمولا به دلایل مختلفی امکان شناسایی این نقاط وجود ندارد. خوشبختانه در روش دانتزیگ- ولف نیازی به دانستن تمام نقاط گوشه ای هر یک از مسائل نیست و می توان با روش تولید ستون یا Column Generation، ستون مورد نیاز (ستون ورودی) را به دست آورد.