برای دانلود خلاصه آموزش تئوری صف لطفا ایمیل خود را وارد کنید تا این آموزش برای شما ارسال شود.
درس 24: تئوری صف
تهیه شده توسط گروه بهینه یاب
آموزش تئوری صف
مقدمه
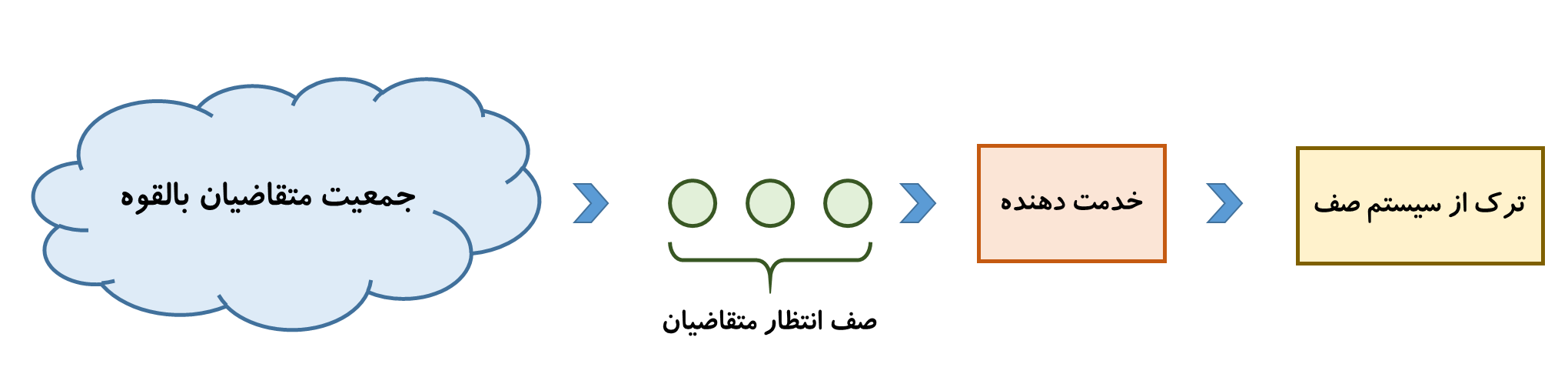
شبیهسازی غالبا در تحلیل مدلهای صف به کار می رود. در یک مدل ساده ولی رایج صف(مشابه شکل 1)، متقاضیان از زمانی به زمان دیگر وارد سیستم میشوند، به صف انتظار می پیوندند، سپس خدمت دریافت میکنند و سرانجام سیستم را ترک میکنند. واژه “متقاضی” اشاره به هر نوع نهادی دارد که خواهان دریافت “خدمت” از سیستم باشد. بنابراین، تشکیلات خدماتی، سیستمهای تولید، تشکیلات نگهداری و تعمیر سیستمهای ارتباطات و کامپیوتر و سیستمهای حمل و نقل مواد را میتوان به منزله سیستمهای صف نگریست.
مدلهای صف صرفنظر از این که از طریق ریاضی حل یا از طریق شبیهسازی تحلیل شوند، ابزاری نیرومند را برای طراحی و ارزیابی عملکرد سیستمهای صف در اختیار تحلیل گر قرار می دهند. از معیارهای رایج عملکرد سیستم میتوان به ضریب بهره برداری خدمت دهنده که همان درصدی از زمان که خدمت دهنده مشغول است، طول صفهای انتظار و مدت انتظار متقاضیان در صف را در بر میگیرد.
در بسیاری از موارد، به هنگام طراحی یا در تلاش برای اصلاح سیستم صف، تحلیل گر یا تصمیم گیرنده با ایجاد توازن بین ضریب اشتغال خدمت دهنده و میزان جلب رضایت متقاضی که رابطه مستقیم با طول صف و مدت انتظار در صف دارد، به اصلاح سیستم می پردازد. به منظور پیش بینی معیارهای عملکرد سیستم بر حسب تابعی از پارامترهای ورودی، از نظریه صف و یا شبیهسازی استفاده میکنند. از جمله پارامترهای ورودی میتوان به موارد زیر اشاره کرد:
- آهنگ ورود متقاضی به سیستم
- نوع خدمت دهی به متقاضی
- سرعت خدمت دهی
- تعداد خدمت دهندهها
- نظام خدمت دهندهها
برخی از پارامترهای ورودی تا حدی توسط مدیریت به طور مستقیم قابل کنترل و مهار است. اگر رابطه بین معیارهای عملکرد و پارامترهای ورودی در مورد سیستم در دست بررسی به طرز مناسبی شناسایی شده باشد، معیارهای عملکرد به طور غیرمستقیم توسط مدیریت پارامترهای ورودی قابل کنترل خواهد بود.
در مورد سیستمهای نسبتا ساده، میتوان معیارهای عملکرد را از طریق معادلات تحلیلی به فرم بسته برآورد کرد که در مقایسه با کاربرد مدل شبیهسازی متضمن صرفه جویی قابل توجهی در وقت و هزینه است. اما برای ایجاد مدلهای واقع بینانه و سیستمهای پیچیده معمولا نیاز به شبیهسازی وجود دارد. با وجود این، مدلهای تحلیلی علی رغم نیاز به فرضهای ساده کننده فراوان، در ارایه سریع برآورد های تقریبی در مورد عملکرد سیستم ارزشمند است. سپس، میتوان با استفاده از مدل تفضیلی و واقع بینانه شبیهسازی، برآورد های فوق را بهبود بخشید.
آموزش تئوری صف
ویژگیهای سیستم صف
عناصر عمده سیستم عبارتند از: متقاضیان و خدمت دهندهها. واژه “متقاضی” را میتوان به مردم، خودروها، کامیونها، کارگران ساختمان، بیماران، پالتها، هواپیما، جعبهها، سفارشها، یا البسه چرک و به طور کلی هر آنچه به منظور دریافت خدمت به امکاناتی نیاز دارد تعبیر کرد. واژه “خدمت دهنده” را میتوان به راهنما، تعمیرکار، مکانیک خودرو، پزشک، ماشین خودکار انبار کردن و دریافت از انبار، باند فرودگاه، دستگاه خودکار بسته بندی، ماشین لباس شویی و به طور کلی هر کس یا دستگاهی که خدمت مورد نیاز را ارایه میکند، تعبیر کرد.
جمعیت متقاضی
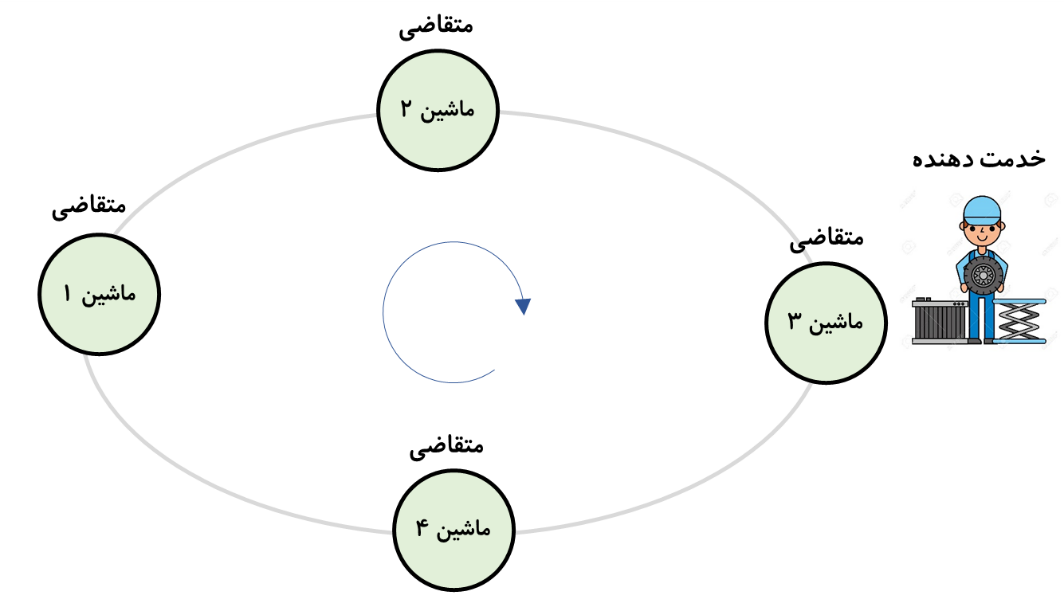
جمعیت متقاضیان بالقوه که به آن جمعیت متقاضی گفته میشود ممکن است متناهی یا نامتناهی باشد. برای جمعیت متقاضی متناهی این مثال را در نظر بگیرید. مثلا، مجموعه ای متشکل از 4 ماشین را در نظر بگیرید که عمل آوری لاستیک خودرو را انجام می دهند. با گذشت یک فاصله زمانی، هر ماشین به طور خودکار باز میشود و کارگری لاستیک موجود در آن را بیرون میآورد و یک حلقه لاستیک پخته نشده در داخل آن قرار می دهد. ماشینها همان متقاضیان هستند که در لحظه باز شدن دستگاه، عمل وارد شدن به سیستم انجام میشود. کارگر همان خدمت دهنده است که به ماشینهای باز شده خدمت می دهد. جمعیت متقاضی متناهی و متشکل از 4 ماشین است که در شکل 2 نمایش شماتیک آن آورده شده است.
آموزش تئوری صف
در بسیاری از سیستمها با جمعیت بزرگ، معمولا جمعیت متقاضی نامتناهی فرض میشود. این فرض در مورد چنین سیستمهایی معمولا ضرر ندارد و باعث میشود که سیستم را ساده کند. مثالهای از جمعیتهای نامتناهی شامل متقاضیان بالقوه یک رستوران، بانک، و خدمت دهندهها میتواند مانند باجههای سفارش غذا و باجههای بانک اشاره کرد.
نکته: اگر چه جمعیت واقعی ممکن است متناهی ولی بزرگ باشد، به طور کلی استفاده از مدلهای مرتبط به جمعیت نامتناهی بدون ایراد است مشروط بر این که تعداد متقاضیان در حال دریافت خدمت یا منتظر در صف برای خدمت گیریی در هر لحظه نسبت به جمعیت متقاضیان بالقوه کوچک باشد.
تفاوت اصلی بین مدلهای جمعیت متناهی و نامتناهی در این است که آهنگ ورود چگونه تعریف شود. در مدل جمعیت نامتناهی، آهنگ ورود (یعنی متوسط تعداد ورود در واحد زمان) تحت تاثیر تعداد متقاضیانی که جمعیت متقاضی را ترک میکنند و به سیستم صف می پیوندند قرار نمیگیرد.
نکته: اگر دوره هجوم بر متقاضیان وجود نداشته باشد، آهنگ ورود را ثابت در نظر میگیریم.
آهنگ ورود به سیستم صف در مدلهای جمعیت متناهی متقاضیان قطعا به تعداد متقاضیان در حال خدمت گیری یا منتظر در صف بستگی دارد. جمعیت متقاضی میتواند شامل یک عضو باشد. مثلا هواپیمای شخصی رییس جمهور را در نظر بگیرید. وقتی گروه تعمیرکارانی که 24 ساعته آماده ارایه خدمت هستند در حال خدمت دهی به این هواپیما هستند، آهنگ ورود صفر است، زیرا هیچ متقاضی بالقوه دیگر وجود ندارد تا به تشکیلات نگهداری مراجعه کند.
ظرفیت سیستم
آموزش تئوری صف
در بسیاری از سیستمهای صف، حدی برای تعداد متقاضیانی که میتوانند در صف انتظار یا در سیستم قرار گیرند وجود دارد. مثلا، یک کارواش خودکار ممکن است تنها دارای فضا برای ده خودرو در صف انتظار باشد. ممکن است توقف خودروها در خیابان بسیار خطرناک یا خلاف مقررات است. یک متقاضی تازه وارد که سیستم را پر بیابد، وارد آن نمیشود و فورا به جمعیت متقاضی برمیگردد. برخی از سیستمها مانند سیستم ثبت نام دانشجویان را میتوان دارای ظرفیت نامحدود به شمار آورد. محدودیتهایی در مورد تعداد دانشجویانی که مجاز به قرار گرفتن در صف انتظار هستند وجود ندارد. چنانکه بعدا خواهیم دید، هر گاه ظرفیت سیستم محدود باشد تمیز بین آهنگ ورود (همان تعداد مراجعه به سیستم در واحد زمان) و آهنگ موثر ورود (همان تعداد موارد مراجعه به سیستم و ورود آنی در واحد زمان) ضروری است.
فرآیند ورود
فرآیند ورود برای مدلها با جمعیت نامتناهی، معمولا بر حسب مدتهای بین ورود متقاضیان متوالی مشخص میشود. ورودها ممکن است در لحظات از قبل تعیین شده (همان قطعی) یا در لحظات تصادفی روی دهند. اگر ورود در لحظات تصادفی صورت گیرد، معمولا مدتها بین ورود با توزیع آماری مشخص میشوند. علاوه بر این، متقاضیان میتوانند یک به یک یا به صورت گروهی وارد شوند. اندازه یک گره ممکن است ثابت یا متغیر و تصادفی باشد.
مهمترین مدل مربوط به ورود تصادفی فرایند ورود پواسون است. اگر مدت بین ورود متقاضی n-1 و متقاضی n با An معرفی شود(A1 لحظه واقعی ورود اولین متقاضی است)، در مورد فرایند ورود پواسون، An توزیع آماری نمایی با میانگین 1-λ واحد زمان دارد. آهنگ ورود λ متقاضی در واحد زمان است. تعداد ورود در فاصله زمانی به طول t یعنی (N(t، توزیع پواسون با میانگین λ متقاضی دارد.
فرایند ورود پواسون به عنوان مدل ورود مردم به رستورانها، اتوبانکها و سایر تشکیلات خدماتی، ورود تقاضاهای تلفنی به مرکز هدایت مشتری، ورود تقاضا یا سفارش برای یک خدمت یا کالا و ورود قطعات یا ماشین آلات از کار افتاده به تعمیرگاه مورد استفاده قرار گرفته است.
آموزش تئوری صف
رفتار صف و قانون
منظور از رفتار صف، کنشهای متقاضی تا زمان شروع خدمت گیری در صف انتظار است. در برخی موارد این امکان وجود دارد که متقاضی تازه از راه رسیده بلافاصله (با مشاهده صفی بسیار طولانی) یا با تاخیر ( پس از مشاهده حرکت بسیار کند صف) از پیوستن به سیستم یا ماندن در آن منصرف شود و یا (پس از مشاهده این که در صفی است که آرام حرکت میکند) تغییر صف بدهد.
منظور از قانون صف، ترتیب منطقی متقاضیان در صف است و تعیین میکند که با آزاد شدن یک خدمت دهنده کدام متقاضی باید برای خدمت گیری انتخاب شود. قوانین رایج صف مشتمل بر خدمت گیری به ترتیب ورود (FIFO یا First In First Out)، به عکس ترتیب ورود (LIFO یا Last In First Out)، به ترتیب تصادفی (SIRO یا Served In Random Order)، براساس کوتاهترین مدت مورد نیاز (SPT یا Shortest Processing Time First)، و براساس اولویت (PR یا Priority) است.
آموزش تئوری صف
مدتهای خدمت دهی و مکانیزم آن
مدتهای خدمت دهی به ورود کنندگان با نمادهای S1،S2،S3، … نشان داده میشود. این مدتها میتواند ثابت یا تصادفی باشند. در حالت تصادفی، معمولا دنباله ،{…,S1،S2،S3} دنباله ای از متغیرهای تصادفی مستقل و هم توزیع هستند. توابع توزیع نمایی، ویبول، گاما، و نرمال همگی میتوانند به عنوان توابع توزیع برای مدت خدمت گیری مورد استفاده قرار گیرد.
هر سیستم صف از تعدادی مرکز خدمت دهی و صفهای مرتبط کننده آنها تشکیل میشود. هر مرکز خدمت دهی مشتمل است بر تعدادی خدمت دهنده به تعداد c که به صورت موازی فعالیت دارند. موازی بودن به این معنا است که متقاضی با رسیدن به سر صف، هر متقاضی اولین خدمت دهنده بیکار را انتخاب میکند. تعداد خدمت دهنده میتواند از یک تا نامحدود تغییر کند.
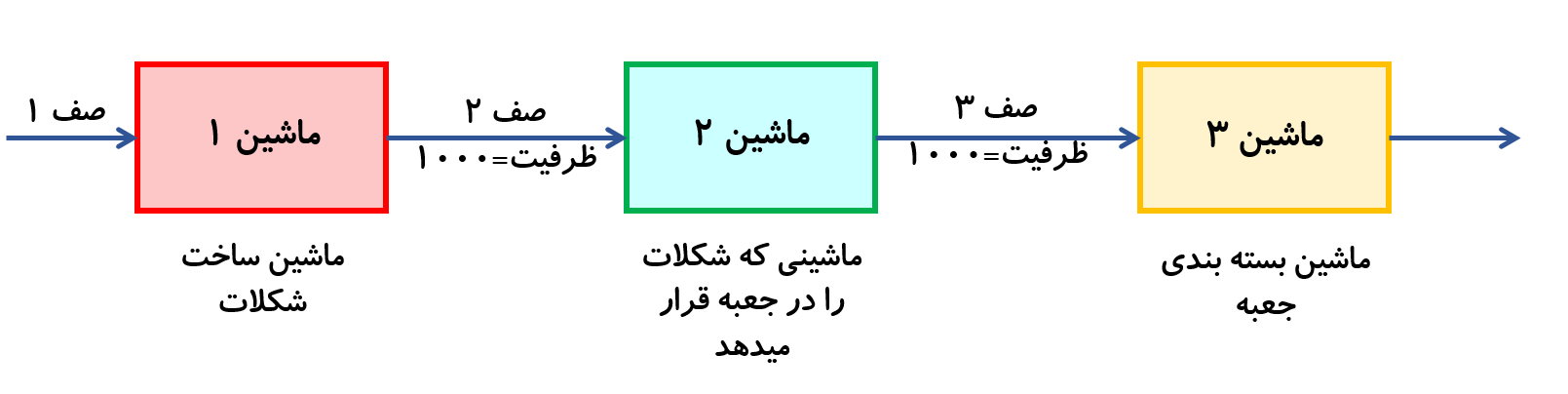
مثال 1: خط تولید یک واحد ساخت شکلات سه دستگاه ماشین را در بر میگیرد. ماشین اول قطعات شکلات را تولید و در بسته خود قرار می دهد. ماشین دوم هر 50 قطعه شکلات را در یک جعبه میگذارد و ماشین سوم جعبه را کاملا می بندد و آن را در سلفون قرار می دهد. هر یک از دو انبار میان خدمت دهندهها ظرفیت 1000 جعبه را دارد. در شکل 3 این سیستم نمایش داده شده است. سیستم سه مرکز خدمت دهی و هر مرکز یک خدمت دهنده همان c=1 دارد و ظرفیت صفهای بین ماشینها نیز دارای محدودیت است. چنین فرض میشود که در صف اول همواره موجودی کافی ماده خام در دست است. به سبب محدودیت ظرفیت صف، هر گاه که موجودی ماشین 2 پر شود، ماشین 1 متوقف میشود و حال آنکه با خالی شدن همین صف، ماشین 2 متوقف میشود. به طور خلاصه، سیستم سه صف تک مجرایی زنجیره ای با محدودیتهای ظرفیت صف و جریان پیوسته ورود به اولین صف را در بر میگیرد.
نمادگذاری سیستمهای صف
با توجه به تنوع سیستمهای صف، در ادبیات نظریه صف روالی برای معرفی سیستمهای موازی صف پیشنهاد کرده که به طور وسیع مورد استفاده قرار میگیرد. نسخه اختصاری چنین عرفی مبتنی بر شکل A/B/c/N/K است. این حروف معرف مشخصههای زیر برای سیستم صف است که در ادامه تعریف میشود:
A: نشان دهنده توزیع فواصل بین ورود است.
B: معرف توزیع مدت خدمتدهی است.
c: نشان دهنده تعداد خدمت دهندههای موازی است.
N: معرف ظرفیت سیستم است.
K: نشان دهنده اندازه جمعیت است.
نکته: علایم مرسوم برای A و B عبارت اند از M(نمایی)، D(ثابت یا قطعی)، Ek (ارلنگ مرتبه k) و G (عمومی یا دلخواه).
مثلا M/M/1/∞/∞/M معرف سیستمی با یک خدمت دهنده است که ظرفیت صف آن نامحدود و جمعیت متقاضیان بالقوه آن نیز نامتناهی باشد. مدتهای بین ورود و مدتهای خدمت دهی نیز توزیع نمایی دارند. هر گاه N و K نامتناهی باشند میتوان آنها را از انتهای علامت فوق حذف کرد. مثلاM/M/1/∞/∞/M را اغلب به صورت کوتاه M/M/1 می نویسند.
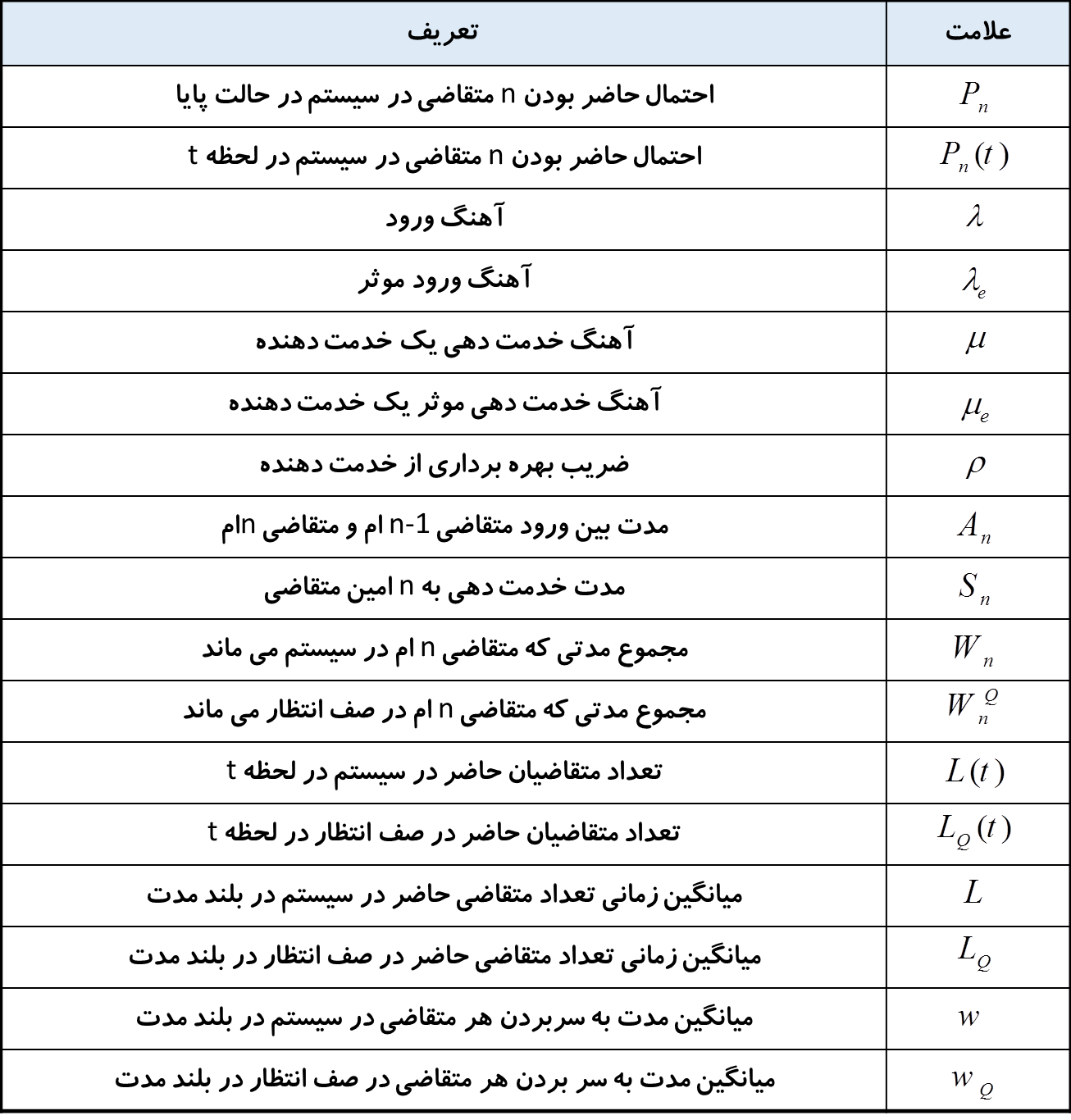
برای ارایه نظریه صف نیاز به معرفی علایم خاصی است که در جدول زیر ارایه میشود.
رفتار گذرا و پایای سیستمهای صف
سیستم M/M/1/1/∞/M را در نظر بگیرید که در لحظه صفر خالی و بدون فعالیت است. به عبارت دیگر، یک صف تک مجرایی با ورودهای پواسون با میانگین ورود λ در واحد زمان و مدتهای خدمت دهی نمایی با میانگین 1-μ واحد زمان در نظر بگیرید. ظرفیت سیستم برابر با یک است به طوری که هرگز صف انتظار تشکیل نمیشود و متقاضیان از جمعیت نامتناهی که خدمت دهنده را مشغول بیابند برمیگردند.
مثال 2: یک سکوی بارگیری را در نظر بگیرید که فضایی برای یک کامیون دارد و فاقد جا برای تشکیل صف انتظار است. اگر کامیونی در سکوی بارگیری باشد، تمام کامیون هایی که وارد میشوند باید به سکوهای دیگر بروند. هر گاه کامیونی وارد شود یا از سکو دور میشود و به محل دیگری برای تخلیه می رود و یا تخلیه آن سریعا شروع میشود.
کامیونها طبق توزیع پواسون با میانگین λ=2 در ساعت وارد میشوند، در حالی که بارگیری و یا تخلیه در قالب متغیر تصادفی نمایی با میانگین μ-1=120 دقیقه است، به طوری که آهنگ خدمت دهی معادل μ=0.5 در ساعت است. چون جمعیتی بسیار بزرگ از کامیونها متقاضی به صورت بالقوه وجود دارد، مدلی برای سیستم صف M/M/1/1/∞/M تهیه میشود. در ادامه از طریق شبیهسازی این سیستم مورد بررسی قرار میگیرد.
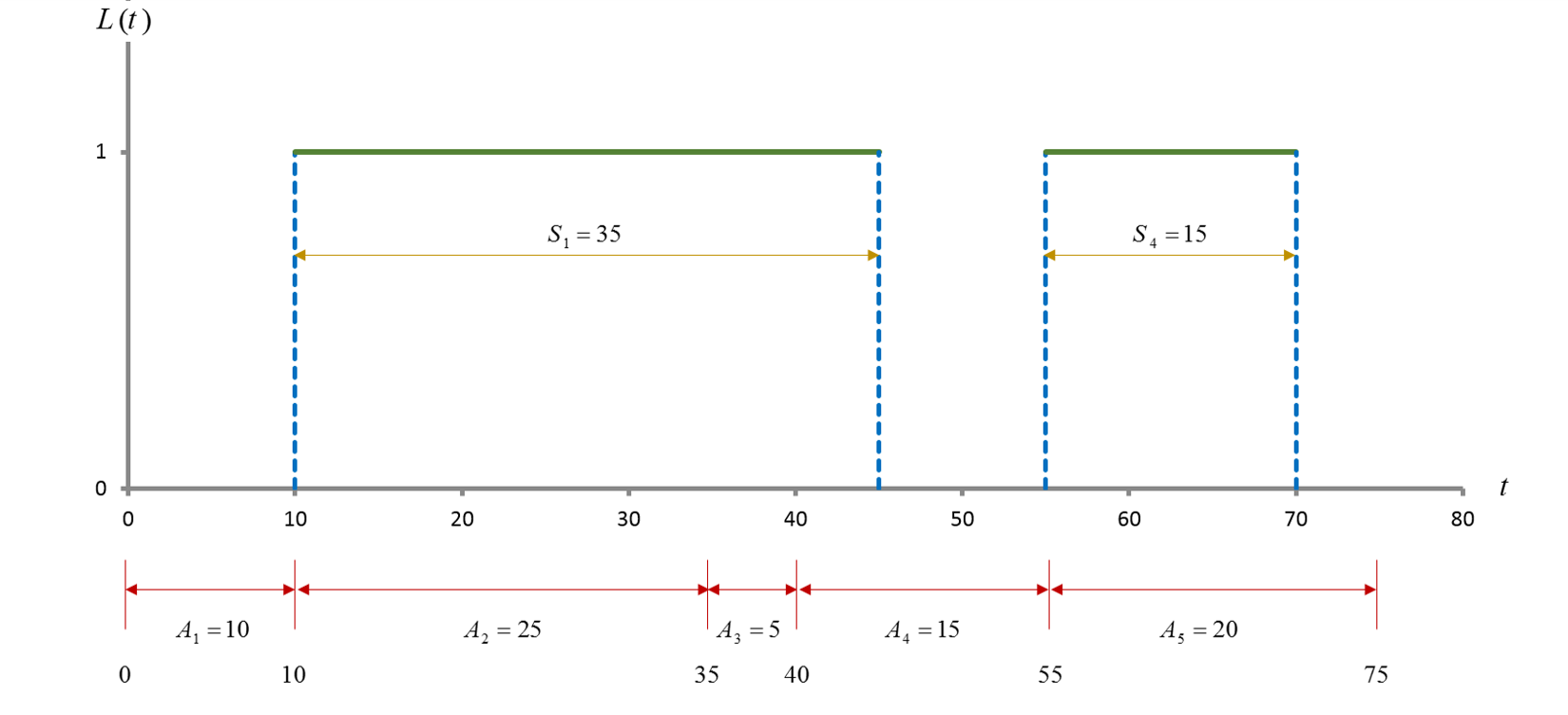
فرض کنید سکو در لحظه صفر خالی است. به علاوه فرض کنید که مدتهای بین ورود تولید شده و بر حسب دقیقه عبارت از A1=10، A2=25 ،A3=5 ،A4=15 ، A5=20 است. مدتهای خدمت دهی نیز تولید شده و بر حسب دقیقه عبارت از S1=35، S2=20 ،S3=60 ،S4=15 ، S5=35 است. نمایشی از تغییرات (L(t که همان تعداد کامیونهای حاضر در لحظه t است در شکل زیر نشان داده شده است.