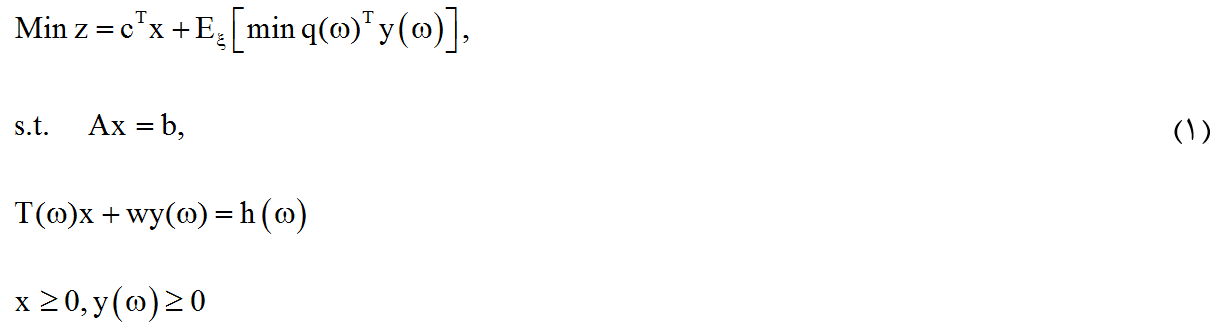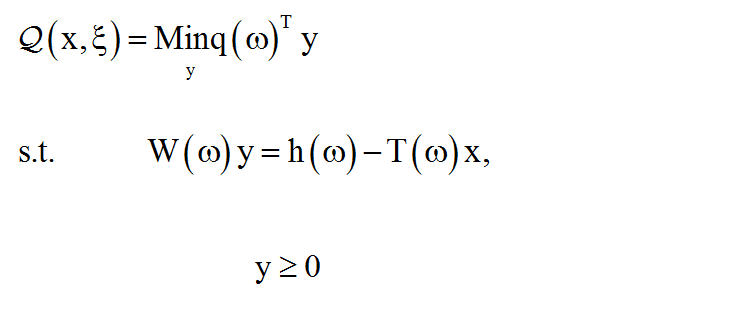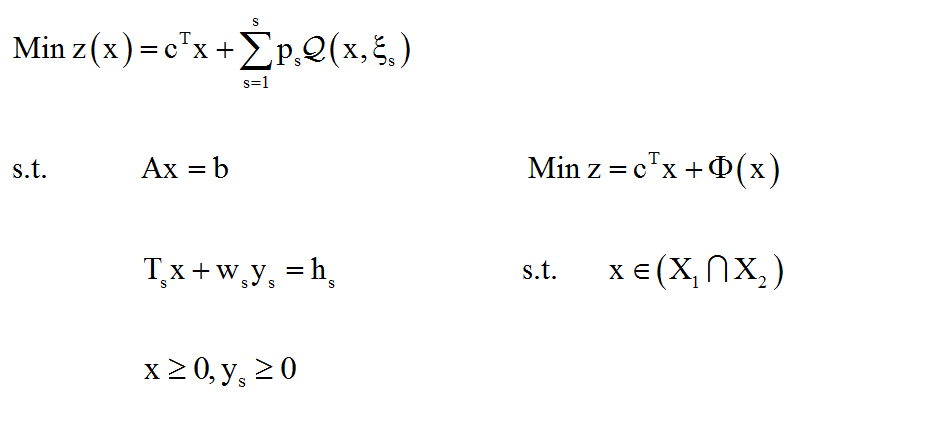درس 27: برنامه ریزی احتمالی

تهیه شده توسط گروه بهینه یاب

آ

مقدمه

برنامه ریزی احتمالی متعلق به شاخه عمومی تر برنامه ریزی عدم اطمینان است که شامل مباحثی همچون برنامه ریزی پویا، درخت تصمیم گیری، شبیه سازی، فرایندهای تصادفی و قیود احتمالی است. در تمام مسائل برنامه ریزی خطی، غیر خطی، عدد صحیح و صفر و یک؛ قطعیت داده ها یک فرض اصلی است و لذا آن را برنامه ریزی قطعی می نامیم. دشواری این مدل ها بیشتر به خاطر یافتن جواب بهینه است که با عنوان بهینه سازی برنامه ریزی احتمالی نامیده می شود و به خصوص در مسائل برنامه ریزی غیر خطی و عدد صحیح این دشواری بیشتر و بیشتر می شود.. هر گاه در یک مسئله برنامه ریزی، عدم اطمینان به شکل توزیع های پیوسته یا گسسته احتمالی در پارامترهای مدل وجود داشته باشد، آن را یک مسئله برنامه ریزی احتمالی می نامیم. معمولا در نظر گرفتن پارامترهای عدم اطمینان باعث بزرگی و پیچیدگی بهینه سازی آن می شود. برخی مواقع برای ساده سازی مسئله، پارامترهای عدم اطمینان را با مقدار متوسط آن و یا برآوردی از آن جایگزین می کنند که می تواند به خطای فاحش در نتایج منجر شود، چون این جواب اند برای همین مقادیر معتبر است و ممکن است برای مقادیر دیگر غیر موجه یا غیر بهینه باشد.

برنامه ریزی احتمالی دو مرحله ای با بازگشت

در برنامه ریزی احتمالی دو مرحله ای، متغیرهای تصمیم گیری مسئله بهینه سازی در شرایط عدم اطمینان، به دو مجموعه تقسیم می شوند. متغیرهای مرحله اول (x) متغیرهایی هستند که باید قبل از وقوع و محقق شدن پارامترهای تصادفی، در مورد آن ها تصمیم گیری شود. هنگام تصمیم گیری و حل مدل، این تصمیمات در حضور عدم اطمینان در مورد رخدادهای آتی (ξ) گرفته می شود. در مرحله دوم که در مورد متغیرهای مرحله دوم تصمیم گیری می شود، مقدار واقعی پارامترهای عدم اطمینان (ξ)، مشخص و واقع می شوند و تصمیمات بازگشتی یا اقدامات اصلاحی (y) صورت می گیرد. به دلیل این عدم اطمینان، هزینه مرحله دوم، خود یک متغیر تصادفی خواهد بود.

در واقع، تصمیمات مرحله اول با در نظر گرفتن تأثیرات آتی آن ها بر روی تصمیمات مرحله دوم گرفته می شود. این تأثیرات با تابع بازگشت اندازه گیری می شود که متوسط مقدار هزینه تصمیمات مرحله دوم را اندازه گیری می کند.

فرموله بندی برنامه ریزی احتمالی

مسئله برنامه ریزی خطی احتمالی با بازگشت ثابت به صورت زیر فرموله می شود:

در رابطه بالا، c برداری مشخص و قطعی با n₁ مؤلفه (عنصر)، b برداری قطعی با m₁ مولفه، A و W ماتریس های مشخص و معین به ترتیب با ابعاد m₁*n₁ و m₁*n₁ هستند؛ عبارت W، ماتریس بازگشت نامیده می شود که فرض می کنیم در اینجا ثابت است. در صورت مشخص و ثابت بودن ماتریس باز گشت، این نوع برنامه ریزی را برنامه ریزی احتمالی دو مرحله ای با بازگشت ثابت می نامیم.

برای هر q(ω)، ω برداری با n₂ مؤلفه، (h(ω برداری با m₂ مؤلفه و (T(ω ماتریسی m₂*n₁ است. در واقع، q بردار ضرایب است و W، h و T، ماتریس های ضرایب هستند که ممکن است به متغیرهای تصادفی (ω) وابسته و تابعی از آن باشند. با کنار هم قرار دادن اجزاء تصادفی مسئله بالا، به بردار پارامترهای احتمالی (ξ^T(ω (به صورت زیر) با (N=n₂+m₂+(m₂*n₁ عنصر می رسیم؛ در این بردار (T_i(ω ،بi امین سطر ماتریس ضرایب تکنولوژی (T(ω است.

توجه: در حالت کلی محدودیت ها می توانند از نوع ≤ و = و ≥ و مسئله از نوع حداکثر سازی و حداقل سازی باشد.

مدل (1) معادل برنامه ریزی قطعی زیر است:

که داریم:

متوسط هزينه تصمیمات مرحله دوم با (Φ(x نشان داده می شود و آن را تابع بازگشت می نامیم که برای یک x معین و بر حسب ω به دست می آید. در این رابطه، E_ω میانگین ریاضی است که بر روی فضای (ξ(ω به دست می آید. همچنین تابع (Ο(ξ(ω),x به ازای یک x و (ξ(ω معین و ثابت به دست می آید؛ به عبارت دیگر، با توجه به اینکه مقدار x از تصمیمات مرحله اول به دست آمده، مقدار آن در محاسبه این تابع ثابت است؛ از این رو، برای هر معین، یک قابل محاسبه است. به ازای هر (Ο(ξ(ω),x که محاسبه می شود، یک مقدار برای تصمیمات مرحله دوم به صورت بهینه که با (y) نشان می دهیم، داریم. در مسائل برنامه ریزی دو مرحله ای محاسبه تابع بازگشت بسیار مشکل است. چون در تابع (Ο(ξ(ω),x ، به ازای هر ω مقدار (y(ω از حل رابطه بالا به دست می آید.

در مسئله کشاورز که در ادامه مورد بررسی قرار می گیرد، متغیر x زمین تخصیص داده شده به هر محصول، متغیر y مقدار خرید و فروش محصولات مختلف؛ و ξ مقدار بازدهی محصولات که احتمالی هستند. ماتریس ،(T(ω و بردار (h(ω احتمالی بوده و قیمت (q) مقداری ثابت هستند.

توجه: روابط (1) تا (4) قابلیت استفاده برای متغیرهای تصادفی گسسته و پیوسته را دارند.

در صورت قطعی بودن ماتریس T، رابطه بالا به صورت زیر بازنویسی می شود:

در این رابطه، داریم:

روشن است که ماهیت مشکل برنامه ریزی احتمالی به دلیل بار محاسباتی محاسبه (Φ(x برای همه xها در روابط (2) تا (4) یا (Ψ(χ برای همه χ در رابطه (5) است. از این رو، ویژگی های برنامه معادل قطعی آن ها و توابع (Φ(x و (Ψ(χ به طور گسترده ای مورد تحقیق قرار گرفته است. البته هنگامی که ساختار بازگشت همانند مسائل با بازگشت ثابت باشد، با این مشکلات کمتر مواجهیم. در بخش های بعدی برخی از این ویژگی ها را بررسی می کنیم.

مسئله با بازگشت ثابت

به معنی این است که ماتریس بازگشت (W) مستقل از ω باشد، یعنی داشته باشیم W(ω)=W. این ویژگی اجازه می دهد تا به راحتی منطقه موجه را برای محاسبات مشخص کنیم. در صورت ثابت نبودن این ماتریس، ممکن است با مشکلاتی روبه رو شویم که در ادامه به آن ها می پردازیم.

نکته: وضعیتی که در آن [W=[I,-I باشد، مسئله با باز گشت ساده نامیده می شود. I ماتریس همانی است.

مسئله با بازگشت کامل

یک مسئله با بازگشت کامل است، اگر ماتریس بازگشت ثابت باشد و به ازای هر مقدار برای تصمیمات مرحله اول (x) محدودیت مسئله مرحله دوم، (T(ω)x+Wy(ω)=h(ω، موجه باقی بماند. روشن است که در این گونه مسائل به ازای هر مقدار برای x و متغیر تصادفیω ، مسئله مرحله دوم همواره موجه باقی می ماند.

مثال 1: مسئله برنامه ریزی احتمالی دو مرحله زیر را در نظر بگیرید:

ξ_k یک توزیع گسسته یکنواخت است و برای آن، 11=k پیشامد بین صفر و 1- داریم. وجود و احتمال وقوع هر پیشامد P_k=1/11 است (k=1,2,…,11). توجه کنید در این مسئله عبارت (ω) با اندیس k آورده شده است. آیا این مدل یک مسئله بازگشت کامل است؟

حل:

در مرحله اول مسئله برنامه ریزی احتمالی دو مرحله ای بالا در مورد متغير تصميم x تصمیم گیری می کنیم. از این رو، این متغیر، متغير تصمیم مرحله اول است؛ در مرحله دوم پس از مشخص شدن مقدار ξ_k ، در مورد متغیرهای تصمیم مرحله دوم تصمیم گیری می شود. توجه کنید به ازای هر k=1,2,…,11،بy_1k,y_2k,y_3k,y_4k متغیرهای تصمیم مرحله دوم هستند. در زیر این مسئله را به صورت ماتریسی بیان کرده ایم:

با توجه به ثابت بودن ماتریس بازگشت به ازای همه k، این مسئله یک مسئله با بازگشت ثابت است. علاوه بر این ماتریس فنی نیز به ازای همه k ثابت است.

در این مسئله برای (Ο(ξ,x داریم:

برای نمونه، به ازای ξ₁=0 (اولین مقدار گسسته) و x=5، داریم:

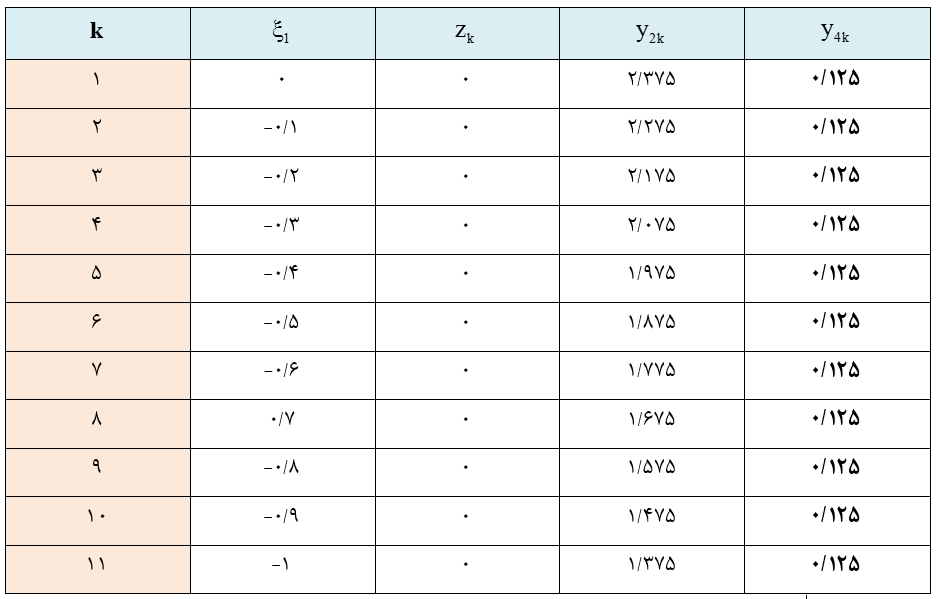
مقدار هدف آن، z=0 است، که به ازای x=5 و ξ₁=0 به دست آمده است. نتایج همه مسائل به ازای 5 = x و ξ_k مختلف در جدول (1) خلاصه شده است. در این جدول، متغیرهای y_k1 و y_k3 برابر با صفر و آورده نشده اند.

جدول (1) تعیین موجه بودن مرحله دوم

چون به ازای همه مقادیر متغیرهای مرحله اول، مدل مرحله دوم امکان پذیر است لذا یک مدل دومرحله ای کامل داریم.

برنامه ریزی احتمالی دو مرحله ای با پارامترهای تصادفی گسسته

در نظر گرفتن ξ به صورت یک متغیر تصادفی گسسته، از مهم ترین کلاس های برنامه ریزی احتمالی است که در عمل مستقیم یا از طریق نمونه گیری از یک توزیع پوسته مکرر استفاده می شود. ویژگی هایی که در این قسمت در قالب قضیه گفته می شود، در قسمت های دیگر استفاده می شوند.

مجموعه {X₁={x|Ax=b,x≥0، مجموعة موجه مرحله اول است که با محدودیت های ثابت مرحله اول مشخص می شوند؛ این مجموعه به بردار متغیرهای تصادفی وابسته نبوده و برای همه آن ها ثابت است. به ازای هر ξ معین، مجموعه موجه اولیه را به صورت زیر تعریف می کنیم:

حال با فرض گسسته بودن ξ، مجموعه موجه مرحله دوم را تعریف می کنیم:

در واقع X₂ متغیرهای تصمیمی (x) را در بر می گیرد که در مرحله دوم موجه هستند. در مثال 1 ای که قبلا به آن اشاره شد، {X₁={x|x≤5,x≥0 مجموعة موجه مرحله اول بود. مجموعه موجه مرحله دوم نیز با توجه به اینکه به ازای کلیه مقادیر برای α محدودیت ها همچنان موجه باقی می ماند، از این رو {X₂={R در واقع، مسئله مذکور یک مسئله با باز گشت کامل است.

در این صورت، قضایای زیر را داریم:

قضيه 1: به ازای یک ξ معين، مجموعه موجه اولیه، ξ}=X₂}، یک چند وجهی محدب است.

قضیه 1-2: وقتی ξ، یک متغیر تصادفی گسسته محدود باشد، X₂ یک چند وجهی محدب است.

قضیه 1-3: اشتراکی چند وجهی های متناهی، یک چند وجهی متناهی است.

همان طور که گفته شد به ازای مقدار ثابت x و ξ ، مقدار برنامه مرحله دوم،(Ο(ξ(ω),x، به صورت زیر مشخص می شود:

در محاسبه مقدار (Ο(ξ(ω),x، وقتی با مشکل روبه رو می شویم که رابطه بالا نامتناهی (بی کران) یا ناموجه باشد. نامحدود شدن این مقدار، معمولا از تعریف بد مدل ناشی می شود که می توانیم به راحتی با افزودن یک کران بالا بر روی آن را برطرف کنیم. در صورت ناموجه شدن این تابع، اگر فقط x ∈ X₂ را در نظر بگیریم، مشکل موجه بودن نیز حل می شود. بنابراین، به ازای x ∈ X₂ مقدار (Ο(ξ(ω),x برای هر ξ موجه است.

در مسئله برنامه ریزی دو مرحله ای، مجموعه متغیرهای موجه، اشتراک بین X₁ و X₂ است، که شامل متغیرهای موجه مرحله اول است که در مرحله دوم نیز صدق می کند. مقدار تابع هدف نیز از جمع هزینه تصمیمات مرحله اول (c^Tx) و هزینه تصمیمات مرحله دوم ((Φ(x) به دست می آید. در مسئله برنامه ریزی احتمالی با بازگشت کامل و غیر کامل برای اشتراک بین این دو مجموعه داریم:

1 – اشتراک دو مجموعه X₁ و X₂ در X₁∩X₂ = X₁، مسائل با بازگشت کامل است.

2 – اشتراک دو مجموعه X₁ و X₂ در X₁∩X₂ ⊂ X₁، مسائل با بازگشت کامل است.

بنابراین، برنامه معادل قطعی رابطه (1) با فرض گسسته بودن متغیر تصادفی، به دو صورت زیر قابل بازنویسی است:

روش اول:

در این رابطه فرض می کنیم، ξ گسسته و تابعی از s در نظر گرفته می شود؛ s=1,2,…,S مجموعه متناهی از سناریوهای ممکن است، به طوری که هر سناریو بیانگر حالتی از پارامترهای تصادفی است؛ احتمال وقوع s امین ξ برابر با p_s در نظر گرفته می شود .

این فرم از مدل به دلیل سادگی آن، در تشریح الگوریتم های حل مسائل باز گشتی مکرر مانند الگوریتم تجزیه بندرز استفاده خواهد شد.

قضیه ۲: برای یک ξ معین، تابع مقدار (Ο(ξ(ω),x:

1 – یک تابع محدب خطی تکه ای بر حسب (h,T) است.

2 – یک تابع محدب خطی تکه ای بر حسب (q) است.

3 – یک تابع محدب خطی تکه ای در x برای x ∈ X₂ همه است.

4 – وقتی ξ یک متغیر تصادفی گسسته متناهی باشد، (Ο(ξ(ω),x بر روی X₂ ، محدود و خطی تکه ای خواهد بود.

برای روشن شدن مباحث بیان شده تا به حال، به حل مسئله کلاسیک کشاورز می پردازیم.

مثال 2: مسئله کشاورز

ادامه دارد…