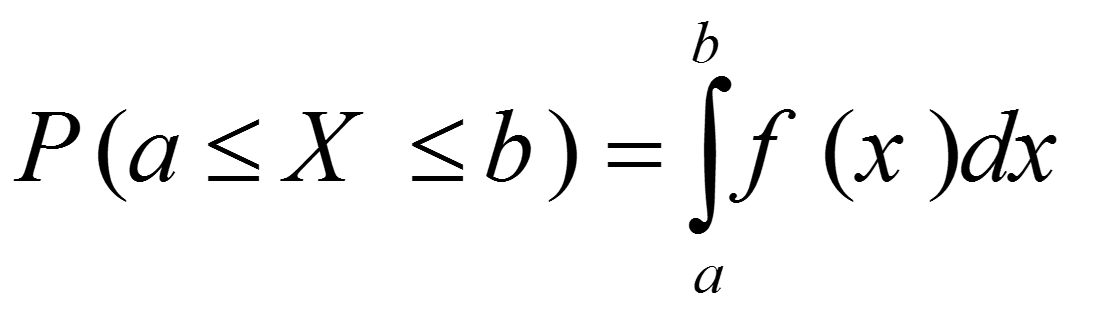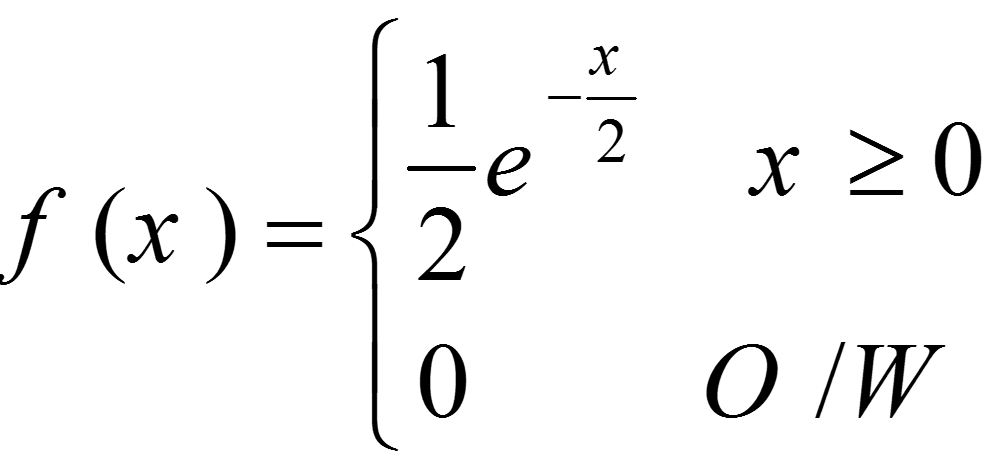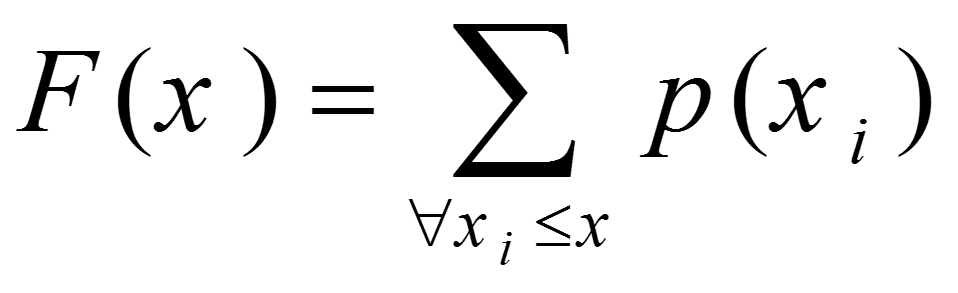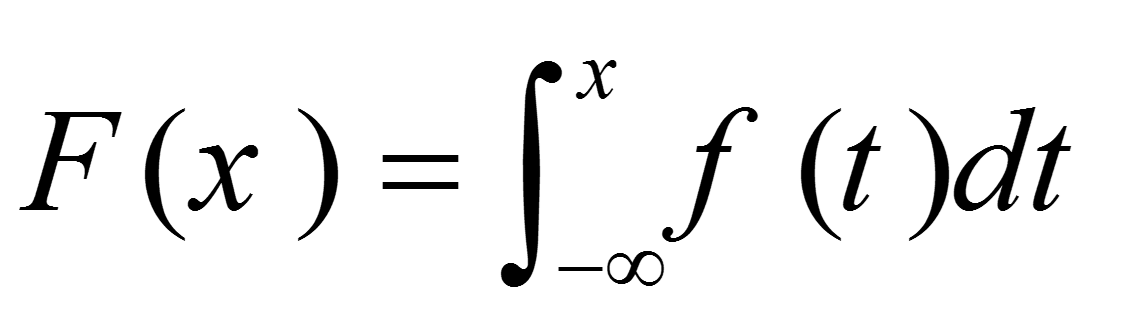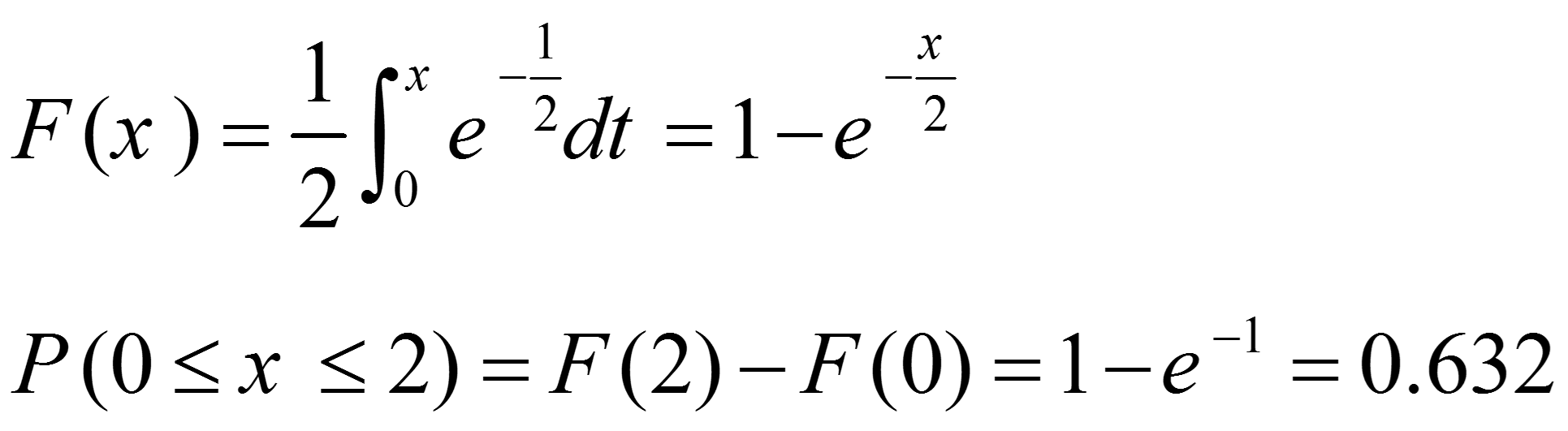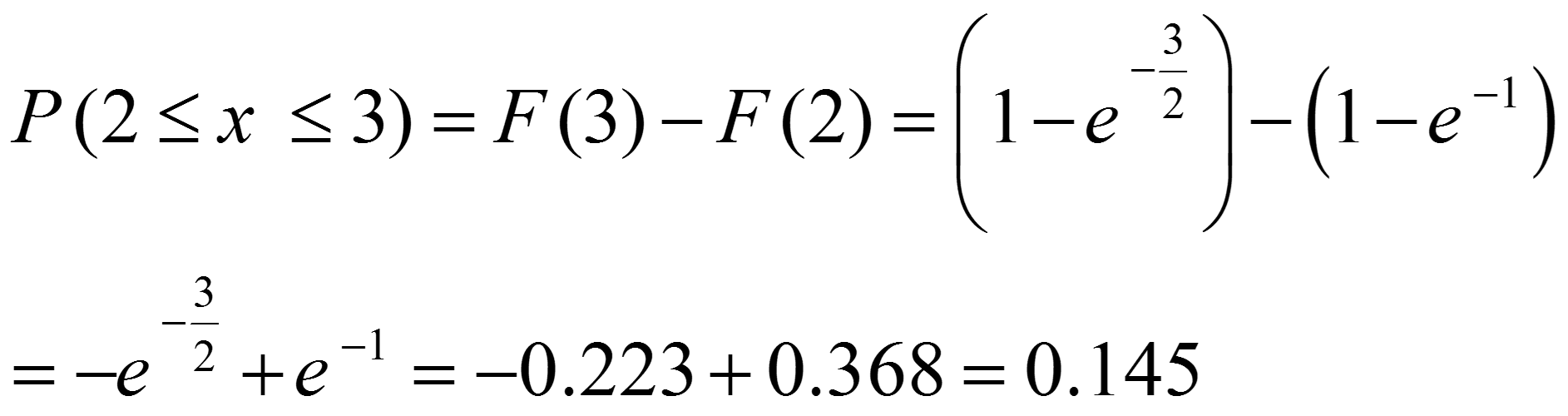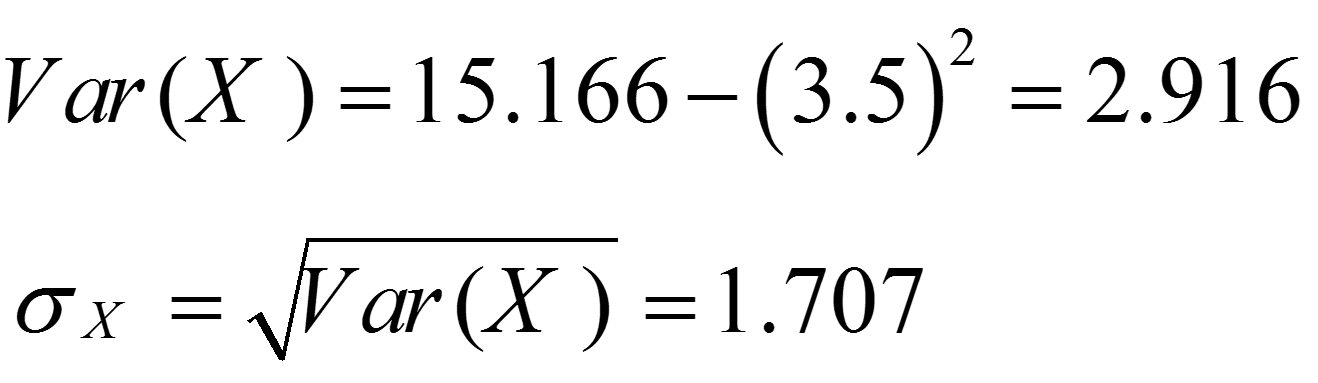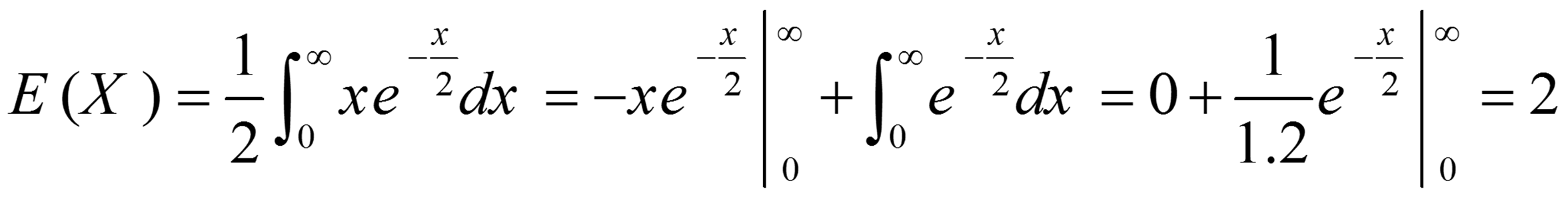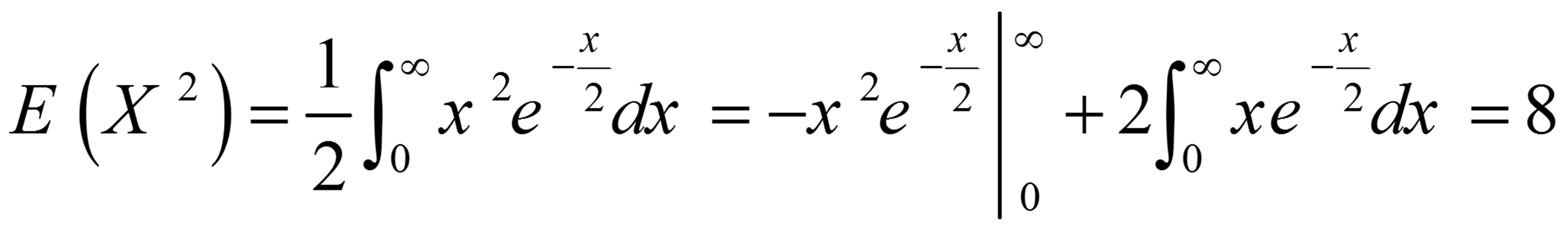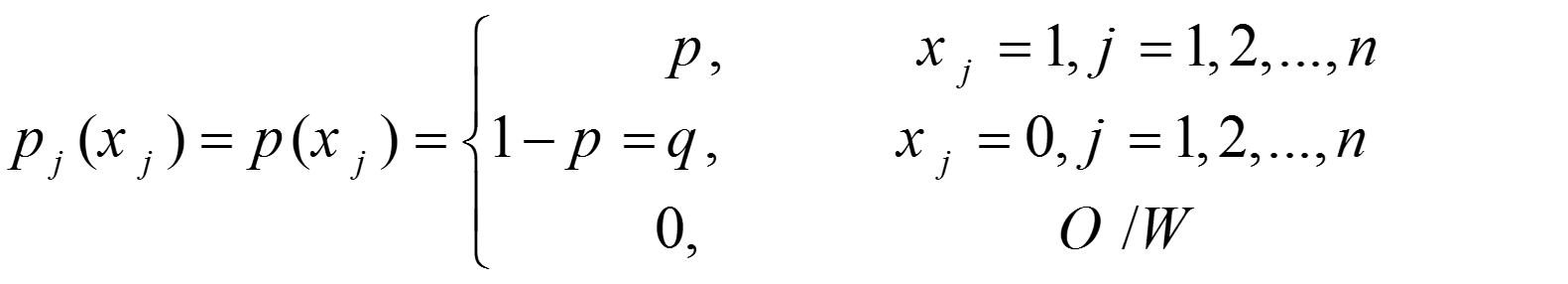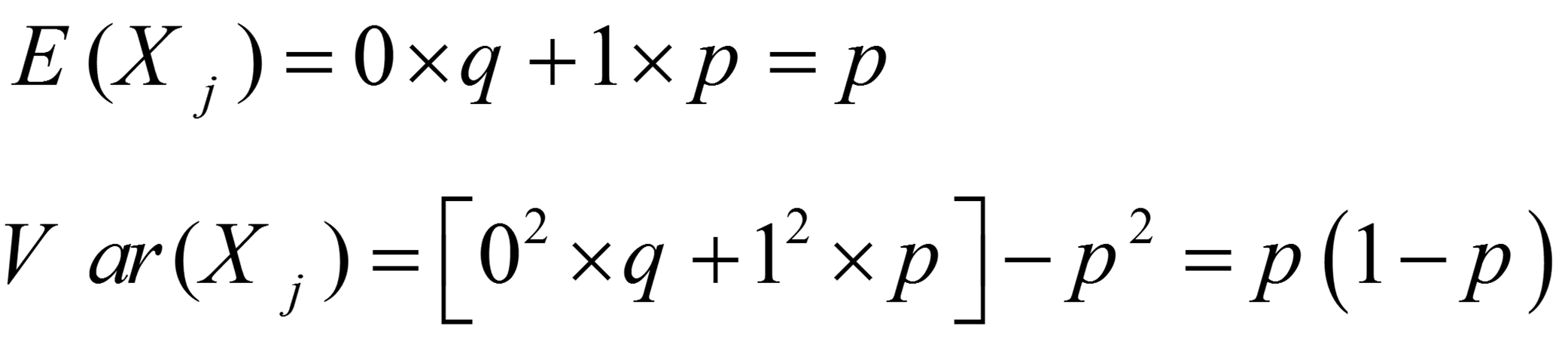درس 23: مدل‌های آماری

تهیه شده توسط گروه بهینه یاب

مقدمه

آموزش مدل های آماری

در مدلسازی پدیده‌های واقعی، کمتر وضعیت‌هایی وجود دارد که عملکرد نهادهای (Attribute) درون سیستم تحت بررسی را بتوان کاملا از قبل پیش بینی کرد و دنیایی که سازنده مدل می بیند احتمالی است و نه قطعی. مدل ساز می پندارد که این تغییرات به طور اتفاقی رخ می‌دهد و نمی‌توان آن را پیش بینی کرد. اما برخی مدل‌های آماری به خوبی از عهده تعیین مقدار نهادهای سیستم بر می آیند.

از طریق نمونه گیری از پدیده مورد علاقه می‌توان مدل آماری مناسبی بدست آورد. سپس مدل ساز شکل توزیع معینی را به صورت حدسی بر می‌گزیند. برآوردی از پارامتر(های) این توزیع حدس زده شده بدست می‌آورد و سپس برای بررسی میزان دقت در برازش پارامترها آزمون هایی انجام می‌شود که در درس های آینده نحوه این بررسی آموزش داده می‌شود.

آموزش مدل های آماری

مروری بر واژه ها و مفاهیم

متغیرهای تصادفی گسسته

X را متغیری تصادفی بگیرید. اگر تعداد مقادیر ممکن برای X متناهی یا نامتناهی شمارا باشد،X را متغیر تصادفی گسسته می نامیم. مقادیر ممکن X را می‌توان به صورت x₂، x₁، … فهرست کرد. در مورد متناهی بودن، تعداد مقادیر X فهرست پایان می‌گیرد. در مورد نامتناهی شمارا بودن آن‌ها، فهرست به گونه ای نامتناهی ادامه می یابد.

مثال: تعداد سفارش‌هایی که هر هفته به کارگاهی وارد می‌شود، مورد مشاهده قرار می‌گیرد. متغیر تصادفی مورد نظر X است، که داریم:

کلیه مقادیر ممکن X را فضای دامنه X، که R_X معرف آن است، مشخص می‌‌کند. در این جا داریم:

فرض کنید X متغیر تصادفی گسسته ای باشد. با هر نتیجه ممکن x_i در R_X، عدد p(x_i)=P(X=x_i) احتمال اینکه متغیر تصادفی مساوی x_i شود را تعیین می‌کند. اعداد p(x_i) برای i=1,2,3,… باید دو شرط زیر را داشته باشد.

1- به ازای همه مقادیر i داشته باشیم

2- داشته باشیم:آموزش مدل های آماری

حالت جمع شده زوج‌های ((x_i , p(x_i) را توزیع احتمال X و (p(x_i را تابع جرم احتمال متغیر تصادفی X می نامیم. آموزش مدل های آماری

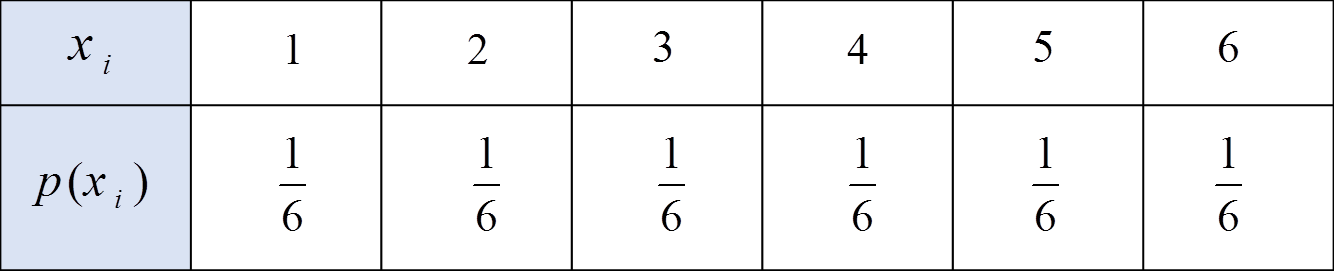
مثال: تجربه انداختن یک تاس را در نظر بگیرید. پس از آن که تاس انداخته شد، X را برابر با تعداد نقطه‌های وجه بالایی آن تعریف می‌کنیم. پس{R_X={1,2,3,4,5,6 . تابع توزیع احتمال گسسته این متغیر تصادفی X به صورت زیر است.

متغیر تصادفی پیوسته

اگر فضای دامنه متغیر تصادفی X فاصله یا مجموعه ای از فواصل باشد، Xرا متغیر تصادفی پیوسته می‌نامند. در مورد متغیر تصادفی پیوسته ای مانند X ، احتمال قرارگرفتن X در فاصله [a,b] به صورت زیر ارایه می‌شود.

تابع (f(x را تابع چگالی احتمال یا Probability density function یا به اختصار PDF متغیر تصادفی X می نامیم. در مورد PDF شرایط زیر صدق می‌کند.

الف) به ازای همه مقادیر x در R_X داریم

ب)

ج) اگر x در R_X نباشد، داریم:

نکته: روابط زیر براساس شرایط بالا برقرار است:

مثال: یک لامپ اشعه کاتدی که به منظور بازرسی ترک‌های بال‌های هواپیما به کار برده می‌شود و با متغیر تصادفی پیوسته ای چون X که همه مقادیر موجود در دامنه است معرفی می‌شود. PDF عمر لامپ بر حسب سال به شرح زیر است:

احتمال این که عمر لامپ اشعه کاتدی بین 2 و 3 سال باشد طبق رابطه زیر بدست می آید.

تابع توزیع تجمعی

تابع توزیع تجمعی یا Cumulative distribution function یا CDF که با نماد (F(x نشان داده می‌شود و این احتمال را اندازه گیری می‌کند که متغیر تصادفی X مقدار کمتر یا مساوی x بگیرید. به عبارت دیگر داریم:

اگر X گسسته باشد، داریم:

اگر X پیوسته باشد داریم:

برخی از ویژگی‌های CDF به صورت زیر است:

الف) F تابعی غیرنزولی است. اگر b>a باشد، آنگاه داریم:

ب)

ج)

از جمله پرسش‌هایی که در مورد X با استفاده از CDF پاسخ داده می‌شود می‌توان به احتمال وقوع x در بازه بین a و b به صورت زیر اشاره کرد:

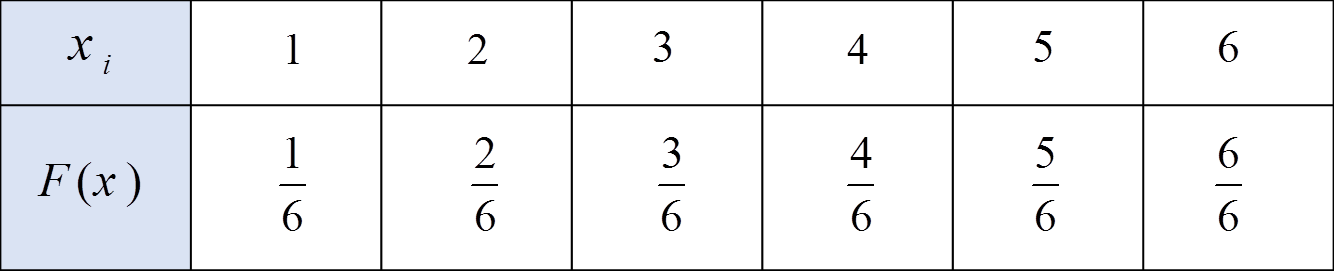
مثال: مثال پرتاب تاس عادل را در نظر بگیرید. تابع توزیع تجمعی و نمودار آن را رسم کنید.

جدول تابع توزیع احتمال تجمعی

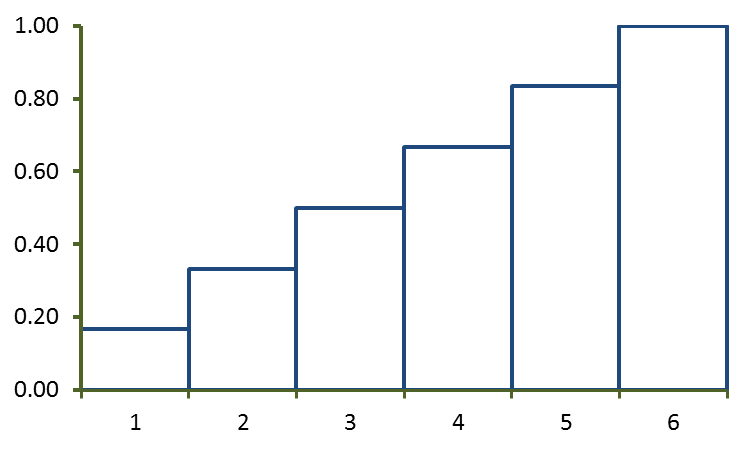
نمودار تابع توزیع احتمال تجمعی

مثال: لامپ اشعه کاتدی مثال متغیرهای تصادفی پیوسته را در نظر بگیرید. احتمال این که لامپ اشعه کاتدی کمتر از دو سال دوام بیاورد به شرح زیر تعیین می‌شود.

احتمال این که عمر لامپ اشعه کاتدی بین 2 تا 3 سال باشد طبق رابطه زیر محاسبه می‌شود.

امید ریاضی

از مفاهیم مهم در نظریه احتمال، مفهوم امید ریاضی متغیر تصادفی است. اگر X متغیر تصادفی باشد، امید ریاضی X را با نماد (E(X معرفی می‌شود و برای متغیرهای گسسته و پیوسته به شرح زیر تعریف می‌شود.

1 – اگر X گسسته باشد:

1 – اگر X پیوسته باشد:

نکته: امید ریاضی،(E(X، متغیر تصادفی X را میانگین یا گشتاور اول X نیز می نامند.

نکته: واریانس متغیر تصادفی X که با (Var(X معرفی می‌شود، به شرح زیر تعریف می‌شود.

مثال: میانگین و واریانس تجربه پرتاب تاس عادل را بدست آورید.

برای محاسبه (Var(X به صورت زیر عمل می‌کنیم.

بنابراین واریانس به صورت زیر محاسبه می‌شود.

مثال: میانگین و انحراف معیار لامپ اشعه کاتدی تشریح شده در مثال قبلی را بدست آورید.

به منظور محاسبه انحراف معیار به صورت زیر عمل می‌کنیم:

بنابراین:

وآموزش مدل های آماری

با میانگین عمر 2 سال و انحراف معیار 2 سال، به این نتیجه می‌توان رسید که عمر واقعی تغییر پذیری زیادی دارد.آموزش مدل های آماری

تابع توزیع‌های گسسته

آموزش مدل های آماری

متغیرهای تصادفی گسسته به منظور تشریح پدیده‌های تصادفی که در آن‌ها تنها مقادیر صحیح رخ می‌دهد به کار می رود. در ادامه چهار نوع توزیع را تشریح می‌کنیم.

توزیع برنولی

آموزش مدل های آماری

تجربه ای متشکل از n آزمایش را در نظر بگیرید که حاصل هر آزمایش موفقیت یا شکست است. اگر j امین آزمایش به موفقیت بیانجامد X_j=1 و اگر j-ام آزمایش به شکست بیانجامد X_j=0. n آزمایش برنولی را فرایند برنولی می نامند اگر آزمایش‌های مستقل از یک دیگر باشند؛ هر آزمایش تنها دو نتیجه ممکن (موفقیت یا شکست) داشته باشد؛ و احتمال موفقیت از یک آزمایش به آزمایش دیگر ثابت بماند. بنابر موارد گفته شده داریم:آموزش مدل های آماری

و

به توزیع فوق، توزیع برنولی می‌گویند.

همچنین میانگین و واریانس X_j را به شرح زیر محاسبه می‌کنیم.آموزش مدل های آماری

مه ریز غیرخطی و ارایه دستورهای ح