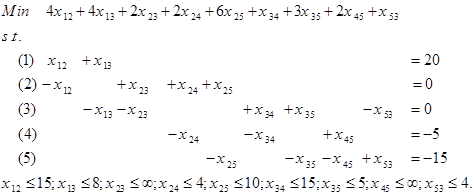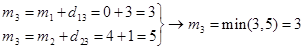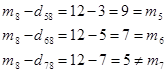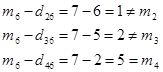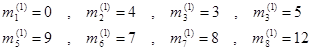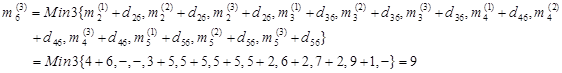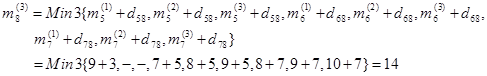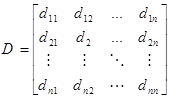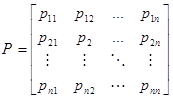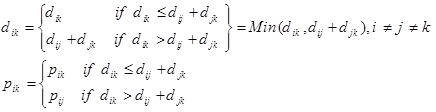مسئله کوتاهترین مسیر
برای دانلود خلاصه آموزش روش کوتاهترین مسیر لطفا ایمیل خود را وارد کنید تا این آموزش برای شما ارسال شود. این آموزش شامل فیلم، جزوه، پادکست و فایل ارایه است.
درس 6: مسئله کوتاهترین مسیر
تهیه شده توسط گروه بهینه یاب
تا کنون به بررسی مسئله برنامه ریزی خطی به صورت کلی پرداختیم. در این بخش به بررسی انواع خاص مسئله برنامه ریزی خطی خواهیم پرداخت. در این بخش ابتدا به بررسی مدل عمومی جریان در شبکه پرداختیم. سپس به بررسی مدل های خاص جریان در شبکه مانند مسئله حمل و نقل، مسیر بحرانی، مسئله جریان بیشین و مسئله کوتاهترین مسیر خواهیم پرداخت.
مسئله عمومی جریان در شبکه
در مسئله جریان در شبکه، به دنبال توزیع محصول همگن از کارخانه (مبادی) به بازار فروش (مقاصد) هستیم. فرض کنید تعداد کل واحدهای محصول تولید شده در هر کارخانه و تعداد کل محصول مورد نیاز معلوم است. همچنین لازم نیست که محصول مستقیما به مقاصد ارسال شود بلکه امکان دارد که از طریق سایر نقاط به مراکز توزیع ارسال شود. به علاوه، قیدهای ظرفیت بعضی از خطوط حملونقل را محدود میکند. هدف در این مسئله کمینه کردن هزینه حمل محصولها است.
مثال عددی از مسئله جریان در شبکه در شکل زیر را در نظر بگیرید. گرهها با دایره های شماره دار و کمانها با کمانها نشان داده شده اند. کمانها جهت دار هستند. مثلا مواد میتوانند از گره 1 به گره 2 فرستاده شود ولی از گره 2 به گره 1 این امکان وجود ندارد. کمان از گره i به گره j را به صورت i-j نشان میدهیم.
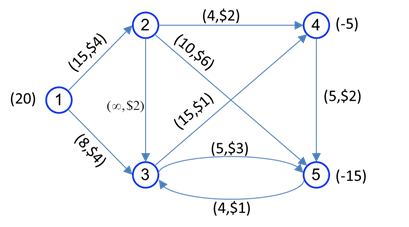
در مسئله جریان در شبکه، هدف یافتن الگوی جریان با هزینه کمینه است. برای تبدیل مسئله به صورت برنامهریزی خطی، فرض کنید:
xij : تعداد واحدهای حمل شده از گره i به گره j با استفاده از کمان i-j است.
مدل برنامهریزی خطی جریان در شبکه به صورت زیر ارایه میشود.
معادلات 1 تا 5، معادلات توازن جریان در شبکه است. برای مثال معادله جریان تعادل در گره 1 به صورت زیر میشود.
معادله فوق این نکته را بیان میکند که جریان خروجی از گره 1 ( x12+x13 )، باید برابر با میزان عرضه گره 1 (20) باشد. معادله توازن در گره 2، بیان میکند که جریان ورودی به گره 2 ( x12 ) برابر جریان خروجی از گره 2 ( x24+x25+x23) است.
مدل جریان در شبکه دارای ساختار خاصی است که برای ارایه دستور حل از آن مورد استفاده قرار میگیرد. متغیرهای جریان xij در معادلات توازن فقط ضریب 0، 1+ و 1- اخذ میکنند. به علاوه دقیقا در دو معادله توازن ظاهر میشوند: یک بار با ضریب 1+ مربوط به گرهای که از آن سرچشمه میگیرند و 1- مربوطه به گرهای که به آن وارد میشوند. با توجه به موارد فوق، فرم عمومی مسئله کمترین جریان در شبکه را به n گره به صورت زیر بیان میشود.
مدل فوق، مدل عمومی مسئله جریان کمینه در شبکه است. برای شرایط خاص، مدل فوق قابل تبدیل به فرم های ساده تری است که در ادامه برخی از این مدل های خاص را بیان میکنیم.
مسئله کوتاهترین مسیر در شبکه
یکی از کاربردهای عملی تئوری شبکهها در حل مسائل موجود در دنیای واقع مربوط به حل مسئله کوتاهترین مسیر در شبکه است. در این مبحث شبکههایی مورد بررسی قرار میگیرند که گرههای آن به مثابه نقاط مختلف موجود در یک منطقه و شاخهها نقش مسیرهای ارتباطی بین این نقاط را ایفا میکنند. هر نقطه (گره) از این شبکه به عنوان مبدا حرکت و هر نقطه (گره) دیگر به عنوان مقصد میتواند در نظر گرفته شود. هدف، تعیین مسیری بین مبدا و مقصد حرکت است که اگر این مسیر برای حرکت انتخاب شود، کمترین فاصله طی میشود که به آن مسئله کوتاهترین مسیر در شبکه گفته میشود.
شبکههایی که در رابطه با این مطلب مطرح میشوند، از لحاظی به دو نوع تقسیم میشوند:
- شبکههای بدون حلقه
- شبکههای دارای حلقه
در ادامه هر یک از این دو نوع شبکه را در مسئله کوتاهترین مسیر مورد بررسی قرار میدهیم.
شبکههای بدون حلقه
این شبکهها اغلب شبیه به شبکههای برداری ساده هستند، اما در این جا هر دو گرهای میتوانند به عنوان گرههای مبدا و مقصد حرکت در نظر گرفته شوند. برای حل مسئله کوتاهترین مسیر در این شبکهها معمولا روش ساده حسی بکار میرود.
روش ساده کوتاهترین مسیر
در این روش یک حرکت محاسباتی از گره مبدا(شروع) تا گره مقصد(پایان) انجام میشود. در طی این حرکت محاسباتی، به هر گره یک کد (m) اختصاص مییابد که نشان دهنده کوتاهترین فاصله آن گره از گره شروع است. فرض بر این است که شماره گره شروع برابر با 1 و شماره گروه پایان معادل n در نظر گرفته شده و گرههای میانی نیز به ترتیب صعودی شماره گذاری شده اند. گامهای الگوریتم این روش به صورت زیر است:
گام 1: به گره شروع، کد برابر با صفر اختصاص دهید( m1 = 0 ).
گام 2: کد گره j همان mj را از رابطه زیر بدست آورید:
که در آن S مجموعه گرههایی است که شاخههای ورودی به گره j از آن گرهها خارج شده اند و dij فاصله مستقیم از گره i تا گره j است.
گام 3: هنگامیکه گره پایان کد گرفت ( mn )، این کد معرف کوتاهترین فاصله بین گروه شروع و پایان شبکه است.
گام 4: به منظور یافتن کوتاهترین مسیر، از روش حرکت برگشتی استفاده میشود. به بیان دیگر هر یک از شاخههای ورودی به یک گره که تعیین کننده کد آن گره است، بر روی کوتاهترین مسیر قرار دارد.
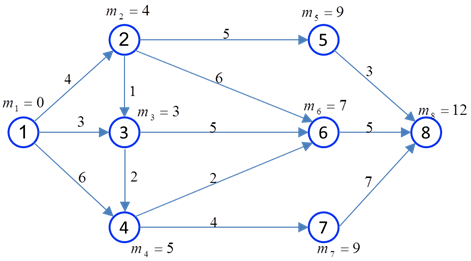
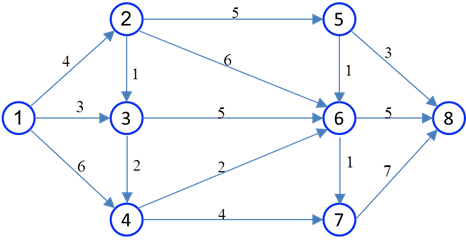
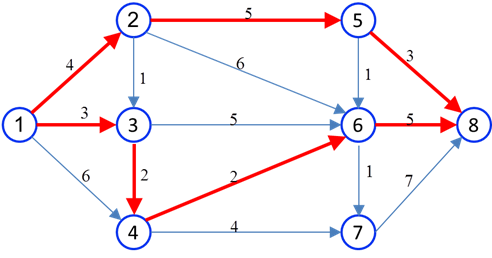
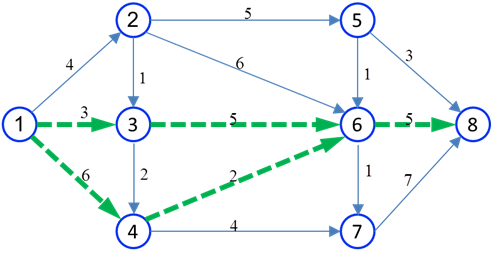
مثال: با استفاده از روش ساده حسی، کوتاهترین فاصله و مسیر بین گرههای 1 و 8 در شبکه شکل زیر را تعیین کنید. فاصله مستقیم بین هر دو گره مجاور بر روی شاخه متصل کننده آن دو درج شده است.
حل:
ابتدا کد گره 1 را برابر صفر در نظر گرفته میشود( m1 = 0 ).
برای گره 2 میتوان نوشت:
برای گره 3 چون دو مسیر برای رسیدن به این گره وجود دارد بایستی حداقل این دو مسیر در نظر گرفته شود:
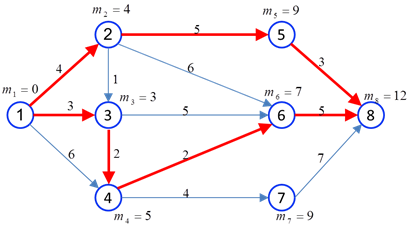
محاسبات برای سایر گرهها نیز به همین ترتیب انجام میشود که نتایج آن در شکل زیر خلاصه شده است. ملاحظه میشود کوتاهترین فاصله گره 8 از گره 1 برابر با 12 واحد است.
برای تعیین کوتاهترین مسیر بین گرههای 1 و 8 از حرکت برگشت استفاده میشود. در این حرکت هر گرهای (j) که کد آن ( ) در رابطه زیر صدق کند
آنگاه بر روی کوتاهترین مسیر واقع است. حرکت از گره پایان آغاز میشود، سه شاخه به این گره وارد شده است:
کمانها (5,8) و (6,8) بر روی کوتاهترین مسیر قرار دارد. بنابرین تا کنون دو فقره کوتاهترین مسیر وجود دارد. ابتدا کار از گره 5 ادامه میدهیم.
کمان (2,5) بر کوتاهترین مسیر واقع است.
کمان (1,2) بر کوتاهترین مسیر واقع است.
مسیر یکم مشخص شد. اکنون نوبت به مسیر دوم است. کار را از گره ششم ادامه میدهیم.
کمان (4,6) بر کوتاهترین مسیر قرار دارد.
کمان (3,4) بر کوتاهترین مسیر واقع است.
کمان (1,3) بر کوتاهترین مسیر واقع است.
ملاحظه میشود در این شبکه، دو مسیر وجود دارد که کوتاهترین مسیر را دارد.
چندمین (k-امین) کوتاهترین مسیر
راننده یک اتوبوس مسافربری برای رساندن مسافرین خود از شهر مبدا (X) به شهر مقصد (Z) کوتاهترین مسیر را انتخاب کرده است که در طی آن از شهرهای U،V و W عبور میکند. فرض کنید در یک هفته خاص، برای رفتن به شهر U مانعی وجود دارد، بنابراین راننده اتوبوس در نظر دارد از دومین کوتاهترین مسیر استفاده کند. این مثال نشان میدهد که گاهی اوقات لازم است که دومین، سومین یا به طور عمومی k امین کوتاهترین مسیر تعیین شد. برای تعیین k-امین مسیر کوتاه، تغییری به صورت زیر در گام دوم روش ساده کوتاهترین مسیر ایجاد میشود.
که در آن منظور از Mink انتخاب k-امین مقدار حداقل در داخل {} است.
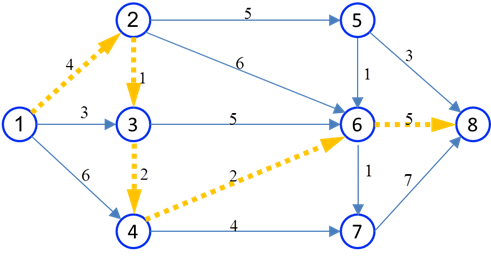
مثال: یکمین، دومین، سومین مسیر کوتاه بین گرههای 1 و 8 را در شبکه زیر تعیین کنید.
حل: چنانچه به روش ساده کوتاهترین فاصله عمل شود، کوتاهترین فاصله (یکمین فاصله کوتاه) تا هر گره بدست میآید:
در خصوص دومین فاصله کوتاه، برای گره مبدا همچنان کد برابر با صفر اختصاص مییابد.
فقط یک شاخه به گره 2 وارد میشود و بنابراین دومین فاصله کوتاه بین گرههای 1 و 2 وجود ندارد:
اما برای گره 3 میتوان نوشت:
برای سایر گرهها به صورت زیر عمل میکنیم:
سومین فاصله کوتاه از گره مبدا تا خودش نیز برابر با صفر است:
چون فقط یک شاخه به گره 2 وارد میشود، بنابراین سومین فاصله کوتاه بین گرههای 1 و 2 نیز وجود ندارد.
در مورد گره 3 داریم:
به همین ترتیب میتوان نوشت:
دومین و سومین مسیر کوتاه بین گرههای 1 تا 8 با استفاده حرکت برگشت تعیین میشود. برای دومین مسیر کوتاه دو جواب و برای سومین مسیر کوتاه یک جواب وجود دارد.
دومین کوتاهترین مسیر
سومین کوتاهترین مسیر
در شکلهای زیر سه نوع مسیر نمایش داده شده است:
کوتاهترین مسیرها
دومین کوتاهترین مسیر
سومین کوتاهترین مسیر
شبکههای دارای حلقه
در این شبکهها حلقه وجود دارد، به این معنی که بین تعدادی از گرهها یک کمان برای رفت و یک کمان دیگر برای برگشت وجود دارد. در این جا برای حل مسایل در شبکههای حلقه دار (مسئله کوتاهترین مسیر) دو روش بیان میشود:
روش کوتاهترین مسیر دایکسترا
روش دیکسترا Dijkestra به نام ابداع کننده آن موسوم است و در آن به هر گره دو کد اختصاص مییابد:
mi: کوتاهترین فاصله گره i از گره مبدا حرکت تا مرحله جاری الگوریتم که به آن کد موقت گفته میشود زیر ممکن است در مراحل بعدی، فاصله کوتاهترین نیز بدست آید.
Mi: کوتاهترین فاصله مطلق گره i از گره مبدا حرکت که کد دایم نام دارد زیر در مراحل بعدی نیز فاصله کوتاهتر از آن بدست نخواهد آمد.
الگوریتم دیکسترا به صورت زیر است:
گام 1: کد دایم برابر با صفر به گره شروع اختصاص دهید( M1 = 0 )
گام 2: به گرههای مجاور گرههایی که کد دایم گرفته اند، با استفاده از رابطه زیر کد موقت اختصاص دهید:
که در آن dij فاصله مستقیم از گره i با کد دایم تا گره j که بایستی به آن کد موقت اختصاص یابد، است.
چنانچه گرهای پیش از این کد موقت گرفته است، آن کد با کد موقت جدید مقایسه و کد کوچکتر برگزیده میشود. سپس از بین کلیه گرههایی که تاکنون کد موقت گرفته اند، گرهای که کوچکترین کد را دارد، آن کد را به کد دایم تبدیل کنید. اکنون به گرههای مجاور گرهای که کد دایم گرفته، کد موقت اختصاص و همین طور ادامه دهید.
گام 3: هنگامی که گره پایان (مقصد) کد دایم گرفت، متوقف شوید. Mn نشان دهنده کوتاهترین فاصله گره پایان از گره شروع است.
گام 4: به منظور یافتن مسیر بهینه در مسئله کوتاهترین مسیر، از روش حرکت برگشت با رابطه زیر استفاده کنید:
روش جامع مسئله کوتاهترین مسیر
روش دیکسترا روش آسانی برای تعیین کوتاهترین مسیر در مسئله کوتاهترین مسیر در شبکه است، اما ضعف روش در این است که با هر بار اجرای الگوریتم، فقط کوتاهترین فاصله بین دو گره مبدا و مقصد مشخص میشود. اما با اجرای الگوریتم روش جامع کوتاهترین مسیر، کوتاهترین فاصله و مسیر بین کلیه گرهها از یکدیگر قابل محاسبه است.
فرض کنید در شبکه مورد نظر n گره داشته باشد. گره شروع با شماره 1 و گره پایان با شماره n مشخص و سایر گرهها نیز به ترتیب صعودی از گره شروع تا پایان شماره گذاری میشوند. در این روش دو ماتریس فاصله (D) و مسیر (P) تعریف میشود. dij نشان دهنده فاصله گره i از گره j و pij مسیر رسیدن از گره i به گره j است. هر گاه مسیر مستقیمی برای رسیدن از یک گره به گره دیگر وجود نداشته باشد، فاصله بین آنها ∞ در نظر گرفته میشود و مسیر بین آنها نیز با علامت تیره “-” مشخص خواهد شد. لازم به ذکر است ممکن است فاصله رفت از یک گره به گره دیگر یعنی dij با فاصله برگشت یعنی dji یکی نباشد.
به عنوان مثال d12 فاصله گره 1 تا 2 است.
به عنوان مثال، p12 مسیر رسیدن از گره 1 به گره 2 است.
در مرحله j-ام (j=1,2,3,…,n)، گره j به عنوان واسط در نظر گرفته میشود و فاصله و مسیر رسیدن بین هر دو گره غیر از گره j با استفاده از این واسطه بدست میآید. اگر این فاصله از فاصله قبلی کمتر باشد، جایگزین آن میشود و در غیر این صورت فاصله قبلی همچنان حفظ میشود. به بیان دیگر، ماتریس های مرحله j-1 یعنی Dj-1 و Pj-1 توسط روابط زیر به ماتریس های مرحله j یعنی Dj و Pj تبدیل خواهند شد.
.