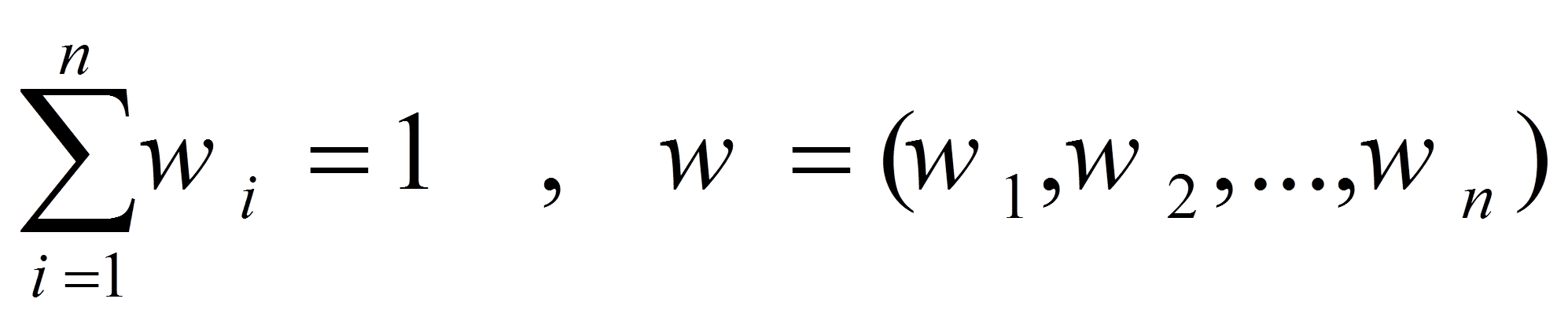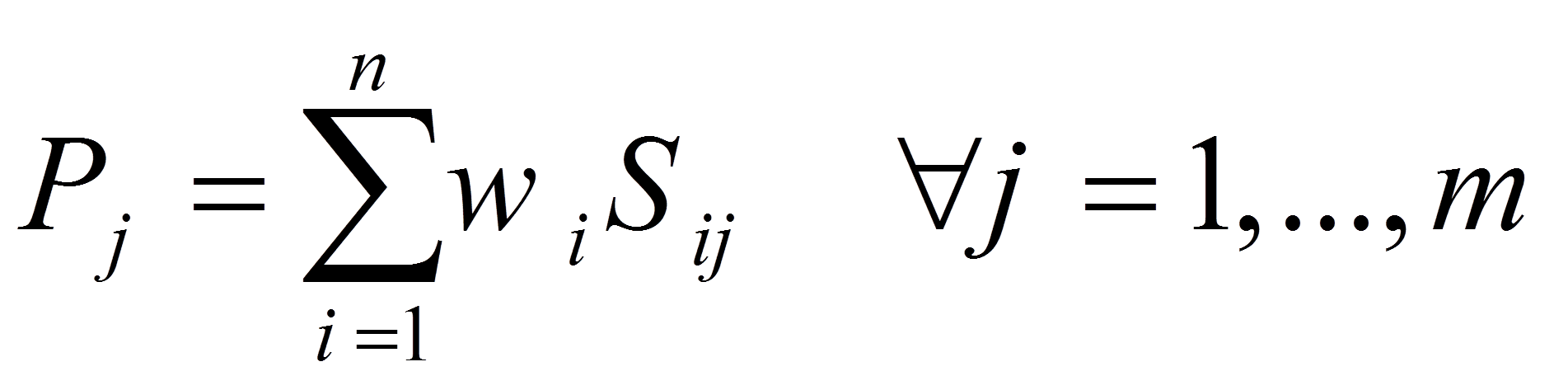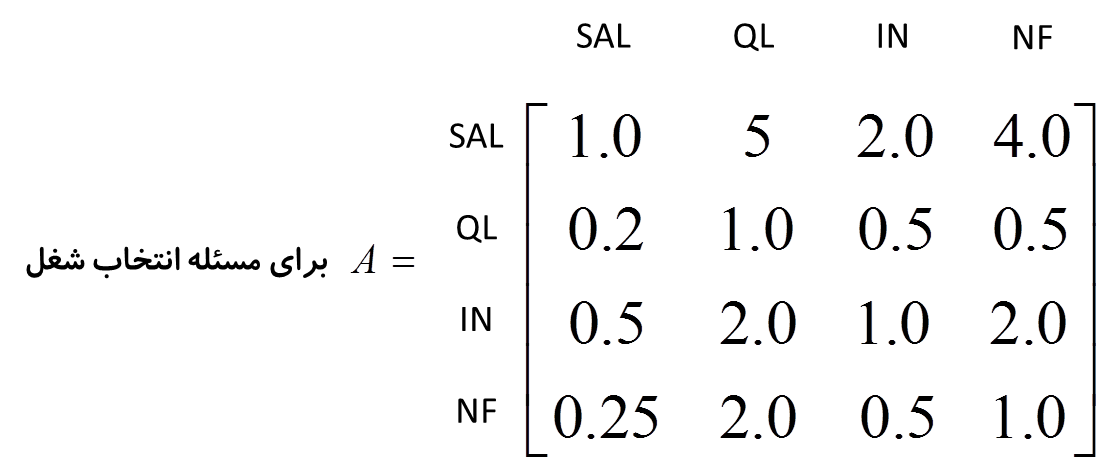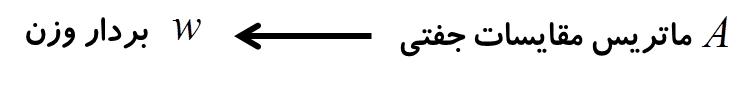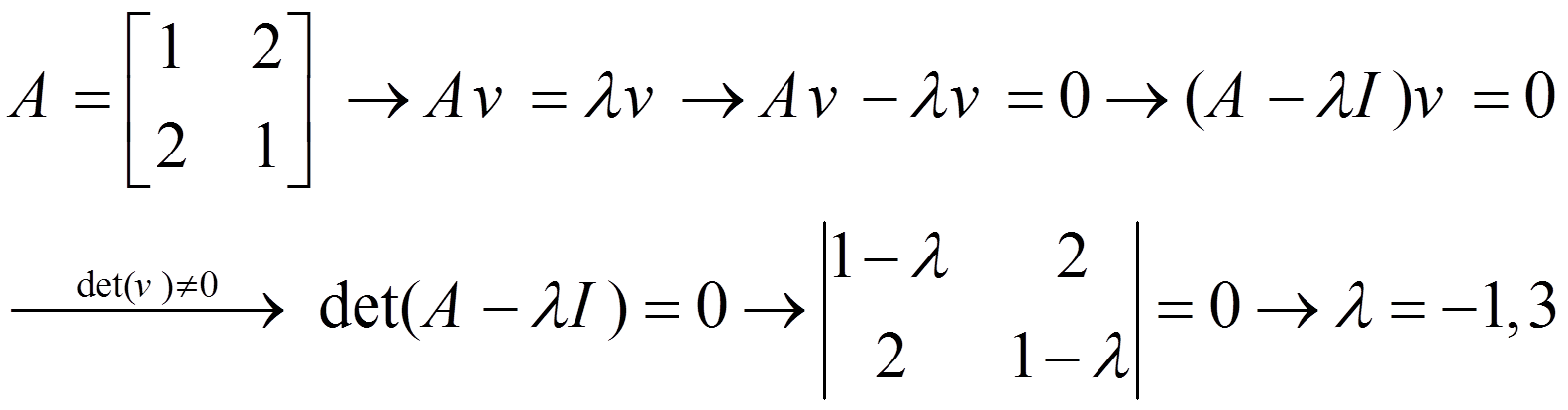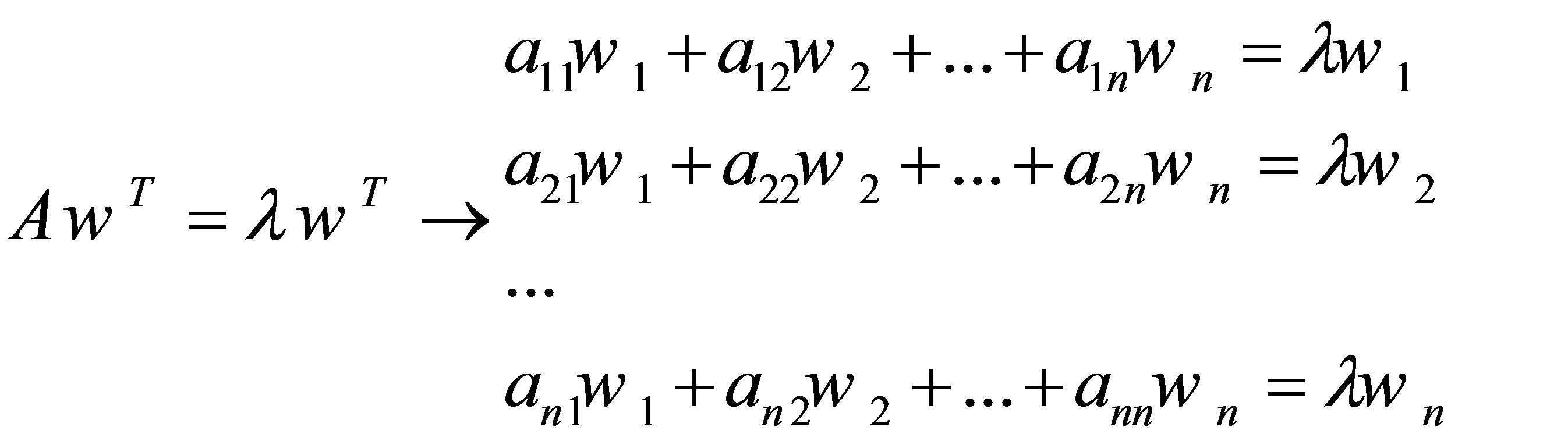درس 20: فرآیند تحلیل سلسله مراتبی یا AHP

تهیه شده توسط گروه بهینه یاب

مقدمه

روش تحلیل سلسله مراتبی یا AHP یا Analytical Hierarchy Process یک روش تصمیم گیری چند معیاره یا Multiple-criteria decision-making یا MCDM است. این روش توسط آقای توماس ساعتی (Thomas Saaty) در دهه هشتاد میلادی ابداع شد. در این روش قضاوت افراد خبره در مورد مساله مورد بحث خواهد گرفت.

خلاصه گام‌های حل یک مسئله تصمیم گیری چند معیار با استفاده از روش AHP به صورت زیر است:

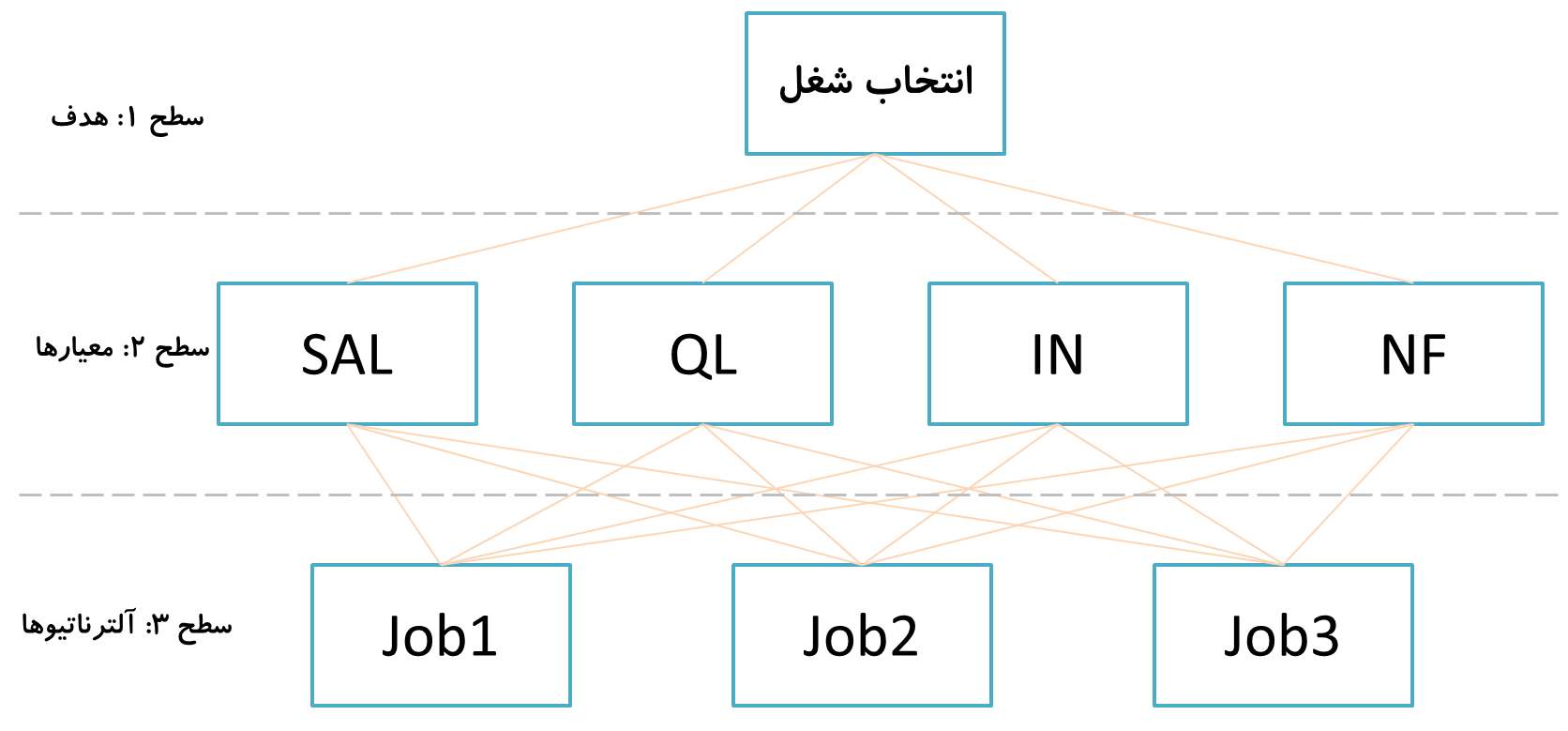
گام 1) تعریف به صورت سلسله مراتب درختی: در این گام مسئله به صورت یک سلسله مراتب چند سطحی تعریف می‌شود: در سطح 1 هدف مساله، در سطح 2 معیارها و در سطح 3، آلترناتیوها یا گزینه‌ها تشکیل می‌دهند. هر یک از عناصر موجود در این سلسله مراتب به صورت گره نمایش داده می‌شود و ارتباط ما بین عنصرهای یک سطح و سطح دیگر از طریق یال مشخص می‌شود. بین عناصر در یک سطح یال موجود نیست. البته هر سطح اصلی می‌تواند دارای زیر سطح فرعی نیز باشد. برای روشن شدن موضوع یک مثال می‌زنیم.

مثال انتخاب یک شغل

فرض کنید که جهت انتخاب شغل آینده چهار معیار زیر در نظر است:

• میزان حقوق سالانه (SAL)
• محیط کاری (QL)
• علاقه مندی به شغل (IN)
• محل کار (NF)

با توجه به این معیارها می‌خواهیم از بین سه پیشنهاد شغلی Job1 ، Job2 و Job3 یکی را انتخاب کنیم. نمایش سلسله مراتبی این انتخاب به صورت زیر می‌شود:

گام 2) تعیین اهمیت هر معیار از دید تصمیم گیرنده یا فرد خبره: در این گام با استفاده از نظر تصمیم گیرنده یا تصمیم گیرندگان یا افراد خبره، اهمیت نسبی معیارهای نسبت به هم تعیین می‌شود و با استفاده از روش انتخاب وزن، وزن w_i معیار i –ام تخصیص می‌یابد. برای محاسبه وزن n معیار فرض می‌شود:

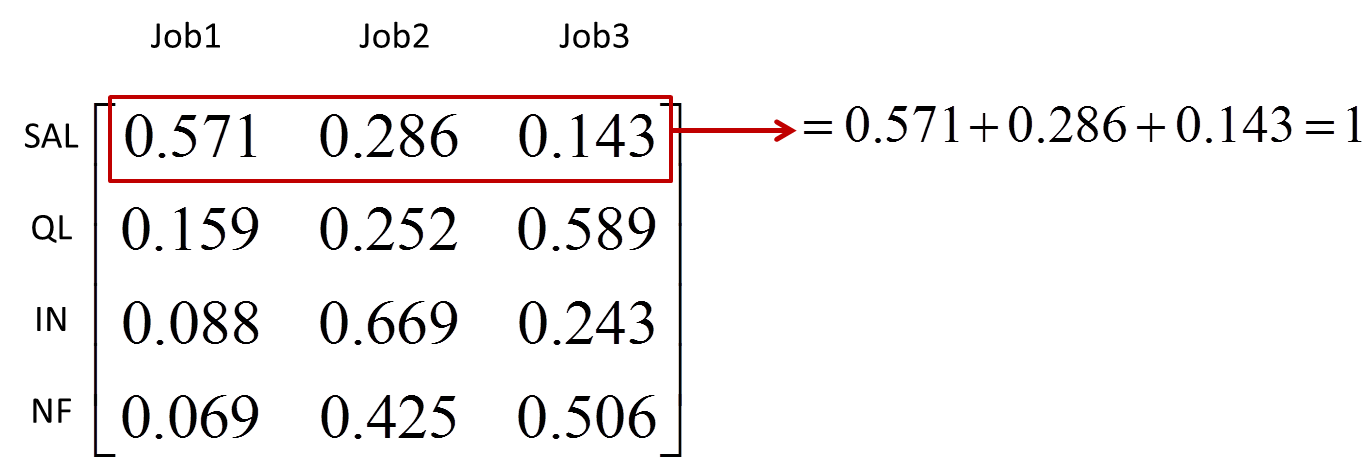
گام 3) تعیین امتیاز نسبی هر آلترناتیو با توجه به معیارها: در این گام امتیاز نسبی آلترناتیو j نسبت به معیار i بدست می آید که به صورت S_ij نمایش می‌دهیم و بیانگر علاقه نسبی به آلترناتیو i با توجه به معیار i است. محاسبه S_ij با استفاده از روش تخصیص امتیاز نسبی و با کمک اطلاعات ورودی از تصمیم گیرندگان انجام می‌شود. در این حالت نیز فرض می‌شود که:

گام 4: محاسبه امتیاز نهایی هر آلترناتیو: در این گام امتیاز نهایی هر آلترناتیو با استفاده از وزن نسبی هر معیار و امتیاز نسبی آلترناتیو j نسبت به تمامی معیارها به صورت محاسبه می‌شود:

گام 5: انتخاب بهترین آلترناتیو: آلترناتیو یا گزینه ای انتخاب می‌شود که عبارت زیر در آن برقرار باشد.

یکی از مهمترین مزایا روش AHP تعیین میزان ناسازگاری قضاوت‌های تصمیم گیرنده است. برای مثال اگر معیار A دو برابر B و معیار B سه برابر معیار C اهمیت داشته باشد، از دید یک فرد کاملا منطقی باید اهمیت معیار A نسبت به معیار C، شش برابر باشد. اما از دید انسان‌ها که کاملا منطقی نیستند ارزش گذاری اهمیت نسبی هر دو معیار نسبت به هم می‌تواند کاملا براساس نظر تصمیم گیرنده تعیین شود. با استفاده از روش AHP می توان میزان سازگاری تصمیم گیران را محاسبه کرد و در صورت ناسازگار بودن تصمیم گیر، وی را از فرایند انتخاب تصمیم نهایی حذف کرد.

در ادامه این جزوه، گام‌های اشاره شده در بالا با جزییات بیشتر بیان می‌شود.

روش انتخاب وزن هر معیار Assign weights to criteria

فرض کنید n معیار در مساله موجود است. ابتدا با نظر تصمیم گیرنده (یا افراد خبره ) ماتریس مقایسه جفتی (Pairwise Comparison Matrix) که همان A را تشکیل می‌دهیم که در آن هر عنصر a_ij بیانگر آن است که از دید تصمیم گیرنده چقدر معیار i –ام نسبت به معیار j-ام دارای اولویت است.

جهت انجام این مقایسه، از سیستم مقیاس عددی زیر استفاده می‌شود.

در هنگام تشکیل این ماتریس سه نکته زیر رعایت را باید مدنظر گرفت.

نکته 1: اگر معیار i ام k برابر معیار j –ام اهمیت داشته باشد معیار j-ام 1/k معیار i-ام اهمیت دارد. به این اصل، اصل وارانگی اتلاق می‌شود.

نکته 2: a_ii = 1

برای مثال می توانید در ماتریس مقایسه جفتی دو نکته فوق را مشاهده کرد.

نکته3: مرتبه یا رنک Rank این ماتریس برابر یک است.

در روش AHP، ابتدا باید ماتریس مقایسه‌های جفتی A که اولویت معیارها را نسبت به هم مشخص می‌کند تبدیل به بردار می‌شود که در حقیقت این بردار وزن هر معیار را مشخص می‌کند.

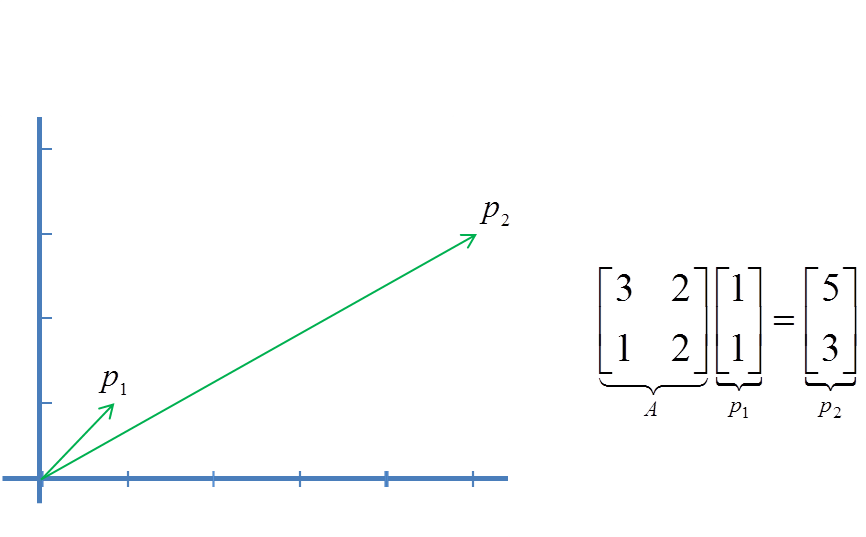
یک ماتریس در حقیقت یک تبدیل خطی یا Linear Transformation را می‌تواند بر روی یک بردار اعمال کند. برای مثال داریم:

بردار ویژه یا Eigen Vectors برداری است که وقتی تبدیل خطی بر روی آن اعمال شود فقط طول آن تغییر می‌کند و نه جهت آن.

مقدار ویژه یا Eigen Value در حقیقت اندازه این تغییر طول را مشخص می‌کند. برای مثال داریم:

جهت تبدیل ماتریس A به یک بردار وزنی از مفهوم بردار ویژه استفاده می‌کنیم.

که در آن، A ماتریس مقایسات جفتی، w^T بردار ویژه یا همان بردار وزنی و λ مقدار ویژه هستند.

در این سیستم معادلات w^T و λ مجهول هستند. فرم گسترده معادله فوق به صورت زیر می‌شود.

از طرف دیگر داریم:

و همچنین باید det(A-λI)=0 باشد که از روی آن λ تعیین می‌شود و سپس با حل دستگاه فوق w₁,w₂,…,w_n را بدست می آوریم. در عمل به دلیل وقت گیر بودن سعی می‌کنیم از روش‌های تخمینی که با دقت کافی این مقادیر را بدست می آورد استفاده کنیم.