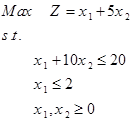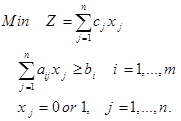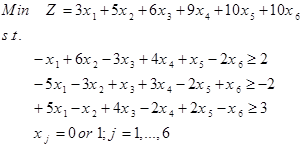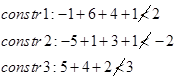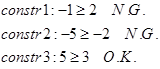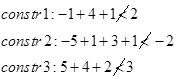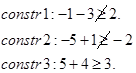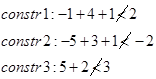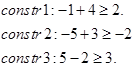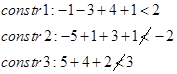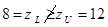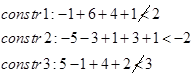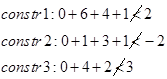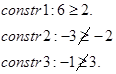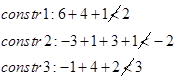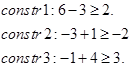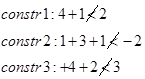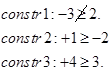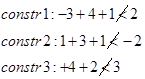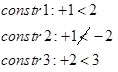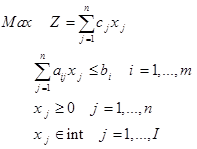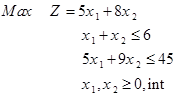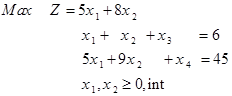حل مسائل برنامه ریزی عدد صحیح به روش شاخه و کرانه

درس 12: حل مسائل برنامه ریزی عدد صحیح به روش شاخه و کرانه

تهیه شده توسط گروه بهینه یاب

 

 

تفاوت اصلی یک مسئله برنامه‌ریزی عدد صحیح و برنامه‌ریزی خطی در فرض صحیح بودن متغیرهای مسئله است. شاید در نگاه اول صحیح بودن متغیرها باعث می‌شود که تعداد جواب‌های امکان پذیر شمارا باشد که با کنترل تمامی آن‌ها می‌توان جواب بهینه را یافت. فرض کنید یک مدل دارای n متغیر دودویی (مقدار صفر یا یک می‌تواند اخذ نماید) باشد. اگر n=10 باشد، تعداد جواب‌های بیش از 1000 تا و اگر n=20 باشد، تعداد جواب‌ها، بیش از یک میلیون و اگر n=30 باشد، تعداد جواب‌ها بیشتر از یک میلیارد خواهد بود که حتی سریعترین کامپیوترها قادر به شمارش تمامی جواب‌ها نخواهند بود. حال اگر تعداد متغیرها از مقیاس میلیون باشند، دشوار به سرعت است بیشتر می‌شود.

پیچیدگی محاسبات یک مسئله برنامه ریزی عدد صحیح به دو عامل بستگی دارد:

1 – تعداد متغیرهای عدد صحیح

2 – ساختار مسئله

همان طور که ملاحظه می‌شود تعداد محدودیت‌ها اثری در دشوار حل مسئله ندارد که این برخلاف مسئله برنامه‌ریزی خطی است. از آنجایی که حل مسائل برنامه ریزی عدد صحیح عملا بسیار دشوار تر از حل مسائل برنامه‌ریزی خطی است، لذا گاهی منطقی به نظر می‌رسد که با حذف محدودیت‌های عدد صحیح، مسئله را به مسئله برنامه ریزی خطی آزاد شده تبدیل ساخت و سپس آن را با روش سیمپلکس حل جواب‌ها را گرد کرد. این روش ممکن است برای حل برخی از مسائل کاربردی که مقدار بسیار بزرگی دارند مناسب باشد. ولی این روش دارای دو اشکال زیر است:

1- شاید جواب گرد شده دیگر موجه نباشد.

2- شاید جواب گره شده دیگر بهینه نباشد.

برای تشریح دو اشکال فوق، مثال زیر را در نظر بگیرید.

جواب بهینه مسئله فوق به صورت زیر می شود.حل مسائل برنامه ریزی عدد صحیح به روش شاخه و کرانه حل مسائل برنامه ریزی عدد صحیح به روش شاخه و کرانه

متغیری که غیر صحیح دارد یعنی x₂ را به عدد صحیح x₂=1 گرد می‌کنیم، جواب حاصل x₂=1 , x₁=1 و z=7 می‌شود که این جواب با جواب بهینه مدل اصلی، یعنی z=10، x₂=2,x₁=0 اختلاف زیادی دارد.

متداول ترین الگوریتم برای حل مسائل برنامه ریزی عدد صحیح، روش انشعاب و تحدید یا شاخه و کرانه (Branch and Bound) است که نکته اصلی در آن، شمارش ضمنی جواب‌های موجه است. در ادامه این روش مورد بررسی قرار می‌گیرد.

روش شاخه و کرانه Branch and Bound

چون تعداد جواب‌های موجه یک مسئله برنامه ریزی عدد صحیح محدود، متناهی است، لذا طبیعی است که برای پیدا کردن جواب بهینه آن از روش شمارش (Enumeration procedure) استفاده شود. همان طور که گفته شد، چون تعداد جواب‌ها بسیار زیاد است، هر روش شمارش باید به صورت آگاهانه طوری طراحی شود که درصد کمی ‌از جواب‌ها را مورد بررسی قرار دهد. در این بخش حل مسائل برنامه ریزی عدد صحیح به روش شاخه و کرانه بررسی می شود.

مبنای روش شاخه و کرانه برای حل مسائل برنامه ریزی عدد صحیح به شرح زیر است:

فرض کنید تابع هدف مسئله مورد نظر باید حداقل شود و مقدار تابع هدف نیز از مقدار مشخصی که آن را حد بالا (Upper Bound) (با z_U نشان داده می‌شود) تجاوز نمی‌کند. این حد بالا معمولا مقدار تابع هدف به ازای بهترین جواب موجهی است که تاکنون پیدا شده است. منطقه جواب به چند زیر مجموعه منشعب می‌شود. آنگاه حد پایین (Lower Bound) هر زیر مجموعه ( z_L ) بدست می‌آید. این حد پایین به این معنا است که z_L از z_U بیشتر باشد از بررسی خارج می‌شود. هر زیر مجموعه که جواب موجه ندارد و یا این که بهترین جواب موجه آن یافته شده است، از بررسی خارج می‌شود. هر زیر مجموعه‌ای که به هر کدام از دلایل فوق حذف شوند به ته رسیده یا fathomed گفته می‌شود.

وقتی یک مجموعه به ته می‌رسد، یکی دیگر از مجموعه‌های باقی مانده که مثلا بهترین حد را دارند انتخاب می‌شود. در عمل شاخه شدن بر روی آن انجام می‌شود. این کار تا زمانی ادامه می‌یابد که جواب موجهی بدست آید که مقدار تابع هدف آن از حد پایینی هیچکدام از زیر مجموعه‌های باقی مانده بیشتر نباشد و چنین جوابی، جواب بهینه است.

الگوریتم روش شاخه و کرانه

در ادامه خلاصه روش حل مسائل برنامه ریزی عدد صحیح به روش شاخه و کرانه به صورت الگوریتمی ‌بیان می‌شود:

مثال: مسئله تخصیص کار به نفر زیر را در نظر بگیرید. هدف این است که هر کدام از کارها منحصرا به یکی از چهار نفر طوری تخصیص داده شود که مجموع هزینه‌های انجام شده حداقل شود.

 

حل:

تکرار صفر:

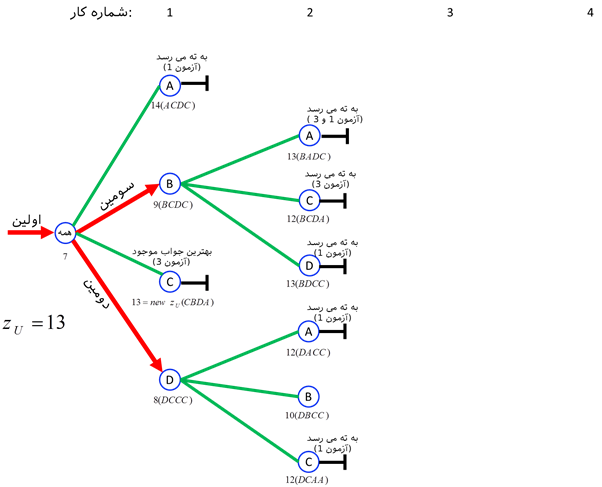
این مسئله دارای !4=24 ترکیب مختلف از جواب‌ها است. حد پایین این 24 جواب را با z_L نشان می‌دهیم. برای چنین حد پایینی، جمع کردن حداقل‌ های ممکن هزینه‌های تخصیص ( یعنی مجموع اعداد حداقل ستون‌های جدول هزینه) در نظر گرفته می‌شود که در این مثال برابر با 2+1+2+2=7 می‌شود. این جواب مربوط به تخصیص DCDC است که واضحا یک جواب غیرموجه است.

تکرار 1:

با تخصیص کار 1 به هر کدام از افراد آغاز می‌کنیم و کل جواب‌ها را به 4 زیر مجموعه تخصیص می‌دهیم. برای مثال، حد پایین z_L برای تخصیص کار 1 به نفر A برابر با 14=9+(1+2+2) می‌شود. به این صورت که 9 هزینه تخصیص کار 1 به نفر A است و حداقل هزینه‌ها برای مابقی کارها به شرط این که به فرد A دیگر کاری تخصیص داده نشود. حد پایین برای کار 1 به نفر B، برابر با 9=4+(1+2+2) می‌شود. برای تخصیص کار 1 به فرد C، حد پایین برابر 13=3+(3+2+5) می‌شود. برای تخصیص کار 1 به فرد D، حد پایین z_L برابر با 8=2+(1+3+2) می‌شود.

چون z_L برای زیر مجموعه C، منجر به جواب موجه CBDA می‌شود، لذا حد بالایی جواب بهینه نیز به صورت z_U=13 به هنگام می‌شود و CBDA جواب بهینه فعلی می‌شود. طبق آزمون 3، زیر مجموعه C به ته می‌رسد. با توجه به آزمون 1، زیر مجموعه A به ته می‌رسد و لذا تنها دو مجموعه B و D برای انشعاب باقی می‌ماند. خلاصه نتایج در شکل زیر آمده است.

تکرار 2:

از بین دو زیر مجموعه باقی مانده، زیر مجموعه D به دلیل این که کمترین حد پایین را دارد انتخاب می‌شود. به این اصل، اصل بهترین حد گفته می‌شود. در این زیر مجموعه که کار 1 به فرد D تخصیص داده می‌شود و در این زیر مجموعه، می‌توان 3 زیر مجموعه DA، DB، و DC منشعب کرد که حد پایین به ترتیب برابر با 12، 10، و 12 می‌شود. برای این سه زیر مجموعه، هیچ یک از آزمون‌های توقف برقرار نیست. لذا زیر مجموعه‌های باقی مانده عبارتند از B، DA،DB و DC. نتایج این تکرار در شکل زیر آمده است.

تکرار 3:

از بین چهار زیر مجموعه باقی مانده، زیر مجموعه B به دلیل کمترین حد پایین انتخاب می‌شود و انتخاب به سه زیر مجموعه BA،BC، BD منشعب می‌شود. حد پایین آن‌ها به ترتیب برابر با 4+5+(2+2)=13 ، 4+1+(2+5)=12 و 13=4+4+( 3+2) خواهد بود. چون زیر مجموعه‌های BA و BC جواب‌های موجه هستند و حد پایین زیر مجموعه‌های BA و BD برابر حد بالای هستند، لذا هر سه زیر مجموعه به ته می‌رسند.

همچنین چون زیر مجموعه BC یک جواب موجه است مقدار تابع هدف در آن از z_U فعلی کمتر است، لذا جواب BCDA بهترین جواب موجه جدید محسوب می‌شود. از آن جاییکه z_U=12 برابر با z_L زیر مجموعه‌های DA و DC است، لذا این دو مجموعه نیز به ته می‌رسد. بنابراین، تنها زیر مجموعه‌ای که تا این لحظه به جا مانده است، DB است. نتایج این تکرار در شکل زیر آمده است

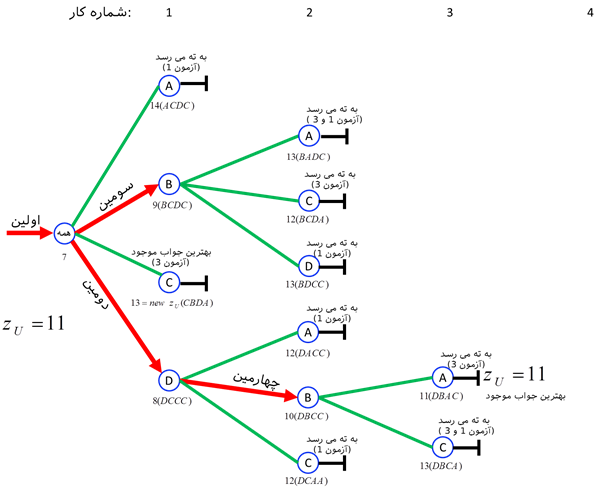
تکرار 4:

تنها زیر مجموعه باقی مانده، DB است که به زیر مجموعه‌های DBA و DBC تقسیم می‌شود. حد پایین آن‌ها به ترتیب 2+3+4+(2)=11 و 2+3+3+(5)=13 است. چون این دو حد مربوط به جواب‌های موجه می‌شوند، لذا هر دو زیر مجموعه به ته می‌رسند. علاوه بر این‌ها، جواب موجه DBAC مربوط به زیر مجموعه DBA از بهترین جواب موجود بهتر است ( 11<12 )، لذا این جواب (DBAC) به عنوان جواب جدید انتخاب می‌شود. چون زیر مجموعه‌ای دیگر که هنوز به ته نرسیده باشد، باقی نمانده است، لذا بهترین جواب موجه (یعنی DBAC)، جواب بهینه است و الگوریتم به پایان می‌رسد. خلاصه محاسبات این تکرار در شکل زیر آمده است.

در مثال فوق، از قاعده بهترین حد برای انتخاب شاخه‌ها استفاده شد. قاعده دیگر در انتخاب شاخه روش جدیدترین حد است که از جدیدترین حد بدست آمده برای شاخه کردن استفاده می‌شود.

الگوریتم شاخه و کرانه برای برنامه‌ریزی صفر و یک

همان طور که در بخش قبلی گفته شده، بسیاری از مسائل برنامه ریزی عدد صحیح به صورت متغیرهای صفر و یک هستند. اما در برخی از مسائل، متغیرها می‌توانند بیش از دو مقدار به خود بگیرند. ولی می‌توان این مدل‌ها را به متغیرهای دودویی تبدیل کرد. فرض کنید که x یک عدد صحیح باشد. در این صورت می‌توان گفت

که

در این حالت، y_i متغیرهای کمکی از نوع صفر و یک هستند.

برای ارایه دستور حل شاخه و کرانه برای مسئله برنامه ریزی عدد صحیح دودویی، مسئله‌ای عمومی ‌به صورت زیر را در نظر بگیرید.

که در مدل فوق داریم.

این فرض در واقع محدودیتی ایجاد نمی‌کند. زیرا اگر c_j<0 باشد، می‌توان xj را با (1-x’_j)- جایگزین کرد که در این صورت ضریب متغیر x’_j در تابع هدف مثبت خواهد شد. با توجه به موارد فوق، الگوریتم شاخه و کرانه به صورت زیر ارایه می‌گردد.

برای روشن شدن موضوع مثال زیر را حل می‌کنیم.

تمرین: مسئله برنامه ریزی عدد صحیح زیر را حل نمایید.

حل:

تکرار صفر:

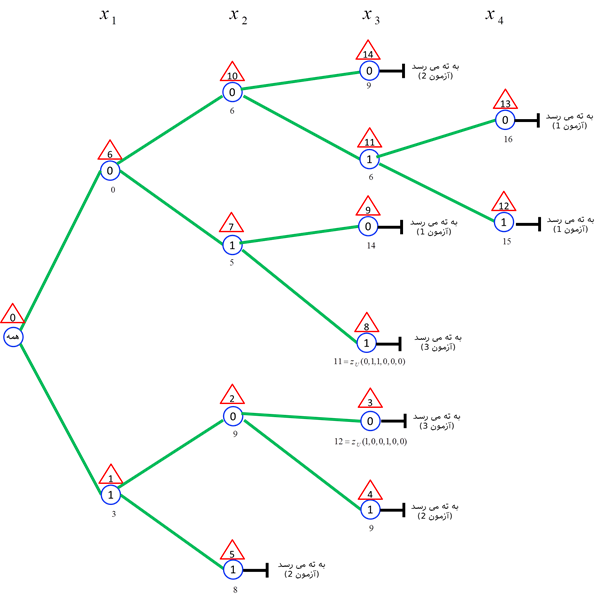
z_U=∞ و چون ضریب متغیرها در تابع هدف نامنفی هستند، لذا مقدار بهینه تابع هدف قطعا از صفر بزرگتر است و لذا z_L=0. چون جواب (0,0,0,0,0,0) در محدودیت‌های 1 و 3 امکان پذیر نیست، لذا شرایط توقف برقرار نیست و باید این گره، شاخه کرد و این گره به دو شاخه x₁=1 و x₁=0 تقسیم می‌شود.

تکرار 1: جواب جزیی (1) بررسی می‌شود:

آزمون 1:

آزمون 2:

این گره در این آزمون به ته نمی‌رسد.

آزمون 3: جواب (1,0,0,0,0,0) بررسی می‌شود که محدودیت‌ها برقرار یا نه؟

این گره در آزمون 3 بسته نمی‌شود.

تکرار 2: گره با جواب جزیی (1,0) بررسی شود:

آزمون 1:

آزمون 2:

آزمون 3: جواب (1,0,1,0,0,0) را از نظر برقراری در محدودیت‌ها بررسی شود.

این گره در آزمون 3 بسته نمی‌شود.

تکرار 3: جواب جزیی (1,0,0) بررسی شود.

آزمون 1:

آزمون 2:

آزمون 3: با توجه به این که جواب جزیی (1,0,0) است، باید جواب (1,0,0,1,0,0) کنترل شود که در محدودیت‌ها برقرار است یا نه؟

جواب (1,0,0,1,0,0) امکان‌پذیر است و لذا z_U=12.

تکرار 4: جواب جزیی (1,0,1) در نظر بگیرید

آزمون 1:

آزمون 2:

چون محدودیت 1 برقرار نیست لذا این گره با توجه به آزمون 2 به ته می‌رسد.

تکرار 5: جواب جزیی (1,1) را در نظر بگیرید.

آزمون 1:

 

آزمون 2:

این گره به ته می‌رسد.

تکرار 6: جواب جزیی (0) را در نظر بگیرید.

آزمون1:

آزمون 2:

با این آزمون به ته نمی‌رسد.

آزمون 3: چون x₁=0 است، باید کنترل شود که (0,1,0,0,0,0) امکان پذیر است یا نه؟

در این آزمون، گره به ته نمی‌رسد.

تکرار 7: جواب جزیی (0,1) را در نظر بگیرید.

آزمون 1:

آزمون 2:

آزمون 3: جواب (0,1,0,0,0,0) بررسی شود.

تکرار 8: جواب جزیی (0,1,1) را در نظر بگیرید.

آزمون 1:

آزمون 2:

آزمون 3: جواب (0,1,1,0,0,0) کنترل شود.

این گره با آزمون 3 به ته می‌رسد و z_U=11 بهترین جواب موجه فعلی است.

تکرار 9: جواب جزیی (0,1,0) را در نظر بگیرید.

آزمون 1: چون رابطه زیر برقرار است و لذا این گره بسته می‌شود.

تکرار 10: جواب جزیی (0,0) را در نظر بگیرید.

آزمون 1:

آزمون 2:

آزمون 3: جواب (0,0,1,0,0,0) را بررسی کنید.

این گره به ته نمی‌رسد.

تکرار 11: جواب جزیی (0,0,1) را در نظر بگیرید.

آزمون 1:

آزمون 2:

آزمون 3: جواب (0,0,1,0,0,0) کنترل شود.

تکرار 12: جواب جزیی (0,0,1,1) را در نظر بگیرید.

آزمون 1: چون رابطه زیر برقرار است

و لذا این گره بسته می‌شود.

تکرار 13: جواب (0,0,1,0) را در نظر بگیرید.

آزمون 1: چون رابطه زیر برقرار است

لذا این گره بسته می‌شود.

تکرار 14: جواب (0,0,0) را در نظر بگیرید.

آزمون 1:

آزمون 2:

این گره با آزمون 2 به ته می‌رسد.

کلیه گره‌ها بسته شده است و جواب بهینه z=11 و (0,1,1,0,0,0) می‌شود. خلاصه محاسبات در شکل زیر آمده است.

الگوریتم شاخه و کرانه برای برنامه‌ریزی مختلط

مدل برنامه‌ریزی عدد صحیح زیر را در نظر بگیرید:

در مدل فوق، اگر I=n باشد مدل برنامه‌ریزی عدد صحیح خالص (Pure integer programming) خواهیم داشت. برای حل مدل فوق الگوریتم زیر ارایه می‌شود.

با حذف محدودیت عدد صحیح و حل مسئله برنامه‌ریزی خطی آزاد شده انجام می‌شود. اگر جواب حاصل به ازإی تمامی متغیرهای عدد صحیح، مقدار صحیح به خود بگیرد، در این صورت جواب بهینه بدست آمده است. در غیر این صورت، در هر تکرار متغیری مانند x_j را بر می‌گزیند که مقدار آن عدد صحیح نباشد به طوری که اگر k عدد صحیح باشد،

سپس زیر مجموعه موجود را دو زیر مجموعه جدید تقسیم می‌کند.

• جواب‌هایی که در آن x_j≤k
• جواب‌هایی که در آن x_j≥1+k

با حذف شرط صحیح بودن و حل مسئله برنامه‌ریزی خطی آزاد شده (با اضافه کردن محدودیت‌های x_j≤k یا x_j≥1+k ) یک حد بالا ( z_U ) برای زیر مجموعه بدست می‌آید. جواب مسئله آزاد شده توسط روش سیمپلکس ثانویه بدست می‌آید. آزمون‌های به ته رسیدگی به صورت سه آزمون زیر است:

آزمون 1: z_L≥z_U

آزمون 2: با روش سیمپلکس ثانویه در می‌یابیم که جواب موجهی وجود ندارد.

آزمون 3: در جواب بهینه، تمام متغیرهای (x_j (j=1,…,I عدد صحیح باشند.

اگر زیر مجموعه‌ای با آزمون 3 به ته رسید و z_L < z_U باشد، آنگاه z_L = z_U قرار داده شده و این جواب را به عنوان بهترین جواب موجود ذخیره می‌شود. پس از آن که تمامی ‌زیر مجموعه‌های باقی مانده به ته رسیدند، آنگاه حد پایین همان جواب بهینه است.

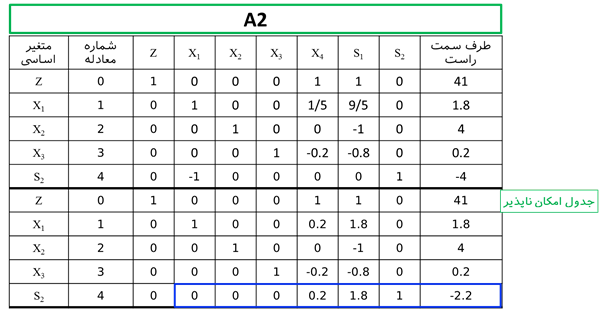
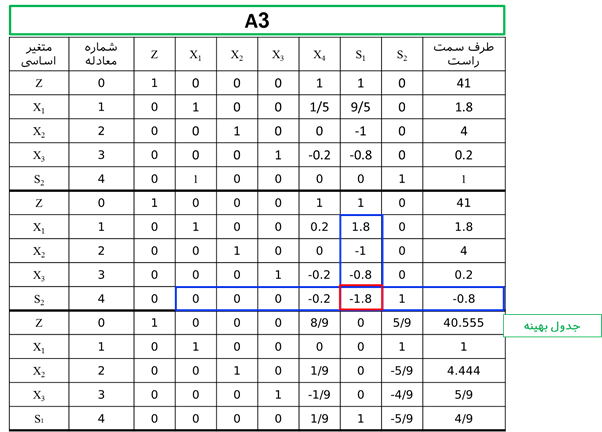
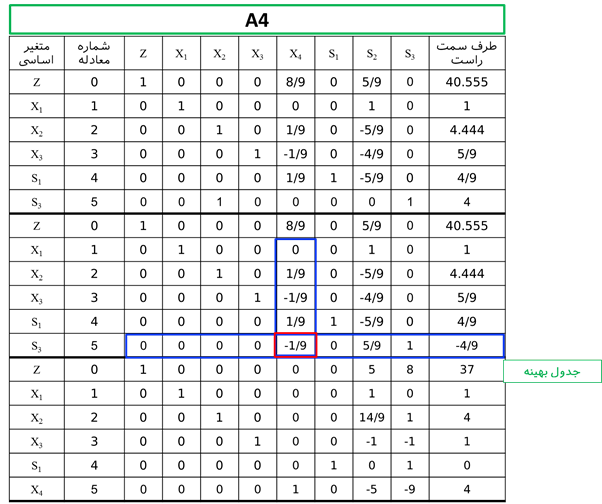
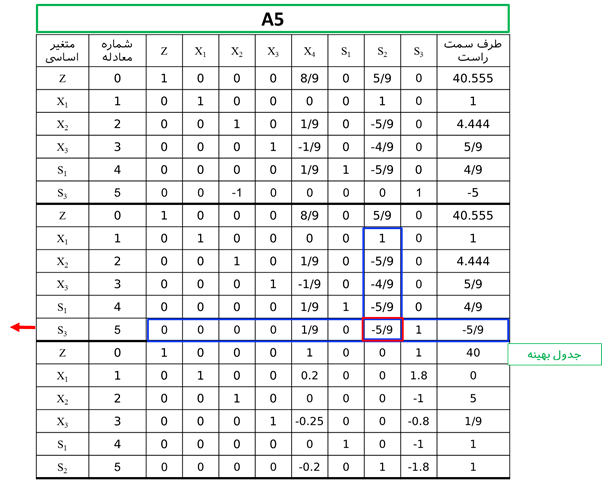
مثال: مدل برنامه‌ریزی عدد صحیح زیر را از روش شاخه و کرانه حل نمایید.

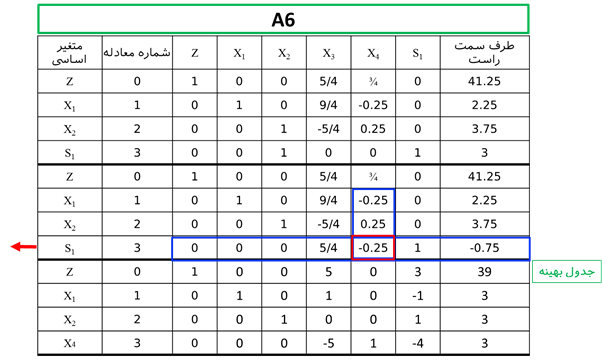
حل: فرم استاندارد مدل فوق به صورت زیر است:

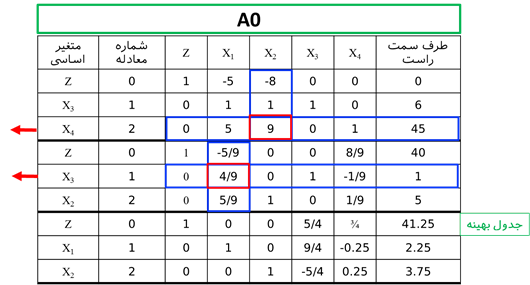
متغیر x₁ و x₂ دارای مقدار غیر صحیح در جواب بهینه است. لذا یکی از متغیرها را باید برای شاخه کردن انتخاب کرد که در این مرحله x₂ انتخاب می‌شود.

 

 

با توجه به این که ضرایب متغیرها در معادله شماره 4 مثبت است و سمت راست منفی است، لذا این جواب امکان ناپذیر است.

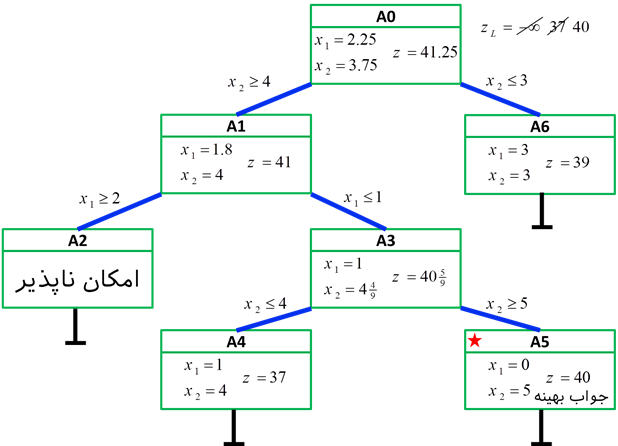
کلیه مراحل حل را می‌توان در درخت زیر نشان داد.

حل مسائل برنامه ریزی عدد صحیح به روش شاخه و کرانه

حل مسائل برنامه ریزی عدد صحیح به روش شاخه و کرانه

حل مسائل برنامه ریزی عدد صحیح به روش شاخه و کرانه