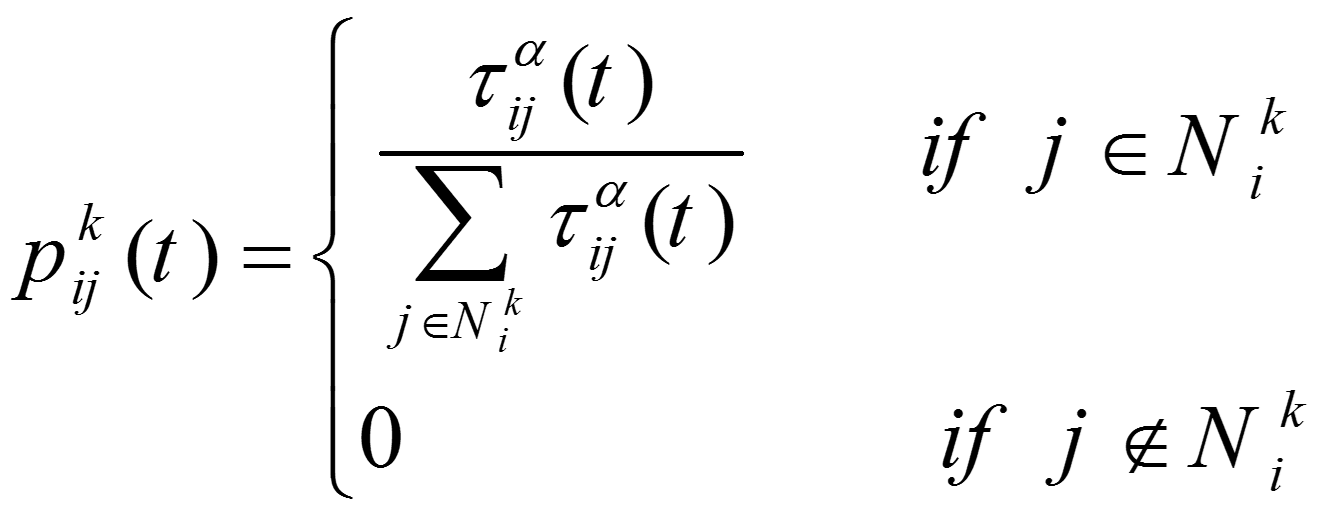الگوریتم اجتماع مورچگان

درس 18: الگوریتم اجتماع مورچگان یا الگوریتم کلونی مورچگان

تهیه شده توسط گروه بهینه یاب

مقدمه

محاسبه راه حل بهینه یا Optimal solution برای اکثر مسایل بهینه سازی که در خیلی از زمینه‌های کاربردی و عملی مشاهده می‌گردند، کار دشوار و سختی است. در عمل، معمولا به راه حل‌های خوب که از الگوریتم‌های هیوریستیک Heuristic یا متاهیوریستیک (همان فراابتکاری) Metaheuristic بدست می‌آید، اکتفا می‌گردد. متاهیوریستیک‌ها مجموعه ای از فنون بهینه سازی تقریبی Approximate optimization techniques را که عمدتا در طول دو دهه گذشته شهرت پیدا کرده اند، در بر می‌گیرند. روش‌های فراابتکاری راه حل‌های قابل قبول در زمان معقول را برای مسایل پیچیده و سخت، در زمینه‌های مهندسی و علوم پایه ارایه می نمایند. برخلاف الگوریتم‌های بهینه سازی دقیق Exact optimization algorithms ، فراابتکاری‌ ها بهینه بودن جواب‌های بدست آمده را ضمانت نمی نمایند.

کلمه متاهیوریستیک از کلمه یونانی “Heuriskein” به معنای هنر کشف قواعد جدید برای حل مسایل گرفته شده است. پیشوند “متا” نیز از یک کلمه یونانی به معنای “متدولوژی” سطح بالا گرفته شده است. واژه ” متاهیوریستیک ” اولین بار توسط گلوور در سال 1986 ارایه گردید. روش جستجوی متاهیوریستیک را می توان به صورت متدولوژی‌های عمومی سطح بالایی که می توانند به عنوان یک استراتژی راهنما در طراحی هیورستیک‌های اختصاصی برای حل مسایل بهینه سازی تخصصی به کار روند، تعریف کرد. الگوریتم اجتماع مورچگان

برخلاف روش‌های دقیق، متاهیوریستیک‌ها (فراابتکاری‌‌ها) برای مسایل با اندازه‌های بزرگ کاربرد دشوار دارد و راه حل‌هایی راضی کننده ای در زمان معقولی ارایه می نمایند. در این الگوریتم‌ها، هیچ گونه ضمانتی برای یافتن جواب بهینه سراسری یا حدودی از آن وجود ندارد. متاهیوریستیک‌ها (فراابتکاری‌‌ها) در طول بیست سال گذشته شهرت زیادی پیدا کرده اند. کاربرد و استفاده از آن‌ها در خیلی از مسایل، کارایی و اثر بخشی آن‌ها را برای حل مسایل پیچیده و بزرگ نشان می دهد. فراابتکاری‌ها در خیلی از زمینه‌ها از قبیل موارد زیر کاربرد دارند:

• طراحی مهندسی، بهینه سازی توپولوژی، بهینه سازی مسایل الکترونیک، آئرودینامیک، دینامک سیالات، مخابرات، رباتیک
• یادگیری ماشین و کاوش داده‌ها
• مدل سازی سیستم‌ها، شبیه سازی و تحقیق در شیمی، فیزیک، بیولوژی، کنترل، سیگنال، و پردازش تصویر
• مسایل مسیردهی و برنامه ریزی، برنامه ریزی ربات، مسایل تولید و زمان بندی، حمل و نقل و لجستیک، مدیریت زنجیره تامین

روش‌های مختلف الگوریتم‌های فراابتکاری یا متاهیوریستیک تا به حال پیشنهاد شده است که به صورت زیر است:

• بهینه سازی کلونی مورچگان Ant colony optimization
• بهینه سازی کلونی زنبوران Bee colony
• الگوریتم‌های ترتیبی cultural algorithms
• الگوریتم‌های با هم تکاملی Co-evolutionary algorithms
• الگوریتم ژنتیک Genetic algorithm
• جستجوی محلی تکراری Iterated local search
• بهینه سازی توده ذرات particle swarm intelligent
• انجماد تدریجی Simulated Annealing
• جستجوی ممنوع Taboo search
• جستجوی همسایگی متغیر Variable neighboar search

در طراحی یک فراابتکاری‌، دو معیار متناقض شامل کاوش (Exploration) و در فضای جستجو (گوناگونی و تنوع) و تبعیت (Exploitation) از بهترین راه حل‌های پیدا شده، باید در نظر گرفته شوند. در کاوش در ناحیه‌های جستجو نشده بررسی صورت می‌گیرد. در تبعیت، در ناحیه‌های امید بخش که تا به حال در آن ناحیه یک جواب خوب پیدا شده است بررسی بیشتر صورت می‌گیرد. در صورتیکه به کاوش اهمیت بیشتری داده شود، الگوریتم رفتار تصادفی بیشتری خواهد داشت و به سمت رفتار تصادفی میل می کند و در صورتی که به رفتار تبعیت توجه بیشتری شود، الگوریتم از رفتار تصادفی فاصله می‌گیرد و جستجو تنها در محدوده راه حل‌های خوب به جستجو می پردازد.الگوریتم اجتماع مورچگان

معیار‌های طبقه بندی زیادی ممکن است برای طبقه بندی فراابتکاری‌‌ها استفاده شود که در زیر به بعضی از آن‌ها اشاره می‌شود:

الهام گرفته از طبیعت در مقابل عدم الهام از طبیعت

خیلی از الگوریتم‌های فراابتکاری از فراینده‌های طبیعی الهام گرفته شده اند: از قبیل الگوریتم‌های اجتماع مورچگان و زنبور عسل که از هوش توده ای از گونه‌های مختلف مورچگان و زنبوران استفاده می کنند.

نحوه استفاده از حافظه

بعضی از الگوریتم‌های فراابتکاری از قبیل انجماد تدریجی بدون حافظه هستند و حرکت‌های قبلی را در جایی ذخیره نمی کنند. در مقابل الگوریتم انجماد تدریجی از یک حافظه که بعضی از اطلاعات را در طول جستجو بدست می‌آورد، ذخیره می کند.

قطعی در مقابل احتمالی

یک الگوریتم قطعی، یک مسئله بهینه سازی را از طریق تصمیم گیری قطعی حل می نماید(برای مثال الگوریتم جستجوی محلی و جستجوی ممنوع). در الگوریتم‌های فراابتکاری احتمالی، بعضی از قواعد احتمالی در فرایند جستجو مورد استفاده قرار می‌گیرد که می توان به الگوریتم انجماد تدریجی و الگوریتم ژنتیک اشاره کرد. در الگوریتم‌های قطعی، با داشتن یک راه حل اولیه و اجراهای متفاوت، تنها یک جواب نهایی بدست می‌آید و در حالی که در الگوریتم‌های تصادفی، با داشتن یک راه حل اولیه و اجرا‌های متفاوت، ممکن است که جواب‌های نهایی متفاوتی بدست آید.

تکراری در مقابل حریصانه

در الگوریتم‌های تکراری، الگوریتم با یک راه حل کامل شروع شده و در هر تکرار راه حل یا راه حل‌ها تغییر پیدا می کنند. در الگوریتم‌های حریصانه یک راه حل کامل در اختیار نبوده بلکه با یک راه حل ساخته نشده شروع شده و در هر مرحله، یک متغیر تصمیم از مسئله یک قسمت از راه حل را می سازد. اغلب الگوریتم‌های فراابتکاری، الگوریتم‌های تکراری هستند.

در ادامه الگوریتم اجتماع مورچه که الگوریتمی است که از طبیعت الهام گرفته است و در رده الگوریتم‌های احتمالی، و حریصانه با حافظه قرار می‌گیرد صحبت می‌شود.

معرفی الگوریتم اجتماع مورچگان یا الگوریتم کلونی مورچگان

مورچه ها بر روی زمین از حدود 100 میلیون سال پیش زندگی می‌کرده اند و در حال حاضر جمعیتی در حدود 10¹⁶ در دنیا دارند. تخمین زده شد که مجموع وزن مورچه ها در حدود مجموع وزن انسان‌های روی زمین می‌باشند. این حشرات موجوداتی اجتماعی می‌باشند و در کلونی هایی به اندازه ای از 30 تا میلیون ها فرد زندگی می‌کنند. رفتارهای پیچیده کلونی مورچگان، انسان ها را تشویق کرده است که مطالعات متعددی در خصوص رفتارهای اجتماعی و فردی آن ها داشته باشند. رفتارهای گروهی از مورچگان در ارتباط با جستجو برای غذا، نظم کارگران، سازماندهی گورستان، مواظبت از بچه ها و ساختن لانه مورد مطالعه قرار گرفته است.

رفتارهای پیچیده مورچه ها، از رفتارهای جمعی مورچه‌های تکی خیلی ساده و بی حیله ناشی می‌شود. یک مورچه براساس اطلاعاتی که از محیط اطراف خود به دست می‌آورد، اقدام ساده ای را انجام می‌دهد که پایه ای تصادفی دارد.

یکی از اولین رفتارهایی که توسط محققین مورد مطالعه قرار گرفت، توانایی مورچه ها در یافتن کوتاهترین مسیر بین یک منبع غذا و لانه آن ها بود. بر اساس این مطالعات، اولین الگوریتم از رفتار مورچه ها در جستجوی غذا توسط مارکو دوریگو Marco Dorigo ارایه گردید که خروجی رساله دکترای ایشان در دانشگاه میلان ایتالیا بود.

رفتار مورچه ها در جستجوی غذا

چگونه مورچه ها می‌توانند کوتاهترین مسیر بین محل غذا و لانه خود را بدون هیچ گونه مکانیسم هدایتی دیداری و مرکزی پیدا کنند؟ مطالعات رفتارهای بعضی از گونه‌های واقعی مورچه ها نشان داده است که یک الگوی تصادفی و شانسی در حرکت مورچه ها برای یافتن غذا وجود دارد. به محض این که یک منبع غذا در محلی در حوالی لانه مورچه ها قرار داده می‌شود، رفتار تصادفی به مروز سازماندهی بیشتری یافته و در نهایت منجر به رسیدن به یک مسیر مشابه توسط مورچه ها به این محل خواهد شد و به صورت جادویی دیده می‌شود که مورچه ها کوتاهترین مسیر را پیدا کرده اند. این رفتار عجیب نتیجه تاثیر مورچه هایی است که منبع غذا را پیدا کرده اند. مورچه هایی که غذا را یافته اند با سایر مورچه ها از طریق یک مکانیسم ارتباطی به نام اثر فرومون Pheromone Trails ارتباط برقرار می‌نمایند. زمانی که یک مورچه یک منبع غذا را پیدا می‌کند و مقدار غذا به خانه می‌برد، در مسیر حرکت خود ماده شیمیایی به نام فرومون منتشر می‌نماید. بقیه مورچه ها که به دنبال غذا می‌گردند، در هنگام انتخاب مسیر به غلظت فرومون مسیر توجه می‌نمایند. مسیرهای با غلظت فرومون بیشتر، احتمال بیشتری برای انتخاب دارند. هر چقدر مورچه‌های بیشتری از یک مسیر عبور نمایند، غلظت فرومون آن مسیر افزایش یافته و در نتیجه، مورچه‌های بیشتری نیز نسبت به آن مسیر علاقه مند می‌شوند.

ساختار عمومی بهینه سازی اجتماع مورچگان یا (الگوریتم کلونی مورچگان)

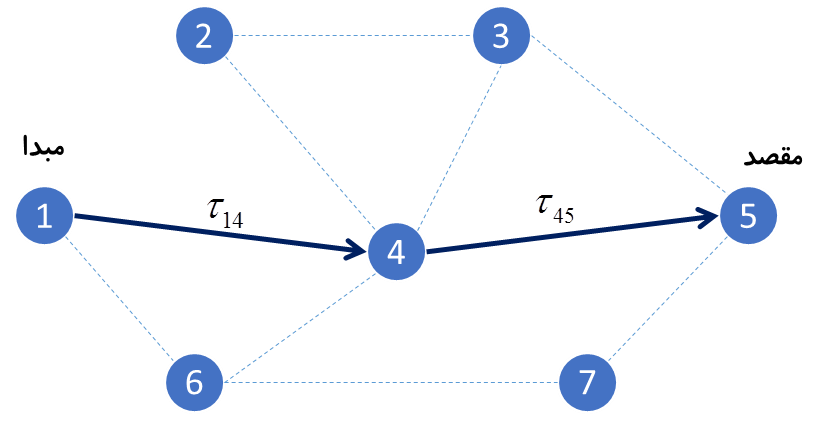
مساله یافتن کوتاهترین مسیر بین دو راس در یک گراف (G=(V,E است که V مجموعه راس‌های و E ماتریسی است که ارتباطات بین راس ها را بیان می‌کند. این گراف |V| راس دارد. طول، L^k، که توسط مورچه k ام ساخته شده است، به صورت فاصله مبدا تا مقصد تعریف می‌گردد. یک گراف نمونه همراه با یک مسیر انتخابی، در شکل زیر نمایش داده شده است. طول مسیر انتخابی برابر با 2 است. در این حالت، یک غلظت فرومون T_ij به هر یال (i,j) از گراف، تخصیص داده می‌شود.

در الگوریتم استاندارد بهینه سازی اجتماع مورچگان یا همان SACO که مخفف Simple Ant Colony Optimization است، در ابتدا به هر یال، یک مقدار تصادفی به عنوان فرومون اولیه، T_ij⁰، تخصیص داده می‌شود. در ابتدای الگوریتم به علت نبود غلظت فرومون یا مقدار خیلی کم آن، مورچه ها به طور تصادفی مسیرها را انتخاب می‌نمایند. تعدادی از مورچه ها، k=1,…,n ، در راس مبدا قرار داده می‌شود. در هر تکرار از الگوریتم SACO، هر مورچه به صورت مرحله به مرحله یک مسیر یا راه حل را بین مبدا و مقصد می‌سازد. در هر راس، هر مورچه فرایند تصمیم گیری را برای تعیین یال بعدی مسیر خود به کار می‌برد. اگر مورچه k در راس i قرار داشته باشد، راس بعدی که در همسایگی راس i قرار دارد را بر اساس یک تابع احتمال گذر به شکل زیر تعیین می‌نماید.

که در آن N_i^k مجموعه یال‌های قابل انتخاب برای مورچه k ام در راس i است. در واقع N_i^k مجموعه یال‌های همسایه ای راس i است. در صورتیکه مجموعه N_i^k تهی باشد آنگاه راس پیشین راس i در نظر گرفته می‌شود و در واقع در صورتیکه مورچه به مسیر بسته برسد، برمی گردد. این مساله منجر به ایجاد یک حلقه می‌گردد، ولی مشکلی را ایجاد نمی کند زیرا پس از رسیدن به مقصد، در هنگام معرفی مسیر بین مبدا و مقصد، حلقه ها توسط مکانیزمی حذف می‌گردند. در معادله بالا، a یک مقدار ثابت مثبت برای شدت بخشیدن به اثر غلظت فرومون است. مقدار بزرگ a، اهمیت غلظت فرومون را افزایش داده و تاثیر رفتارهای تصادفی را کمتر می‌کند و منجر به همگرایی سریع به سمت یک بهینه محلی می‌گردد.

بعد از آن که تمامی مورچه ها، یک مسیر کامل بین مبدا تا مقصد را ساختند و حلقه‌های احتمالی حذف شدند، هر مورچه ردپای خود را به سمت راس مبدا دنبال می‌نماید و مقداری فرومون در هر یال (i,j) روی مسیر طی شده، مطابق با قاعده زیر با نام * منتشر می‌نماید.

(L_k(t معرف طول مسیر ساخته شده توسط مورچه k-ام در مرحله زمانی t می‌باشد. در نتیجه، میزان غلظت فرومون هر مسیر مطابق با قاعده زیر به هنگام می‌گردد

که در رابطه فوق، n_k تعداد مورچه ها می‌باشد. با استفاده از رابطه ارایه شده در * مقداری فرومون روی هر یال تولید می‌گردد و این مقدار بستگی به کیفیت مسیرهایی دارد که توسط مورچه ها با استفاده از آن یال ساخته شده است. به عبارت دیگر، هر مورچه مقداری فرومون در هر یال متناسب با کیفیت مسیرش به جا می‌گذارد. بعد از یک تکرار، میزان فرومون موجود در یک یال با توجه به مورچه‌های عبوری از آن یال تغییر می‌یابد. مقدار چگالی اضافه شده با مقدار قبلی چگالی فرومون آن مسیر طبق معادله فوق به هنگام می‌شود.

الگوریتم سیستم مورچه یا AS یکی از الگوریتم های معروف الگوریتم اجتماع مورچگان است. برای مطالعه