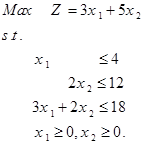.

درس 1: برنامه ریزی خطی

تهیه شده توسط گروه آموزشی بهینه یاب

تحقیق در عملیات چیست؟

تحقیق در عملیات را برخوردی علمی با تصمیم گیری هایی دانست که در جریان عملیات سیستم‌های سازمان یافته انجام می‌گیرند. به عبارت دیگر تحقیق در عملیات در رابطه با مسائل مربوط به هدایت و هماهنگی عملیات و فعالیت‌های گوناگون به کار گرفته می‌شود. تحقیق در عملیات در زمینه‌های گوناگونی نظیر اقتصاد، تجارت، صنعت، دولت ، بهداشت و غیره مورد استفاده قرار می‌گیرد. تحقیق در عملیات به مسائل با نگرشی نظام گرا (systematic) بررسی می نماید و کوشش می‌کند تا تضاد منابع بخش‌های مختلف یک سازمان را به طوری حل نماید که بهترین نتیجه یا همان جواب بهینه برای کل سازمان ایجاد شود.

تحقیق در عملیات شامل بخش‌های مختلفی است که برنامه ریزی خطی ریاضی یکی از مهمترین بخش‌های آن است. در برنامه ریزی خطی از مدلی ریاضی به منظور تشریح مسئله مورد نظر استفاده می‌شود. کلمه خطی به معنای آن است که تمام روابط ریاضی این مدل لزوما باید خطی باشند. تولد برنامه ریزی خطی به سال 1947 میلادی باز می‌گردد که در آن زمان جورج دانتزیگ (George Dantzig) برای پروژه محاسبات علمی برنامه‌های بهینه، روش سیمپلکس را برای حل مسائل عمومی برنامه ریزی خطی ابداع کرد. به قدری این ابداع در علم مدیریت تاثیر گذار بود که جورج دانتزیگ را تا پای جایزه نوبل پیش برد ولی هیچگاه موفق به گرفتن این جایزه نشد.

فرموله کردن مسئله به صورت برنامه‌ریزی خطی

این بخش را با فرمول بندی یک مثال کوچک برنامه ریزی خطی ادامه می‌دهیم. این مثال به اندازه کافی ساده است که می‌توان آن را به صورت گرافیکی مورد بررسی قرار داد.

مثال: یک شرکت تولیدی درب و پنجره، دارای سه کارگاه است. در کارگاه 1 قاب‌های آلومینیومی و قسمت‌های فلزی تولید می‌شود. در کارگاه 2، قاب‌های چوبی تولید می شود و در کارگاه 3، برش شیشه و سوار کردن آن به قاب ها انجام می‌شود. مدیریت این کارگاه ها به دنبال تولید دو محصول جدید هستند و از مرکز تحقیق در عملیات خواسته اند که میزان تولید از هر محصول را با توجه به ظرفیت کارگاه چند واحد است. محصول 1، دری با قابی آلومینیومی و محصول 2 پنجره‌ای شیشه با قاب چوبی است. با توجه به این که هر دو محصول برای جوشکاری نیاز به کارگاه 3 دارد، ظرفیت این گارگاه باعث می‌شود که رقابتی بین این دو محصول ایجاد شود. در جدول زیر سود هر محصول، میزان استفاده از منابع و ظرفیت هر کارگاه آورده شده است.

x₁ و x₂ به ترتیب تعداد محصولات 1 و 2 در هر دقیقه است و z نشان دهنده سود حاصل از فروش در هر دقیقه است. در ادبیات تحقیق در عملیات به x₁ و x₂ متغیرهای تصمیم‌گیری (decision variables) و z را تابع هدف (objective function) گفته می‌شود.

برای تولید هر واحد محصول 1، 1 واحد از کارگاه 1 مصرف می‌شود که در هر دقیقه کارگاه 1 تنها 4 واحد ظرفیت برای محصول جدید موجود دارد. این محدودیت به صورت جبری x₁ ≤ 4 نمایش داده می‌شود. به طور مشابه برای کارگاه شماره 2، محدودیت 2x₂ ≤ 12 برای محصول 2 مورد نیاز است. ظرفیت کارگاه 3 توسط هر دو محصول استفاده می‌شود که باعث محدودیت 3x₁ + 2x₂ ≤ 18 می‌شود. چون محصول ها نمی‌توانند منفی باشند، متغیرهای تصمیم‌گیری نامنفی هستند و نمایش ریاضی آن به صورت x₁ ≥ 0 و x₂ ≥ 0 می‌شود. به طور خلاصه نمایش ریاضی مدل برنامه ریزی خطی این مسئله به صورت زیر می‌شود.

به دلیل این که این مدل برنامه‌ریزی خطی شامل تنها دو متغیر x₁ و x₂ است، می‌توان برای حل آن از روش ترسیمی بهره برد. این شیوه مستلزم رسم یک شکل با محورهای x₁ و x₂ است. هر یک از محدودیت‌ها بخشی از محور دوبعدی را پوشش می‌دهد که از اشتراک این محدودیت‌ها، فضای موجه یا امکان پذیر مسئله ایجاد می‌شود. ما به دنبال نقطه‌ای هستیم که بیشترین مقدار عبارت z را ایجاد می‌کند. برای رسم ناحیه امکان پذیر محدودیت‌ها را تک تک به صورت زیر اضافه می‌کنیم.

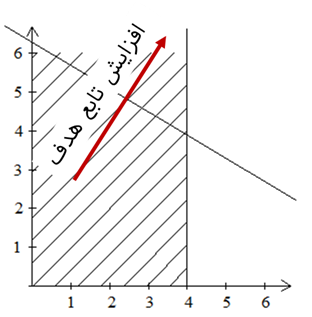
توجه: برای اضافه کردن محدودیت 3x₁ + 2x₂ ≤ 18 به فضای امکان پذیر، کافی است که خط 3x₁ + 2x₂ = 18 را ابتدا رسم کنید. با توجه به این که نقطه مبدا ( x₁ =0 و x₂ = 0 ) در رابطه 3∗0+2∗0 ≤ 18 صدق می‌کند، فضای زیر خط 3x₁ + 2x₂ = 18 بیان ترسیمی محدودیت است. تنها گام باقی مانده یافتن نقطه‌ای است که مقدار 3x₁ + 5x₂ = z را در منطقه امکان پذیر بیشینه شود. فرض کنید که z = 10 باشد. اگر این مقدار در محدوده امکان پذیر قرار گرفت می‌توان این مقدار را افزایش داد. در غیر این صورت z را به نحوی باید تغییر داد تا در محدودیت امکان پذیر جا بگیرید.

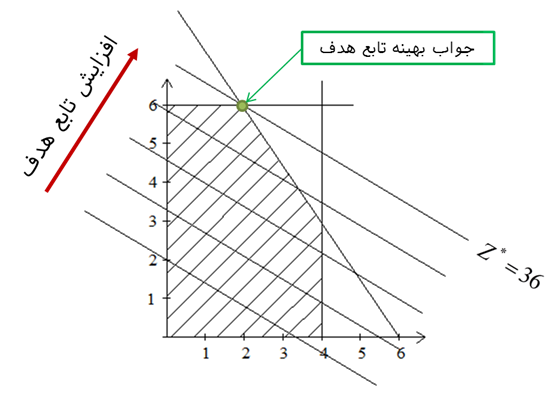
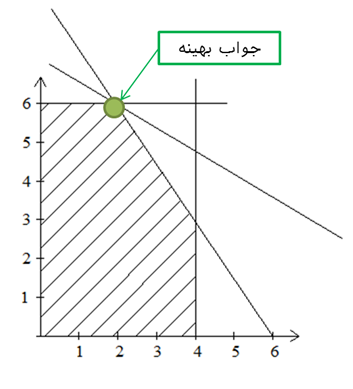
از رسم 3x₁ + 5x₂ = 10 بر روی ناحیه امکان پذیر می‌توان ملاحظه کرد که تعداد زیادی از نقاط محدوده امکان پذیر روی این خط قرار می‌گیرند. با افزایش مقدار 10 به 20 خواهیم دهید که باز هم بخشی از خط 3x₁ + 5x₂ = 20 در داخل ناحیه امکان پذیر قرار می‌گیرد. به این ترتیب با افزایش مقدار ثابت خط، مجموعه‌ای از خصوص موازی رسم می‌شوند. در نهایت خطی انتخاب می‌شود که بیشترین اختلاف را با مرکز مختصات دارد. همان طور که در شکل زیر پیداست، نقطه (2,6) از خط 3x₁ + 5x₂ = 36 می‌گذرد. این نقطه ( x₁ =2 و x₂ = 6 ) بیشترین عایدی را برای کارگاه ایجاد می نماید. لذا با تولید 2 واحد از محصول 1 و 6 واحد از محصول 2، بیشترین عایدی (z = 36) در دقیقه ایجاد می‌شود.

بیان ریاضی مدل برنامه ریزی خطی

در این بخش می‌توان مسئله شرکت تولید درب و پنجره را تعمیم داد. در این مسئله 3 کارگاه یا منبع با محدودیت ظرفیتی وجود دارند که باید دو محصول با توجه به نیازشان از این سه منبع استفاده کنند. اکنون فرض کنند m منبع را می خواهیم به n محصول رقیب تخصیص دهیم. فرض کنید که x_j حجم محصول j که و z معیار کارآمدی کلیه محصول‌های تولید شده است. همچنین فرض کنید تغییر کارآمدی یا z در اثر هر واحد افزایش (x_j (j=1,…,n باشد. همچنین b_i نشان دهنده مقدار موجود منبع (i ( i=1,…,m و بالاخره a_ij نشانگر مقداری از منبع i است که توسط محصول j مصرف می‌شود. خلاصه اطلاعات در جدول زیر آمده است.

با توجه به جدول بالا می‌توان فرم کلی مسئله تخصیص منابع را به زبان ریاضی به صورت زیر بیان کرد:

مدل فوق شکل استاندارد مسئله برنامه‌ریزی خطی می نامیم. هر مسئله‌ای که به شکل فوق باشد یک مسئله برنامه‌ریزی خطی است.

توجه : این شکل استاندارد در ادامه مورد استفاده قرار می‌گیرد و در سایر منابع شکل‌های دیگری به عنوان فرم استاندارد تعریف می‌شود.

واژه‌های مربوط به مدل برنامه‌ریزی خطی

برای سادگی در بیان مسائل در برنامه‌ریزی خطی، واژگان متداول به صورت زیر تعریف می‌شود.

تابع هدف (objective function): به تابع c₁x₁+c₂x₂+ … +c_nx_n که پیدا کردن حداکثر آن مورد نظر است اطلاق می‌شود.

محدودیت کارکردی(functional constraint): به تابعی که نشان دهنده میزان کل مصرف هر منبع برای کلیه محصول ها است اطلاق می‌شود.

محدودیت نامنفی بودن (non-negativity constraint): به روابط x_j ≥0 اطلاق می‌شود.

محدودیت‌ها(constraints): به مجموعه محدودیت‌های کارکردی و نامنفی بودن اطلاق می‌شود.

متغیرهای تصمیم(decision variables): به متغیرهای x_j که میزان هر محصول را نشان می‌دهد اطلاق می‌شود.

پارامترها(parameters): به داده‌های a_ij ، c_j ، b_i و اطلاق می‌شود.

نکته : ممکن است مدل استاندارد با بسیاری از مدل‌های برنامه‌ریزی خطی در واقعیت تفاوت داشته باشد. شکل‌های مجاز دیگر از مسئله برنامه‌ریزی خطی که امکان تبدیل به شکل استاندارد را دارد به صورت زیر است:

– ممکن است به جای حداکثر کردن (Max)، حداقل کردن (Min) در نظر باشد.

– ممکن است برخی از محدودیت‌های کارکردی به صورت بزرگتر –مساوی باشند.

a_i1x₁+a_i2x₂+ … +a_inx_n ≥ b_i

– ممکن است برخی از محدودیت‌های کارکردی به صورت تساوی باشند.

a_i1x₁+a_i2x₂+ … +a_inx_n = b_i

– ممکن است برخی از متغیرهای بتوانند فقط منفی یا هم منفی یا مثبت (آزاد در علامت یا unrestricted in sign) باشند.

واژه‌های مربوط به جواب‌های مدل

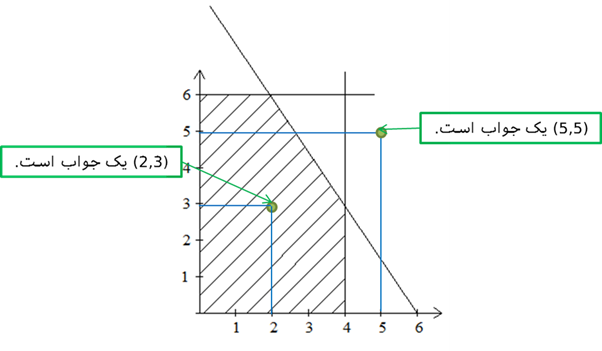
جواب (solution) : به هر مجموعه از مقادیر که به متغیرهای تصمیم (x_n,…,x₂,x₁) اختصاص یابد، اطلاق می‌شود. برای مثال در شکل مثال قبلی، نقطه (2,3) و (5,5) جواب‌های مدل برنامه‌ریزی خطی هستند و این که در داخل یا خارج محدودیت باشند اهمیت ندارد.

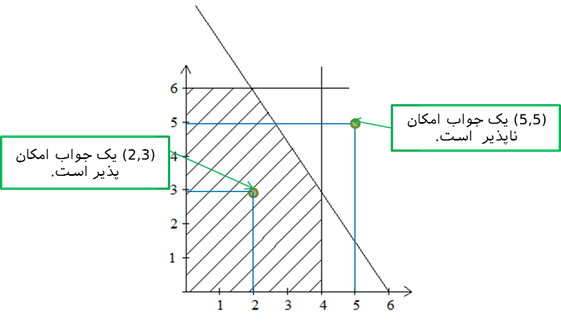
جواب موجه یا امکان پذیر (feasible solution): به جوابی که در تمامی محدودیت‌ها (عملکردی و نامنفی بودن) صدق می نماید، اطلاق می‌شود. برای مثال در شکل ذیل، نقطه (2,3) جواب موجه و جواب (5,5) یک جواب امکان ناپذیر است.

جواب بهینه (optimal solution): جوابی موجه است که به ازای آن (جواب بهینه)، مقدار تابع هدف مطلوب‌ترین است. در شکل زیر جواب بهینه مثال قبلی آورده شده است.

برای جواب بهینه چهار امکان وجود دارد:

1- جواب بهینه یکتا: در این صورت جواب بهینه تنها یک نقطه از فضای امکان پذیر است(مشابه شکل فوق).

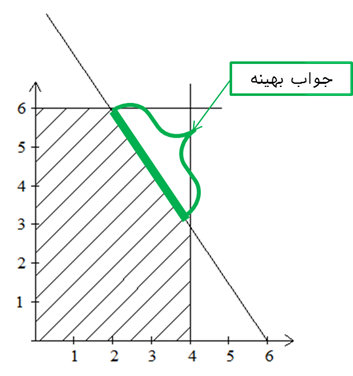
2- جواب بهینه چندگانه (multiple optimal solution): غالبا مسئله برنامه‌ریزی خطی یک جواب یکتا دارد. ولی لزوما این چنین نیست. در مثال قبلی اگر سودآوری محصول شماره 2 از 5 به 2 واحد کاهش یابد، در این صورت خط تابع هدف به موازات خط 3x₁ + 2x₂ = 18 خواهد شد و از این رو تمامی نقاط روی خط 3x₁ + 2x₂ = 18 بین نقاط (2,6) و (4,3) جواب‌های بهینه مسئله خواهد بود.

3- جواب بیکران (unbound solution): این جواب زمانی به وجود می آید که محدودیت‌ها نتوانند از افزایش لایتناهی تابع هدف (z) در جهت مطلوب جلوگیری نماید. در مثال قبلی اگر دو محدودیت 2x₂ ≤ 18 و 3x₁ + 2x₂ ≤ 18 حذف شوند، فضای امکان پذیر به صورت زیر می‌شود که مقدار تابع هدف می‌تواند در جهت لایتناهی افزایش یابد.

4- فاقد جواب (infeasible solution): در این صورت مسئله اصولا جواب موجه ندارد. اگر در مثال قبلی، محدودیت 2x₂ ≤ 12 به 2x₂ ≥ 12 و محدودیت x₁ ≤ 4 به x₂≥ 4 تغییر نماید، فضای امکان پذیر تهی می‌شود و مسئله فاقد جواب خواهد شد.